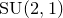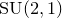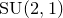1. Introduction
Let
![]() $\Gamma$
be the fundamental group of the one
$\Gamma$
be the fundamental group of the one
![]() $1$
-holed torus
$1$
-holed torus
![]() $S_{1,1}$
, that is,
$S_{1,1}$
, that is,
![]() $\Gamma \cong F_2 =\langle \alpha, \beta \rangle$
, a free group of rank
$\Gamma \cong F_2 =\langle \alpha, \beta \rangle$
, a free group of rank
![]() $2$
. The Lie group
$2$
. The Lie group
![]() $\mathrm {SU}(2,1)$
acts on the space of group homomorphisms
$\mathrm {SU}(2,1)$
acts on the space of group homomorphisms
![]() $\mathrm {Hom}(F_2,\mathrm {SU}(2,1))$
by conjugation. Let
$\mathrm {Hom}(F_2,\mathrm {SU}(2,1))$
by conjugation. Let
![]() $\mathrm {Hom}(F_2,\mathrm {SU}(2,1))^*$
be the subspace of
$\mathrm {Hom}(F_2,\mathrm {SU}(2,1))^*$
be the subspace of
![]() $\mathrm {Hom}(F_2,\mathrm {SU}(2,1))$
consisting of homomorphisms having closed conjugation orbits, and define the
$\mathrm {Hom}(F_2,\mathrm {SU}(2,1))$
consisting of homomorphisms having closed conjugation orbits, and define the
![]() $\mathrm {SU}(2,1)$
-character variety of
$\mathrm {SU}(2,1)$
-character variety of
![]() $F_2$
to be the quotient space
$F_2$
to be the quotient space
![]() $\mathfrak {X} = \mathrm {Hom}(F_2, \mathrm {SU}(2,1))^*/\mathrm {SU}(2,1)$
. The mapping class group
$\mathfrak {X} = \mathrm {Hom}(F_2, \mathrm {SU}(2,1))^*/\mathrm {SU}(2,1)$
. The mapping class group
![]() $\mathcal {MCG}(S_{1,1})$
is isomorphic to the outer automorphisms of
$\mathcal {MCG}(S_{1,1})$
is isomorphic to the outer automorphisms of
![]() $\Gamma$
and acts on
$\Gamma$
and acts on
![]() $\mathfrak {X}$
by pre-composition.
$\mathfrak {X}$
by pre-composition.
The main result of this paper is the following.
Theorem A.
There exists an open domain of discontinuity
![]() $\mathfrak {X}_{BQ}$
for the action of the mapping class group
$\mathfrak {X}_{BQ}$
for the action of the mapping class group
![]() $\mathcal {MCG}(S_{1,1})$
on
$\mathcal {MCG}(S_{1,1})$
on
![]() $\mathfrak {X}$
which strictly contains the set of discrete, faithful, convex cocompact representations.
$\mathfrak {X}$
which strictly contains the set of discrete, faithful, convex cocompact representations.
To prove this theorem we combine ideas of Bowditch [Reference BowditchBow98] (further generalized by Tan, Wong and Zhang [Reference Tan, Wong and ZhangTWZ08], Maloni, Palesi and Tan [Reference Maloni, Palesi and TanMPT15] and Maloni and Palesi [Reference Maloni and PalesiMP20]) with the explicit parametrization of the
![]() $\mathrm {SL}(3,\mathbb {C})$
-character variety of
$\mathrm {SL}(3,\mathbb {C})$
-character variety of
![]() $F_2$
described by Lawton [Reference LawtonLaw06, Reference LawtonLaw07]. In order to describe the set of representations that form
$F_2$
described by Lawton [Reference LawtonLaw06, Reference LawtonLaw07]. In order to describe the set of representations that form
![]() $\mathfrak {X}_{BQ}$
, called Bowditch representations, we need to analyze what are called ‘relative character varieties’. Given
$\mathfrak {X}_{BQ}$
, called Bowditch representations, we need to analyze what are called ‘relative character varieties’. Given
![]() $c \in \mathbb {C}$
, we define the relative character variety
$c \in \mathbb {C}$
, we define the relative character variety
![]() $\mathfrak {X}_c$
to be the set of
$\mathfrak {X}_c$
to be the set of
![]() $\mathrm {SU}(2,1)$
-valued representations of
$\mathrm {SU}(2,1)$
-valued representations of
![]() $\Gamma$
with fixed trace of the peripheral element
$\Gamma$
with fixed trace of the peripheral element
![]() $[\alpha, \beta ]$
:
$[\alpha, \beta ]$
:
As a bi-product of our work, we can show that Bowditch representations can be defined in many equivalent ways. For an isometry
![]() $\varphi$
of complex hyperbolic space
$\varphi$
of complex hyperbolic space
![]() $ \mathbf {H}_{\mathbb {C}}^2$
, define
$ \mathbf {H}_{\mathbb {C}}^2$
, define
![]() $l(\varphi )$
as follows:
$l(\varphi )$
as follows:
Let
![]() $\mathcal {S}$
be the set of free homotopy classes of essential unoriented simple closed curves on
$\mathcal {S}$
be the set of free homotopy classes of essential unoriented simple closed curves on
![]() $S_{1,1}$
. We can define the following properties for representations in
$S_{1,1}$
. We can define the following properties for representations in
![]() $\mathfrak {X}_c$
:
$\mathfrak {X}_c$
:
-
(BQ1)
 $\forall \gamma \in \mathcal {S}$
,
$\forall \gamma \in \mathcal {S}$
,
 $f(\textrm {tr }\rho (\gamma )) \gt 0$
(equivalently
$f(\textrm {tr }\rho (\gamma )) \gt 0$
(equivalently
 $\rho (\gamma )$
is loxodromic), where
$\rho (\gamma )$
is loxodromic), where \begin{equation*}f(t)=|t|^4 - 8 \Re (t^3)+18 |t|^2 - 27;\end{equation*}
\begin{equation*}f(t)=|t|^4 - 8 \Re (t^3)+18 |t|^2 - 27;\end{equation*}
-
(BQ2)
 $\#\{\gamma \in \mathcal {S} \mid |\textrm {tr }\rho (\gamma )| \leqslant M(c) \} \lt \infty$
, where
$\#\{\gamma \in \mathcal {S} \mid |\textrm {tr }\rho (\gamma )| \leqslant M(c) \} \lt \infty$
, where
 $M(c)\gt 0$
is defined in Section 3.4;
$M(c)\gt 0$
is defined in Section 3.4; -
(BQ2’)
 $ \forall K\gt 0$
,
$ \forall K\gt 0$
,
 $\; \#\{\gamma \in \mathcal {S} \mid |\textrm {tr }\rho (\gamma )| \leqslant K\} \lt \infty .$
$\; \#\{\gamma \in \mathcal {S} \mid |\textrm {tr }\rho (\gamma )| \leqslant K\} \lt \infty .$
-
(BQ3) there exists
 $k, m \gt 0$
such that
$k, m \gt 0$
such that
 $|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
$|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
 $\gamma \in \mathcal {S}$
;
$\gamma \in \mathcal {S}$
; -
(BQ4)
 $\forall K\geqslant M(c)$
, the attracting subgraph
$\forall K\geqslant M(c)$
, the attracting subgraph
 $T_\rho (K)$
(defined in Section 3.5) is finite.
$T_\rho (K)$
(defined in Section 3.5) is finite.
In Section 4.3 we prove the following result.
Theorem B.
Let
![]() $[\rho ]\in \mathfrak {X}_c$
. The following are equivalent:
$[\rho ]\in \mathfrak {X}_c$
. The following are equivalent:
-
(i) the representation
 $\rho$
satisfies
$\rho$
satisfies
 $(BQ1)$
and
$(BQ1)$
and
 $(BQ2)$
;
$(BQ2)$
; -
(ii) the representation
 $\rho$
satisfies
$\rho$
satisfies
 $(BQ1)$
and
$(BQ1)$
and
 $(BQ2')$
;
$(BQ2')$
; -
(iii) the representation
 $\rho$
satisfies
$\rho$
satisfies
 $(BQ3)$
;
$(BQ3)$
; -
(iv) the representation
 $\rho$
satisfies
$\rho$
satisfies
 $(BQ4)$
.
$(BQ4)$
.
So the set of Bowditch representations
![]() $\mathfrak {X}_{BQ}$
referred to in TheoremA is the union over
$\mathfrak {X}_{BQ}$
referred to in TheoremA is the union over
![]() $c\in \mathbb {C}$
of the Bowditch representations in
$c\in \mathbb {C}$
of the Bowditch representations in
![]() $\mathfrak {X}_c$
defined by any of the equivalent conditions in TheoremB. A corollary of the above theorem, given the work of [Reference SchlichSch22], is that our set
$\mathfrak {X}_c$
defined by any of the equivalent conditions in TheoremB. A corollary of the above theorem, given the work of [Reference SchlichSch22], is that our set
![]() $\mathfrak {X}_{BQ}$
coincides with the set of ‘primitive-stable representations’ defined in [Reference Kim and KimKK20].
$\mathfrak {X}_{BQ}$
coincides with the set of ‘primitive-stable representations’ defined in [Reference Kim and KimKK20].
We also prove the somewhat surprising result that the topology of the character variety
![]() $\mathfrak {X}$
is non-trivial. In particular, we prove the following.
$\mathfrak {X}$
is non-trivial. In particular, we prove the following.
Theorem C.
The
![]() $\mathrm {SU}(2,1)$
-character variety of
$\mathrm {SU}(2,1)$
-character variety of
![]() $F_2$
$F_2$
![]() $\mathfrak {X}$
strong deformation retracts onto
$\mathfrak {X}$
strong deformation retracts onto
![]() $S^1\times S^1$
. In particular, it is not simply connected.
$S^1\times S^1$
. In particular, it is not simply connected.
This is surprising because the
![]() $\mathrm {SU}(3)$
-character variety of
$\mathrm {SU}(3)$
-character variety of
![]() $F_2$
satisfies the same real algebraic equations and has the same (real) dimension, but it is not homeomorphic to
$F_2$
satisfies the same real algebraic equations and has the same (real) dimension, but it is not homeomorphic to
![]() $\mathfrak {X}$
, since the
$\mathfrak {X}$
, since the
![]() $\mathrm {SU}(3)$
-character variety of
$\mathrm {SU}(3)$
-character variety of
![]() $F_2$
is homeomorphic to an
$F_2$
is homeomorphic to an
![]() $8$
-sphere by Florentino and Lawton [Reference Florentino and LawtonFL09].
$8$
-sphere by Florentino and Lawton [Reference Florentino and LawtonFL09].
1.1 Proof strategy
We now give an overview of the proof of TheoremA and TheoremB. The proof can be organized into five main steps:
-
(0) description of the combinatorial setup:
 $\mathcal {C}, \mathcal {T},\mathcal {E}$
;
$\mathcal {C}, \mathcal {T},\mathcal {E}$
; -
(1) orientation on
 $\mathcal {E}$
, fork lemma and connectivity of the regions
$\mathcal {E}$
, fork lemma and connectivity of the regions
 $\Sigma$
;
$\Sigma$
; -
(2) growth of traces for neighbors around a region and for escaping rays, and definition of an attracting subgraph of
 $\mathcal {E}$
;
$\mathcal {E}$
; -
(3) Fibonacci growth and equivalent characterizations of Bowditch representations;
-
(4) proof that the set
 $\mathfrak {X}_{BQ}$
strictly contains convex cocompact representations.
$\mathfrak {X}_{BQ}$
strictly contains convex cocompact representations.
-
Step (0): We start with a discussion of the combinatorial setup needed for our study. Given the one-hole torus
 $S:=S_{1,1}$
, we define three simplicial complexes associated to
$S:=S_{1,1}$
, we define three simplicial complexes associated to
 $S$
: the curve complex
$S$
: the curve complex
 $\mathcal {C}$
, its dual
$\mathcal {C}$
, its dual
 $\mathcal {T}$
and the edge graph
$\mathcal {T}$
and the edge graph
 $\mathcal {E}$
. The curve complex
$\mathcal {E}$
. The curve complex
 $\mathcal {C}$
is the two-dimensional simplicial complex, where
$\mathcal {C}$
is the two-dimensional simplicial complex, where
 $k$
-simplices are given by
$k$
-simplices are given by
 $k+1$
distinct (free homotopy classes of) simple closed curves in
$k+1$
distinct (free homotopy classes of) simple closed curves in
 $S$
that pairwise intersect once. Its simplicial dual
$S$
that pairwise intersect once. Its simplicial dual
 $\mathcal {T}$
is a countably infinite tri-valent simplicial tree properly embedded in
$\mathcal {T}$
is a countably infinite tri-valent simplicial tree properly embedded in
 $\mathbf {H}^2$
defined by the property that the set
$\mathbf {H}^2$
defined by the property that the set
 $\mathcal {T}^{(k)}$
of
$\mathcal {T}^{(k)}$
of
 $k$
-simplices in
$k$
-simplices in
 $\mathcal {T}$
satisfies
$\mathcal {T}$
satisfies
 $\mathcal {T}^{(k)} = \mathcal {C}^{(2-k)}$
for
$\mathcal {T}^{(k)} = \mathcal {C}^{(2-k)}$
for
 $k=0,1,2$
. Finally, the edge graph
$k=0,1,2$
. Finally, the edge graph
 $\mathcal {E}$
has vertices corresponding to edges of
$\mathcal {E}$
has vertices corresponding to edges of
 $\mathcal {T}$
, and edges corresponding to adjacency, so one can see that
$\mathcal {T}$
, and edges corresponding to adjacency, so one can see that
 $\mathcal {E}$
is a ‘trivalent tree of triangles’ in the sense that it is a graph made of triangles (one for each triangle
$\mathcal {E}$
is a ‘trivalent tree of triangles’ in the sense that it is a graph made of triangles (one for each triangle
 $T$
in
$T$
in
 $\mathcal {C}^{(2)}$
or, equivalently, one for each vertex of
$\mathcal {C}^{(2)}$
or, equivalently, one for each vertex of
 $\mathcal T$
). See Figure 1.
$\mathcal T$
). See Figure 1. -
Step (1): For the first step, we show how any representation in
 $\mathfrak {X}_c$
induces an orientation on the edges of
$\mathfrak {X}_c$
induces an orientation on the edges of
 $\mathcal {E}$
as follows. An edge
$\mathcal {E}$
as follows. An edge
 $(X, Y, Z; T, T) \in \mathcal {E}$
indicates that the edge is in the triangle
$(X, Y, Z; T, T) \in \mathcal {E}$
indicates that the edge is in the triangle
 $(X, Y, Z) \in \mathcal {C}^2$
and is between the triangles
$(X, Y, Z) \in \mathcal {C}^2$
and is between the triangles
 $(X, Y, T), (X, Z, T') \in \mathcal {C}^2$
which are adjacent to
$(X, Y, T), (X, Z, T') \in \mathcal {C}^2$
which are adjacent to
 $(X, Y, Z)$
, see Figure 2. If
$(X, Y, Z)$
, see Figure 2. If
 $t = |\mathrm {tr} (\rho (T)) | \gt |\mathrm {tr} (\rho (T'))| = t'$
, then the oriented edge points towards
$t = |\mathrm {tr} (\rho (T)) | \gt |\mathrm {tr} (\rho (T'))| = t'$
, then the oriented edge points towards
 $T'$
. In the case where there is an equality, one can choose the orientation arbitrarily (and the choice will not affect the result).
$T'$
. In the case where there is an equality, one can choose the orientation arbitrarily (and the choice will not affect the result).We have a
 $4$
-coloring of the edges of
$4$
-coloring of the edges of
 $\mathcal {E}$
such that at each vertex there are only two triangles of two different colors meeting. We say that a vertex
$\mathcal {E}$
such that at each vertex there are only two triangles of two different colors meeting. We say that a vertex
 $v \in \mathcal {E}^{(0)}$
is a fork if there are (at least) two arrows of different colors pointing away from
$v \in \mathcal {E}^{(0)}$
is a fork if there are (at least) two arrows of different colors pointing away from
 $v$
. The Fork Lemma (Lemma3.4) shows that if a vertex
$v$
. The Fork Lemma (Lemma3.4) shows that if a vertex
 $v = (X, Y) \in \mathcal {E}^{(0)}$
is a fork, then
$v = (X, Y) \in \mathcal {E}^{(0)}$
is a fork, then
 $\min \{|x|, |y| \} \leqslant \max \{6,\sqrt {|\Re (c)|}\}$
for
$\min \{|x|, |y| \} \leqslant \max \{6,\sqrt {|\Re (c)|}\}$
for
 $x=\textrm {tr }(\rho (X))$
and
$x=\textrm {tr }(\rho (X))$
and
 $y=\textrm {tr }(\rho (Y))$
. We use this result to show, for
$y=\textrm {tr }(\rho (Y))$
. We use this result to show, for
 $[\rho ] \in \mathfrak {X}_c$
, the set
$[\rho ] \in \mathfrak {X}_c$
, the set
 $\Omega _\rho (K)$
of regions with traces smaller than
$\Omega _\rho (K)$
of regions with traces smaller than
 $K \geqslant \max \{6,\sqrt {|\Re (c)|}\}$
is connected. The proof is by contradiction and considers the distance between two connected components. The Fork Lemma is used to reach the conclusion when such a distance is greater than
$K \geqslant \max \{6,\sqrt {|\Re (c)|}\}$
is connected. The proof is by contradiction and considers the distance between two connected components. The Fork Lemma is used to reach the conclusion when such a distance is greater than
 $2$
since in that case a fork will appear.
$2$
since in that case a fork will appear. -
Step (2): For the second step we first study the behavior of the values of the (norm of the) traces of regions that are all neighbors of a central region
 $X$
. Given
$X$
. Given
 $[\rho ] \in \mathfrak {X}_c$
we see that if we denote by
$[\rho ] \in \mathfrak {X}_c$
we see that if we denote by
 $(X_n)_{n \in \mathbb {Z}}$
the regions around
$(X_n)_{n \in \mathbb {Z}}$
the regions around
 $X$
, then the behavior of the sequence
$X$
, then the behavior of the sequence
 $(u_n)_{n\in \mathbb {N}}$
defined by
$(u_n)_{n\in \mathbb {N}}$
defined by
 $u_n = \mathrm {tr} (\rho (X_n))$
depends on the value of
$u_n = \mathrm {tr} (\rho (X_n))$
depends on the value of
 $f(x)$
where
$f(x)$
where
 $x=\textrm {tr }(\rho (X))$
and
$x=\textrm {tr }(\rho (X))$
and
 $f(x) = \mathrm {Res} (\chi _x, \chi _x')$
. In fact if
$f(x) = \mathrm {Res} (\chi _x, \chi _x')$
. In fact if
 $f(x)=0$
, then
$f(x)=0$
, then
 $(u_n)_{n\in \mathbb {N}}$
grows at most quadratically, while if
$(u_n)_{n\in \mathbb {N}}$
grows at most quadratically, while if
 $f(x) \lt 0$
, then
$f(x) \lt 0$
, then
 $(u_n)_{n\in \mathbb {N}}$
remains bounded. Finally, in Lemma3.8 we show that there exists a constant
$(u_n)_{n\in \mathbb {N}}$
remains bounded. Finally, in Lemma3.8 we show that there exists a constant
 $D = D(c)$
, such that if the sequence
$D = D(c)$
, such that if the sequence
 $(u_n)_{n\in \mathbb {N}}$
defined above with
$(u_n)_{n\in \mathbb {N}}$
defined above with
 $f(x) \gt 0$
does not grow exponentially in both directions, then there are infinitely many terms of the sequence such that
$f(x) \gt 0$
does not grow exponentially in both directions, then there are infinitely many terms of the sequence such that
 $|u_n| \lt D$
. We then consider escaping rays, that is infinite geodesic rays where each edge
$|u_n| \lt D$
. We then consider escaping rays, that is infinite geodesic rays where each edge
 $e_n$
is directed from
$e_n$
is directed from
 $v_n$
to
$v_n$
to
 $v_{n+1}$
. In Lemma3.11 we show that if
$v_{n+1}$
. In Lemma3.11 we show that if
 $\{ e_n \}_{n\in \mathbb {N}}$
is an escaping ray, then there are two cases:
$\{ e_n \}_{n\in \mathbb {N}}$
is an escaping ray, then there are two cases:-
(1) there exists a region
 $\alpha$
such that the ray is eventually contained in the boundary of
$\alpha$
such that the ray is eventually contained in the boundary of
 $\alpha$
, such that
$\alpha$
, such that
 $f(x) \leqslant 0$
with
$f(x) \leqslant 0$
with
 $x = \mathrm {tr} (\rho (\alpha ))$
; or
$x = \mathrm {tr} (\rho (\alpha ))$
; or -
(2) the ray meets infinitely many distinct regions with trace smaller than
 $M(c)$
, where
$M(c)$
, where
 $M(c):=\max \{6, \sqrt {|\Re (c)|}, D(c)\}$
.
$M(c):=\max \{6, \sqrt {|\Re (c)|}, D(c)\}$
.
Using the description of the growth of the traces for regions around a fixed central trace, we define, for every representation
 $[\rho ] \in \mathfrak {X}_c$
and for every
$[\rho ] \in \mathfrak {X}_c$
and for every
 $K\gt M(c)$
, a connected attracting subgraph
$K\gt M(c)$
, a connected attracting subgraph
 $T_\rho (K)$
of
$T_\rho (K)$
of
 $\mathcal {E}$
. (Recall that
$\mathcal {E}$
. (Recall that
 $\mathcal {E}$
is a ‘trivalent tree of triangles’, so we want to define
$\mathcal {E}$
is a ‘trivalent tree of triangles’, so we want to define
 $T_\rho (K)$
so that it is a union of ‘triangles’.) The connectivity of
$T_\rho (K)$
so that it is a union of ‘triangles’.) The connectivity of
 $T_\rho (K)$
comes from the connectivity of
$T_\rho (K)$
comes from the connectivity of
 $\Omega _\rho (K)$
, while the fact that
$\Omega _\rho (K)$
, while the fact that
 $T_\rho (K)$
is attractive comes from the definition of
$T_\rho (K)$
is attractive comes from the definition of
 $T_\rho (K)$
. We then show that for representations in
$T_\rho (K)$
. We then show that for representations in
 $\mathfrak {X}_{BQ}$
, that is representations satisfying conditions (BQ1) and (BQ2), such a graph
$\mathfrak {X}_{BQ}$
, that is representations satisfying conditions (BQ1) and (BQ2), such a graph
 $T_\rho (K)$
is finite for all
$T_\rho (K)$
is finite for all
 $K\gt M(c)$
.
$K\gt M(c)$
. -
-
Step (3): In the penultimate step, given a vertex
 $v \in \mathcal {E}^{(0)}$
, we define a Fibonacci function
$v \in \mathcal {E}^{(0)}$
, we define a Fibonacci function
 $F_v : \Omega \rightarrow \mathbb {N}$
. We then show that this function has the following property: if
$F_v : \Omega \rightarrow \mathbb {N}$
. We then show that this function has the following property: if
 $\{\alpha, \beta \}$
is a set of free generators for
$\{\alpha, \beta \}$
is a set of free generators for
 $F_2$
corresponding to regions
$F_2$
corresponding to regions
 $X$
and
$X$
and
 $Y$
such that
$Y$
such that
 $v =(X, Y) \in \mathcal {E}^{(0)}$
, then for any element
$v =(X, Y) \in \mathcal {E}^{(0)}$
, then for any element
 $\gamma \in \Omega$
the Fibonacci function corresponds to the word length of
$\gamma \in \Omega$
the Fibonacci function corresponds to the word length of
 $\gamma$
with respect to
$\gamma$
with respect to
 $\{\alpha, \beta \}$
, that is
$\{\alpha, \beta \}$
, that is
 $F_v(\gamma ) = W(\gamma )$
. Note that we only care about the asymptotic growth of this function, as you will see, so the choice of
$F_v(\gamma ) = W(\gamma )$
. Note that we only care about the asymptotic growth of this function, as you will see, so the choice of
 $v$
will not affect our results. We then define what it means for a function
$v$
will not affect our results. We then define what it means for a function
 $g \colon \thinspace \Omega \rightarrow [0, \infty )$
to have Fibonacci growth, i.e. there exist constants
$g \colon \thinspace \Omega \rightarrow [0, \infty )$
to have Fibonacci growth, i.e. there exist constants
 $\kappa _1, \kappa _2 \gt 0$
such thatfor all
$\kappa _1, \kappa _2 \gt 0$
such thatfor all \begin{equation*}\kappa _1 F_v (X) \leqslant g(X) \leqslant \kappa _2 F_v (X)\end{equation*}
\begin{equation*}\kappa _1 F_v (X) \leqslant g(X) \leqslant \kappa _2 F_v (X)\end{equation*}
 $X \in \Omega$
. If only the lower (respectively, upper) bound is satisfied, the function
$X \in \Omega$
. If only the lower (respectively, upper) bound is satisfied, the function
 $g$
is said to have a lower (respectively, upper) Fibonacci growth. Given any
$g$
is said to have a lower (respectively, upper) Fibonacci growth. Given any
 $[\rho ] \in \mathfrak {X}$
, we denote by
$[\rho ] \in \mathfrak {X}$
, we denote by
 $\phi _\rho \colon \thinspace \Omega \rightarrow \mathbb {C}$
the function
$\phi _\rho \colon \thinspace \Omega \rightarrow \mathbb {C}$
the function
 $\phi _\rho (X) := \log | \mathrm {tr} (\rho (X)) |$
. We consider the function
$\phi _\rho (X) := \log | \mathrm {tr} (\rho (X)) |$
. We consider the function
 $\phi _\rho ^+ := \max \{ \phi _\rho, 0 \}$
. We then show that this function always has an upper Fibonacci growth, but for representations in
$\phi _\rho ^+ := \max \{ \phi _\rho, 0 \}$
. We then show that this function always has an upper Fibonacci growth, but for representations in
 $[\rho ] \in \mathfrak {X}_{BQ}$
we show that the function has upper and lower Fibonacci growth.
$[\rho ] \in \mathfrak {X}_{BQ}$
we show that the function has upper and lower Fibonacci growth.
We use this result to show that we can characterize representations in
 $\mathfrak {X}_{BQ}$
in terms of the attracting graph
$\mathfrak {X}_{BQ}$
in terms of the attracting graph
 $T_\rho (K)$
as follows:
$T_\rho (K)$
as follows:
 $[\rho ]$
is in
$[\rho ]$
is in
 $(\mathfrak {X}_c)_{BQ}$
if and only if the subgraph
$(\mathfrak {X}_c)_{BQ}$
if and only if the subgraph
 $T_\rho (K)$
is finite for all
$T_\rho (K)$
is finite for all
 $K\gt M(c)$
, which proves TheoremB. This result is crucial to show that the set
$K\gt M(c)$
, which proves TheoremB. This result is crucial to show that the set
 $\mathfrak {X}_{BQ}$
is open and the mapping class group acts on it properly discontinuously, and hence to prove TheoremA.
$\mathfrak {X}_{BQ}$
is open and the mapping class group acts on it properly discontinuously, and hence to prove TheoremA. -
Step (4): In order to show that the set
 $\mathfrak {X}_{BQ}$
strictly contains convex cocompact representations, we use representations described by Will [Reference WillWil07, Reference WillWil12]: a family of discrete, faithful and type-preserving representations of the once-punctured torus in
$\mathfrak {X}_{BQ}$
strictly contains convex cocompact representations, we use representations described by Will [Reference WillWil07, Reference WillWil12]: a family of discrete, faithful and type-preserving representations of the once-punctured torus in
 $\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. These representations will take non-peripheral, non-trivial simple closed curves to loxodromic elements and will map the commutator to a parabolic unipotent element. In order to see that these representations are in
$\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. These representations will take non-peripheral, non-trivial simple closed curves to loxodromic elements and will map the commutator to a parabolic unipotent element. In order to see that these representations are in
 $\mathfrak {X}_{BQ}$
, we use a characterization of both sets in term of the growth of
$\mathfrak {X}_{BQ}$
, we use a characterization of both sets in term of the growth of
 $|l (\rho (\gamma ))|$
: the existence of
$|l (\rho (\gamma ))|$
: the existence of
 $k, m \gt 0$
such that
$k, m \gt 0$
such that
 $|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
$|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
 $\gamma \in F_2$
corresponding to non-peripheral, non-trivial simple closed curves in
$\gamma \in F_2$
corresponding to non-peripheral, non-trivial simple closed curves in
 $S_{1,1}$
. On the other hand, since the (peripheral) simple closed curve corresponding to the commutator is mapped to a unipotent element, we can see these representations are not convex cocompact. There are also other examples of representations that are in
$S_{1,1}$
. On the other hand, since the (peripheral) simple closed curve corresponding to the commutator is mapped to a unipotent element, we can see these representations are not convex cocompact. There are also other examples of representations that are in
 $\mathfrak {X}_{BQ} \setminus \mathfrak {X}_{CC}$
and such that the peripheral element is mapped to a parabolic non-unipotent element, see Falbel and Parker [Reference Falbel and ParkerFP03], Falbel and Koseleff [Reference Falbel and KoseleffFK02b, Reference Falbel and KoseleffFK02a] or Parker and Gusevskii [Reference Gusevskii and ParkerGP03, Reference Gusevskii and ParkerGP00]. See Will [Reference WillWil16] for a discussion of these references.
$\mathfrak {X}_{BQ} \setminus \mathfrak {X}_{CC}$
and such that the peripheral element is mapped to a parabolic non-unipotent element, see Falbel and Parker [Reference Falbel and ParkerFP03], Falbel and Koseleff [Reference Falbel and KoseleffFK02b, Reference Falbel and KoseleffFK02a] or Parker and Gusevskii [Reference Gusevskii and ParkerGP03, Reference Gusevskii and ParkerGP00]. See Will [Reference WillWil16] for a discussion of these references.

Figure 1. The complexes
![]() $\mathcal {C}$
(in gray) and
$\mathcal {C}$
(in gray) and
![]() $\mathcal {T}$
(in black), and the labeling of the connected components of
$\mathcal {T}$
(in black), and the labeling of the connected components of
![]() $\mathbf {H}^2 \setminus \mathcal {T}$
once we fix the generators of
$\mathbf {H}^2 \setminus \mathcal {T}$
once we fix the generators of
![]() $F_2 = \langle \alpha, \beta \rangle$
.
$F_2 = \langle \alpha, \beta \rangle$
.

Figure 2. Oriented edge
![]() $(X, Y, Z; T \longrightarrow T')$
. If you forget the orientation, the same red edge can be denoted
$(X, Y, Z; T \longrightarrow T')$
. If you forget the orientation, the same red edge can be denoted
![]() $(X; Y, Z)$
.
$(X; Y, Z)$
.
1.2 General setting
Let
![]() $\Gamma$
be a finitely presentable group with the discrete topology and let
$\Gamma$
be a finitely presentable group with the discrete topology and let
![]() $G$
be a Lie group. The set
$G$
be a Lie group. The set
![]() $\mathrm {Hom}(\Gamma, G)$
of homomorphisms from
$\mathrm {Hom}(\Gamma, G)$
of homomorphisms from
![]() $\Gamma$
to
$\Gamma$
to
![]() $G$
is a topological space by giving it the compact-open topology. The group
$G$
is a topological space by giving it the compact-open topology. The group
![]() $G$
acts on
$G$
acts on
![]() $\mathrm {Hom}(\Gamma, G)$
by conjugation, that is,
$\mathrm {Hom}(\Gamma, G)$
by conjugation, that is,
![]() $g\cdot \rho := \iota _g\circ \rho$
where
$g\cdot \rho := \iota _g\circ \rho$
where
![]() $\iota _g\in \mathrm {Inn}(G)$
. Let
$\iota _g\in \mathrm {Inn}(G)$
. Let
![]() $\mathrm {Orb}_G(\rho )$
be the
$\mathrm {Orb}_G(\rho )$
be the
![]() $G$
-orbit of
$G$
-orbit of
![]() $\rho$
. Define the subspace of polystable homomorphisms
$\rho$
. Define the subspace of polystable homomorphisms
and define the polystable quotient space
This quotient is called the
![]() $G$
-character variety of
$G$
-character variety of
![]() $\Gamma$
for historical reasons, even though in this generality it may be neither a variety, see Casimiro et al. [Reference Casimiro, Florentino, Lawton and OliveiraCFLO16], nor correspond to characters, see Lawton and Sikora [Reference Lawton and SikoraLS17].
$\Gamma$
for historical reasons, even though in this generality it may be neither a variety, see Casimiro et al. [Reference Casimiro, Florentino, Lawton and OliveiraCFLO16], nor correspond to characters, see Lawton and Sikora [Reference Lawton and SikoraLS17].
Let
![]() $\mathcal {P}$
be a collection of properties such that if
$\mathcal {P}$
be a collection of properties such that if
![]() $\rho \in \mathrm {Hom}(\Gamma, G)$
satisfies
$\rho \in \mathrm {Hom}(\Gamma, G)$
satisfies
![]() $\mathcal {P}$
, then
$\mathcal {P}$
, then
![]() $\iota _g\circ \rho$
also satisfies
$\iota _g\circ \rho$
also satisfies
![]() $\mathcal {P}$
for all
$\mathcal {P}$
for all
![]() $g\in G$
. Then
$g\in G$
. Then
![]() $G$
acts on the subspace
$G$
acts on the subspace
by conjugation. The polystable quotient of
![]() $\mathrm {Hom}_{\mathcal {P}}(\Gamma, G)$
by
$\mathrm {Hom}_{\mathcal {P}}(\Gamma, G)$
by
![]() $G$
, denoted by
$G$
, denoted by
![]() $\mathfrak {X}_{\mathcal {P}}(\Gamma, G)$
, is called the
$\mathfrak {X}_{\mathcal {P}}(\Gamma, G)$
, is called the
![]() $\mathcal {P}$
-relative
$\mathcal {P}$
-relative
![]() $G$
-character variety of
$G$
-character variety of
![]() $\Gamma$
. If
$\Gamma$
. If
![]() $\mathcal {P}$
is vacuous, one gets back
$\mathcal {P}$
is vacuous, one gets back
![]() $\mathfrak {X}(\Gamma, G).$
$\mathfrak {X}(\Gamma, G).$
Let
![]() $\mathrm {Aut}_{\mathcal {P}}(\Gamma )$
denote the subgroup of
$\mathrm {Aut}_{\mathcal {P}}(\Gamma )$
denote the subgroup of
![]() $\mathrm {Aut}(\Gamma )$
that preserves
$\mathrm {Aut}(\Gamma )$
that preserves
![]() $\mathrm {Hom}_{\mathcal {P}}(\Gamma, G)$
. Then
$\mathrm {Hom}_{\mathcal {P}}(\Gamma, G)$
. Then
![]() $\mathrm {Inn}(\Gamma )\subset \mathrm {Aut}_{\mathcal {P}}(\Gamma )$
and so
$\mathrm {Inn}(\Gamma )\subset \mathrm {Aut}_{\mathcal {P}}(\Gamma )$
and so
![]() $\mathrm {Out}_{\mathcal {P}}(\Gamma ):=\mathrm {Aut}_{\mathcal {P}}(\Gamma )/\mathrm {Inn}(\Gamma )$
acts on
$\mathrm {Out}_{\mathcal {P}}(\Gamma ):=\mathrm {Aut}_{\mathcal {P}}(\Gamma )/\mathrm {Inn}(\Gamma )$
acts on
![]() $\mathfrak {X}_{\mathcal {P}}(\Gamma, G)$
by
$\mathfrak {X}_{\mathcal {P}}(\Gamma, G)$
by
![]() $[\alpha ]\cdot [\rho ]=[\rho \circ \alpha ^{-1}]$
. Again, if
$[\alpha ]\cdot [\rho ]=[\rho \circ \alpha ^{-1}]$
. Again, if
![]() $\mathcal {P}=\emptyset$
, one obtains an action of
$\mathcal {P}=\emptyset$
, one obtains an action of
![]() $\mathrm {Out}(\Gamma )$
on
$\mathrm {Out}(\Gamma )$
on
![]() $\mathfrak {X}(\Gamma, G)$
.
$\mathfrak {X}(\Gamma, G)$
.
One of the main theorems in Rapinchuk [Reference RapinchukRap15] says that, for any complex affine variety
![]() $V$
, there exists a finitely generated group
$V$
, there exists a finitely generated group
![]() $\Gamma$
and a complex reductive group
$\Gamma$
and a complex reductive group
![]() $G$
, so that
$G$
, so that
![]() $\mathfrak {X}(\Gamma, G)-\{\chi _0\}$
and
$\mathfrak {X}(\Gamma, G)-\{\chi _0\}$
and
![]() $V$
are isomorphic where
$V$
are isomorphic where
![]() $\chi _0$
is the point in the character variety corresponding to the trivial representation. Let
$\chi _0$
is the point in the character variety corresponding to the trivial representation. Let
![]() $\mathcal {F}$
be the collection of finitely generated groups and
$\mathcal {F}$
be the collection of finitely generated groups and
![]() $\mathcal {G}$
the collection of complex reductive affine algebraic groups. Then, since the
$\mathcal {G}$
the collection of complex reductive affine algebraic groups. Then, since the
![]() $G$
-character variety of the trivial group
$G$
-character variety of the trivial group
![]() $\Gamma =\{e\}$
is a point for any
$\Gamma =\{e\}$
is a point for any
![]() $G$
, the set
$G$
, the set
![]() $\{\mathfrak {X}(\Gamma, G)\ |\ \Gamma \in \mathcal {F},\ G\in \mathcal {G}\}$
generates the Grothendieck ring of affine varieties. By Bumagin and Wise [Reference Bumagin and WiseBW05] all countable groups arise as
$\{\mathfrak {X}(\Gamma, G)\ |\ \Gamma \in \mathcal {F},\ G\in \mathcal {G}\}$
generates the Grothendieck ring of affine varieties. By Bumagin and Wise [Reference Bumagin and WiseBW05] all countable groups arise as
![]() $\mathrm {Out}(\Gamma )$
as we vary finitely generated
$\mathrm {Out}(\Gamma )$
as we vary finitely generated
![]() $\Gamma$
. So we have a very rich class of natural dynamical systems
$\Gamma$
. So we have a very rich class of natural dynamical systems
![]() $(\mathfrak {X}(\Gamma, G),\mathrm {Out}(\Gamma ))$
which are interesting only when both
$(\mathfrak {X}(\Gamma, G),\mathrm {Out}(\Gamma ))$
which are interesting only when both
![]() $\mathfrak {X}(\Gamma, G)$
and
$\mathfrak {X}(\Gamma, G)$
and
![]() $\mathrm {Out}(\Gamma )$
are non-trivial.
$\mathrm {Out}(\Gamma )$
are non-trivial.
1.3 Some history
A classical example to consider is when
![]() $G=\mathrm {U}(1)$
and
$G=\mathrm {U}(1)$
and
![]() $\Gamma =\Gamma _g$
is the fundamental group of a closed orientable surface
$\Gamma =\Gamma _g$
is the fundamental group of a closed orientable surface
![]() $S_g$
of genus
$S_g$
of genus
![]() $g$
. Then
$g$
. Then
![]() $\mathfrak {X}(\Gamma _g, G)=\mathrm {Hom}(\Gamma _g, \mathrm {U}(1))\cong \mathrm {U}(1)^{2g}$
which is identified with the Jacobian of
$\mathfrak {X}(\Gamma _g, G)=\mathrm {Hom}(\Gamma _g, \mathrm {U}(1))\cong \mathrm {U}(1)^{2g}$
which is identified with the Jacobian of
![]() $S_g$
, parametrizing topologically trivial holomorphic line bundles over a Riemannian surface diffeomorphic to
$S_g$
, parametrizing topologically trivial holomorphic line bundles over a Riemannian surface diffeomorphic to
![]() $S_g$
. The action of
$S_g$
. The action of
![]() $\mathrm {Out}(\Gamma _g)$
factors through
$\mathrm {Out}(\Gamma _g)$
factors through
![]() $\mathrm {GL}(2g,\mathbb {Z})$
acting on a product of circles, and is classically ergodic. The Dehn–Nielsen–Baer Theorem [Reference Farb and MargalitFM11] states that for such surfaces the (extended) mapping class group of isotopy classes of all homeomorphisms of
$\mathrm {GL}(2g,\mathbb {Z})$
acting on a product of circles, and is classically ergodic. The Dehn–Nielsen–Baer Theorem [Reference Farb and MargalitFM11] states that for such surfaces the (extended) mapping class group of isotopy classes of all homeomorphisms of
![]() $S_g$
is isomorphic to
$S_g$
is isomorphic to
![]() $\mathrm {Out}(\Gamma _g)$
.
$\mathrm {Out}(\Gamma _g)$
.
The above example generalizes to arbitrary compact Lie groups
![]() $K$
as follows. The smooth locus of the character variety
$K$
as follows. The smooth locus of the character variety
![]() $\mathfrak {X}(\Gamma _g,K)$
is symplectic, as proven by Goldman [Reference GoldmanGol84], and the associated invariant measure is finite, as shown by Huebschmann [Reference HuebschmannHue95]. With respect to this measure,
$\mathfrak {X}(\Gamma _g,K)$
is symplectic, as proven by Goldman [Reference GoldmanGol84], and the associated invariant measure is finite, as shown by Huebschmann [Reference HuebschmannHue95]. With respect to this measure,
![]() $\mathrm {Out}(\Gamma _g)$
acts ergodically on
$\mathrm {Out}(\Gamma _g)$
acts ergodically on
![]() $\mathfrak {X}(\Gamma _g,K)$
when
$\mathfrak {X}(\Gamma _g,K)$
when
![]() $g\geqslant 2$
, see Goldman [Reference GoldmanGol97] and Pickrell and Xia [Reference Pickrell and XiaPX02]. For non-orientable surfaces
$g\geqslant 2$
, see Goldman [Reference GoldmanGol97] and Pickrell and Xia [Reference Pickrell and XiaPX02]. For non-orientable surfaces
![]() $N$
with
$N$
with
![]() $\chi (N)\leqslant -2$
and
$\chi (N)\leqslant -2$
and
![]() $G=\mathrm {SU}(2)$
, Palesi [Reference PalesiPal11] shows ergodicity with respect to a different invariant measure.
$G=\mathrm {SU}(2)$
, Palesi [Reference PalesiPal11] shows ergodicity with respect to a different invariant measure.
The situation for non-compact Lie groups
![]() $G$
is even more complicated, and we need two definitions to describe the situation. First, for a semisimple Lie group
$G$
is even more complicated, and we need two definitions to describe the situation. First, for a semisimple Lie group
![]() $G$
with no compact factors and a rank
$G$
with no compact factors and a rank
![]() $r$
free group
$r$
free group
![]() $F_r$
, a homomorphism
$F_r$
, a homomorphism
![]() $\rho : F_r \longrightarrow G$
is said to be primitive stable if any bi-infinite geodesic in the Cayley graph of
$\rho : F_r \longrightarrow G$
is said to be primitive stable if any bi-infinite geodesic in the Cayley graph of
![]() $F_r$
defined by a primitive element (a member of free generating set) is mapped under the orbit map to a uniformly Morse quasigeodesic in the symmetric space
$F_r$
defined by a primitive element (a member of free generating set) is mapped under the orbit map to a uniformly Morse quasigeodesic in the symmetric space
![]() $G/K$
where
$G/K$
where
![]() $K$
is a maximal compact in
$K$
is a maximal compact in
![]() $G$
. Second, if
$G$
. Second, if
![]() $\rho$
is injective,
$\rho$
is injective,
![]() $\rho (F_r)$
is discrete, and
$\rho (F_r)$
is discrete, and
![]() $\rho (F_r)$
preserves and acts cocompactly on some non-empty convex subset of
$\rho (F_r)$
preserves and acts cocompactly on some non-empty convex subset of
![]() $G/K$
then
$G/K$
then
![]() $\rho$
is convex cocompact.
$\rho$
is convex cocompact.
In the case of
![]() $G=\mathrm {SL}(2,\mathbb {C})$
, Minsky [Reference MinskyMin13] showed the set
$G=\mathrm {SL}(2,\mathbb {C})$
, Minsky [Reference MinskyMin13] showed the set
![]() $\mathfrak {X}_{PS}(F_{n},G)$
of primitive stable representations is a domain of discontinuity for the action of
$\mathfrak {X}_{PS}(F_{n},G)$
of primitive stable representations is a domain of discontinuity for the action of
![]() $\mathrm {Out}(F_r)$
on
$\mathrm {Out}(F_r)$
on
![]() $\mathfrak {X}(F_{r},G)$
. Minsky also proved that
$\mathfrak {X}(F_{r},G)$
. Minsky also proved that
![]() $\mathfrak {X}_{PS}(F_{n},G)$
strictly contains the set
$\mathfrak {X}_{PS}(F_{n},G)$
strictly contains the set
![]() $\mathfrak {X}_{CC}(F_{r},G)$
of convex cocompact representations that is also a domain of discontinuity for the action of
$\mathfrak {X}_{CC}(F_{r},G)$
of convex cocompact representations that is also a domain of discontinuity for the action of
![]() $\mathrm {Out}(F_r)$
on
$\mathrm {Out}(F_r)$
on
![]() $\mathfrak {X}(F_{r},G)$
. When
$\mathfrak {X}(F_{r},G)$
. When
![]() $\Gamma = F_2$
is the fundamental group of the one
$\Gamma = F_2$
is the fundamental group of the one
![]() $1$
-holed torus
$1$
-holed torus
![]() $S_{1,1}$
, Bowditch [Reference BowditchBow98], in the case of quasi-Fuchsian representations, and more generally Tan, Wong and Zhang [Reference Tan, Wong and ZhangTWZ08], showed that there is a domain of discontinuity
$S_{1,1}$
, Bowditch [Reference BowditchBow98], in the case of quasi-Fuchsian representations, and more generally Tan, Wong and Zhang [Reference Tan, Wong and ZhangTWZ08], showed that there is a domain of discontinuity
![]() $\mathfrak {X}_{BQ}(F_{2},G)$
for the action of the mapping class group of
$\mathfrak {X}_{BQ}(F_{2},G)$
for the action of the mapping class group of
![]() $S_{1,1,}$
on the corresponding character variety
$S_{1,1,}$
on the corresponding character variety
![]() $\mathfrak {X}(F_{2},G)$
. The set
$\mathfrak {X}(F_{2},G)$
. The set
![]() $\mathfrak {X}_{BQ}(F_{2},G)$
is the set of Bowditch representations where the comparable conditions (for
$\mathfrak {X}_{BQ}(F_{2},G)$
is the set of Bowditch representations where the comparable conditions (for
![]() $G=\mathrm {SL}(2,\mathbb {C})$
) from TheoremB hold true (although [Reference BowditchBow98, Reference Tan, Wong and ZhangTWZ08] do not show
$G=\mathrm {SL}(2,\mathbb {C})$
) from TheoremB hold true (although [Reference BowditchBow98, Reference Tan, Wong and ZhangTWZ08] do not show
![]() $\mathfrak {X}_{BQ}(F_{2},G)$
strictly contains the convex cocompact representations). Later, Lee and Xu [Reference Lee and XuLX20] and Series [Reference SeriesSer19, Reference SeriesSer20] proved
$\mathfrak {X}_{BQ}(F_{2},G)$
strictly contains the convex cocompact representations). Later, Lee and Xu [Reference Lee and XuLX20] and Series [Reference SeriesSer19, Reference SeriesSer20] proved
![]() $\mathfrak {X}_{PS}(F_{2},G)=\mathfrak {X}_{BQ}(F_{2},G)$
. Schlich [Reference SchlichSch22] generalized this result to cases where
$\mathfrak {X}_{PS}(F_{2},G)=\mathfrak {X}_{BQ}(F_{2},G)$
. Schlich [Reference SchlichSch22] generalized this result to cases where
![]() $G$
is the group of isometries of a
$G$
is the group of isometries of a
![]() $\delta$
-hyperbolic space. We will discuss her results below in more detail, since they are connected with the results we present.
$\delta$
-hyperbolic space. We will discuss her results below in more detail, since they are connected with the results we present.
Following the work of Bowditch, there have been other cases where interesting domains of discontinuity have been described for relative
![]() $\mathrm {SL}(2,\mathbb {C})$
-character varieties of surface groups. For example, you can see the description of a domain of discontinuity, the Bowditch set
$\mathrm {SL}(2,\mathbb {C})$
-character varieties of surface groups. For example, you can see the description of a domain of discontinuity, the Bowditch set
![]() $\mathfrak {X}_{BQ}(\pi _1(S), G)$
, for the action of the mapping class group
$\mathfrak {X}_{BQ}(\pi _1(S), G)$
, for the action of the mapping class group
![]() $\mathrm {Mod}(S)$
on the variety
$\mathrm {Mod}(S)$
on the variety
![]() $\mathfrak {X}(\pi _1(S), G)$
, by Maloni, Palesi and Tan [Reference Maloni, Palesi and TanMPT15] when
$\mathfrak {X}(\pi _1(S), G)$
, by Maloni, Palesi and Tan [Reference Maloni, Palesi and TanMPT15] when
![]() $S$
is four
$S$
is four
![]() $4$
-holed sphere and by Maloni and Palesi [Reference Maloni and PalesiMP20] when
$4$
-holed sphere and by Maloni and Palesi [Reference Maloni and PalesiMP20] when
![]() $S$
is the three
$S$
is the three
![]() $3$
-holed projective plane. In the case when
$3$
-holed projective plane. In the case when
![]() $\Gamma$
is the fundamental group of a hyperbolic
$\Gamma$
is the fundamental group of a hyperbolic
![]() $3$
-manifold there has also been significant work finding interesting domains of discontinuity as described in this survey of Canary [Reference CanaryCan13]. When
$3$
-manifold there has also been significant work finding interesting domains of discontinuity as described in this survey of Canary [Reference CanaryCan13]. When
![]() $G$
is a semisimple group of higher rank and without compact factors, Kim and Kim [Reference Kim and KimKK20] generalized Minsky’s work on primitive-stable representations and showed that they form an open domain of discontinuity for the action of
$G$
is a semisimple group of higher rank and without compact factors, Kim and Kim [Reference Kim and KimKK20] generalized Minsky’s work on primitive-stable representations and showed that they form an open domain of discontinuity for the action of
![]() $\mathrm {Out}(\Gamma )$
on
$\mathrm {Out}(\Gamma )$
on
![]() $\mathfrak {X}(\Gamma, G)$
when
$\mathfrak {X}(\Gamma, G)$
when
![]() $\Gamma$
is a free group of rank at least
$\Gamma$
is a free group of rank at least
![]() $2$
or the fundamental group of a closed surface of genus
$2$
or the fundamental group of a closed surface of genus
![]() $g\geqslant 2$
.
$g\geqslant 2$
.
Motivated by Lubotzky [Reference LubotzkyLub11], Minsky [Reference MinskyMin13] and Gelander and Minsky [Reference Gelander and MinskyGM13] discussed primitive-stable and redundant representations in the case of free groups and
![]() $G=\mathrm {SL}(2,\mathbb {C})$
. Inspired by their work, one can imagine a decomposition of
$G=\mathrm {SL}(2,\mathbb {C})$
. Inspired by their work, one can imagine a decomposition of
![]() $\mathfrak {X}(\Gamma, G)$
into an open set where the action of
$\mathfrak {X}(\Gamma, G)$
into an open set where the action of
![]() $\mathrm {Out}(\Gamma )$
is properly discontinuous and a closed set where the action is chaotic. The only example fully understood where
$\mathrm {Out}(\Gamma )$
is properly discontinuous and a closed set where the action is chaotic. The only example fully understood where
![]() $G$
is not compact that exemplifies such a dynamical dichotomy is when
$G$
is not compact that exemplifies such a dynamical dichotomy is when
![]() $\Gamma$
is a free group of rank 2 and
$\Gamma$
is a free group of rank 2 and
![]() $G = \mathrm {SL}(2,\mathbb {R})$
, see Goldman [Reference GoldmanGol03], Goldman et al. [Reference Goldman, McShane, Stantchev and TanGMST19] and Marché and Wolff [Reference Marché and WolffMW16, Reference Marché and WolffMW19].
$G = \mathrm {SL}(2,\mathbb {R})$
, see Goldman [Reference GoldmanGol03], Goldman et al. [Reference Goldman, McShane, Stantchev and TanGMST19] and Marché and Wolff [Reference Marché and WolffMW16, Reference Marché and WolffMW19].
As summarized in Goldman [Reference GoldmanGol06], when
![]() $G$
is compact, (relative) character varieties generally exhibit non-trivial homotopy, and the action of the mapping class group exhibits non-trivial chaotic dynamics. In contrast, when
$G$
is compact, (relative) character varieties generally exhibit non-trivial homotopy, and the action of the mapping class group exhibits non-trivial chaotic dynamics. In contrast, when
![]() $G$
is non-compact, then
$G$
is non-compact, then
![]() $\mathfrak {X}(\Gamma _g,G)$
contains open sets (like the Teichmüller space or more generally Hitchin components) which are contractible and admit properly discontinuous actions. Philosophically, the action of
$\mathfrak {X}(\Gamma _g,G)$
contains open sets (like the Teichmüller space or more generally Hitchin components) which are contractible and admit properly discontinuous actions. Philosophically, the action of
![]() $\mathrm {Out}(\Gamma )$
on (relative) character varieties exhibits properties of these two extremes.
$\mathrm {Out}(\Gamma )$
on (relative) character varieties exhibits properties of these two extremes.
1.4 Relation with work of Schlich
Schlich [Reference SchlichSch22] considers representations from the fundamental group
![]() $\Gamma = \pi _1(S)$
of the one
$\Gamma = \pi _1(S)$
of the one
![]() $1$
-holed torus
$1$
-holed torus
![]() $S=S_{1,1}$
into the isometry group
$S=S_{1,1}$
into the isometry group
![]() $G$
of a geodesic and proper
$G$
of a geodesic and proper
![]() $\delta$
-hyperbolic space. Since
$\delta$
-hyperbolic space. Since
![]() ${\rm PSU}(2,1) =\mathrm {Isom}(\mathbf {H}^2_{\mathbb {C}})$
is the isometry group of the complex hyperbolic plane (see Section 2.3), her result applies to the setting we study. For the character variety
${\rm PSU}(2,1) =\mathrm {Isom}(\mathbf {H}^2_{\mathbb {C}})$
is the isometry group of the complex hyperbolic plane (see Section 2.3), her result applies to the setting we study. For the character variety
![]() $\mathfrak {X} = \mathfrak {X}(F_2,\mathrm {SU}(2,1))$
, Schlich defines two subsets of the character variety: the Bowditch set (using Definition (BQ3)) and the set of primitive-stable representations (generalizing Minsky’s definition to this setting). One of the main results of her thesis and paper shows that the two sets coincide. Since it is not hard to see that the set of primitive-stable representations is a domain of discontinuity for the action of
$\mathfrak {X} = \mathfrak {X}(F_2,\mathrm {SU}(2,1))$
, Schlich defines two subsets of the character variety: the Bowditch set (using Definition (BQ3)) and the set of primitive-stable representations (generalizing Minsky’s definition to this setting). One of the main results of her thesis and paper shows that the two sets coincide. Since it is not hard to see that the set of primitive-stable representations is a domain of discontinuity for the action of
![]() $\mathrm {Out}(F_2)$
on
$\mathrm {Out}(F_2)$
on
![]() $\mathfrak {X}$
, she also proves, as a corollary of her result, that the set of Bowditch representations also has that property. In her thesis, she also considers the case of
$\mathfrak {X}$
, she also proves, as a corollary of her result, that the set of Bowditch representations also has that property. In her thesis, she also considers the case of
![]() $S = S_{0,4}$
, a four-holed sphere, and proves that in that setting the set of ‘simple-stable’ representations coincides with the set of Bowditch’s representations [Reference SchlichSch23].
$S = S_{0,4}$
, a four-holed sphere, and proves that in that setting the set of ‘simple-stable’ representations coincides with the set of Bowditch’s representations [Reference SchlichSch23].
The main difference between our work and Schlich’s work is in the way Bowditch representations are defined. This also differentiates the challenging aspects of the work. We define our Bowditch set explicitly in terms of the character variety using the symmetry and structure understood from [Reference LawtonLaw06, Reference LawtonLaw07]. Our approach is similar to that of [Reference BowditchBow98] and its generalizations [Reference Tan, Wong and ZhangTWZ08, Reference Maloni, Palesi and TanMPT15, Reference Maloni and PalesiMP20], but adapted to representations into
![]() $\mathrm {SU}(2,1)$
where the character variety is significantly more complicated. In particular, our definition is well-adapted to computer implementations and testing since it is a definition dependent on only a finite number of conditions. Schlich’s work generalizes to isometry groups of Gromov hyperbolic spaces the results obtained for
$\mathrm {SU}(2,1)$
where the character variety is significantly more complicated. In particular, our definition is well-adapted to computer implementations and testing since it is a definition dependent on only a finite number of conditions. Schlich’s work generalizes to isometry groups of Gromov hyperbolic spaces the results obtained for
![]() $\mathrm {SL}(2,\mathbb {C})$
by Series [Reference SeriesSer19, Reference SeriesSer20]and Lee and Xu [Reference Lee and XuLX20], that for the free group
$\mathrm {SL}(2,\mathbb {C})$
by Series [Reference SeriesSer19, Reference SeriesSer20]and Lee and Xu [Reference Lee and XuLX20], that for the free group
![]() $F_2$
the notions of Bowditch representations and primitive stable representations are equal. In fact, her result gives a new independent proof of this result for
$F_2$
the notions of Bowditch representations and primitive stable representations are equal. In fact, her result gives a new independent proof of this result for
![]() $\mathrm {SL}(2,\mathbb {C})$
.
$\mathrm {SL}(2,\mathbb {C})$
.
2. Background
In this section we fix the notation which we will use in the rest of the paper and give some important definitions.
2.1 Combinatorics of simple closed curves on the one-holed torus
 $S$
$S$
Let
![]() $S= S_{1,1}$
be the one-holed torus. Its fundamental group
$S= S_{1,1}$
be the one-holed torus. Its fundamental group
![]() $\Gamma = \pi _1(S)$
is isomorphic to the non-abelian rank
$\Gamma = \pi _1(S)$
is isomorphic to the non-abelian rank
![]() $2$
free group
$2$
free group
![]() $F_2:=\langle \alpha, \beta \rangle$
. Abusing notation, we will let
$F_2:=\langle \alpha, \beta \rangle$
. Abusing notation, we will let
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
represent the (free homotopy class of) loops associated to the two generators so that the peripheral curve
$\beta$
represent the (free homotopy class of) loops associated to the two generators so that the peripheral curve
![]() $\gamma$
going around the boundary component of
$\gamma$
going around the boundary component of
![]() $S$
is oriented to be homotopic to
$S$
is oriented to be homotopic to
![]() $[\alpha, \beta ]:=\alpha \beta \alpha ^{-1}\beta ^{-1}$
.
$[\alpha, \beta ]:=\alpha \beta \alpha ^{-1}\beta ^{-1}$
.
Let
![]() $\mathcal {S}$
be the set of free homotopy classes of essential unoriented simple closed curves on
$\mathcal {S}$
be the set of free homotopy classes of essential unoriented simple closed curves on
![]() $S$
. Recall that a curve is essential if it is non-trivial and non-peripheral, or equivalently if it does not bound a disk, or a one-holed disk. We will generally omit the word essential from now on. We can identify
$S$
. Recall that a curve is essential if it is non-trivial and non-peripheral, or equivalently if it does not bound a disk, or a one-holed disk. We will generally omit the word essential from now on. We can identify
![]() $\mathcal {S}$
to a well-defined subset of
$\mathcal {S}$
to a well-defined subset of
![]() $\Gamma /\!\sim$
, where the equivalence relation
$\Gamma /\!\sim$
, where the equivalence relation
![]() $\sim$
on
$\sim$
on
![]() $\Gamma$
is defined as follows:
$\Gamma$
is defined as follows:
![]() $g \sim h$
if and only if
$g \sim h$
if and only if
![]() $g$
is conjugate to
$g$
is conjugate to
![]() $h$
or
$h$
or
![]() $h^{-1}$
.
$h^{-1}$
.
2.2 Various simplicial complexes associated to
 $S$
$S$
Definition 2.1. The curve complex
![]() $\mathcal {C}$
of the one-holed torus
$\mathcal {C}$
of the one-holed torus
![]() $S$
is defined by setting
$S$
is defined by setting
![]() $k$
-simplices to be subsets of
$k$
-simplices to be subsets of
![]() $k+1$
distinct (free homotopy classes of) essential simple closed curves in
$k+1$
distinct (free homotopy classes of) essential simple closed curves in
![]() $S$
that pairwise intersect once (up to homotopy).
$S$
that pairwise intersect once (up to homotopy).
With that definition
![]() $\mathcal {C}$
is a two-
$\mathcal {C}$
is a two-
![]() $2$
dimensional simplicial complex isomorphic to the Farey complex [Reference MinskyMin96].
$2$
dimensional simplicial complex isomorphic to the Farey complex [Reference MinskyMin96].
Definition 2.2. Let
![]() $\mathcal {T}$
be the simplicial complex defined by letting the set of
$\mathcal {T}$
be the simplicial complex defined by letting the set of
![]() $k$
-simplices in
$k$
-simplices in
![]() $\mathcal {T}$
, denoted by
$\mathcal {T}$
, denoted by
![]() $\mathcal {T}^{(k)}$
, be the set
$\mathcal {T}^{(k)}$
, be the set
![]() $\mathcal {T}^{(k)} = \mathcal {C}^{(2-k)}$
. The complex
$\mathcal {T}^{(k)} = \mathcal {C}^{(2-k)}$
. The complex
![]() $\mathcal {T}$
is called the simplicial dual of
$\mathcal {T}$
is called the simplicial dual of
![]() $\mathcal {C}$
and is a countably infinite simplicial tree properly embedded in the hyperbolic
$\mathcal {C}$
and is a countably infinite simplicial tree properly embedded in the hyperbolic
![]() $2$
-space
$2$
-space
![]() $\mathbf {H}^2$
whose vertices all have degree
$\mathbf {H}^2$
whose vertices all have degree
![]() $3$
.
$3$
.
Figure 1 illustrates
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {T}$
. Note that
$\mathcal {T}$
. Note that
![]() $\mathcal {T}$
can also be identified with the graph of ideal triangulations of
$\mathcal {T}$
can also be identified with the graph of ideal triangulations of
![]() $S$
, where edges corresponds to edge-flips. Since we will not need this identification in the rest of the paper, we will not discuss the details.
$S$
, where edges corresponds to edge-flips. Since we will not need this identification in the rest of the paper, we will not discuss the details.
The set
![]() $\Omega :=\pi _0(\mathbf {H}^2- \mathcal {T})$
is in one-to-one correspondence with the set of vertices of
$\Omega :=\pi _0(\mathbf {H}^2- \mathcal {T})$
is in one-to-one correspondence with the set of vertices of
![]() $\mathcal {C}$
and hence with the set
$\mathcal {C}$
and hence with the set
![]() $\mathcal {S}$
; that is,
$\mathcal {S}$
; that is,
Given a system of generators for
![]() $F_2$
corresponding to (free homotopy classes) of simple closed curves in
$F_2$
corresponding to (free homotopy classes) of simple closed curves in
![]() $S$
, we obtain a labeling of regions in
$S$
, we obtain a labeling of regions in
![]() $\Omega$
. For example, with
$\Omega$
. For example, with
![]() $F_2 = \langle \alpha, \beta \rangle$
we obtain the labeling in Figure 1. As you can see, the labeling is defined from the starting central edge
$F_2 = \langle \alpha, \beta \rangle$
we obtain the labeling in Figure 1. As you can see, the labeling is defined from the starting central edge
![]() $e = \{\alpha, \beta \}$
corresponding to the intersection of the regions in
$e = \{\alpha, \beta \}$
corresponding to the intersection of the regions in
![]() $\Omega$
labeled
$\Omega$
labeled
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
, and is defined, for a certain region
$\beta$
, and is defined, for a certain region
![]() $X$
, as the product of the two regions adjacent to
$X$
, as the product of the two regions adjacent to
![]() $X$
but closer to the initial edge
$X$
but closer to the initial edge
![]() $e$
. Note that when doing this product the region
$e$
. Note that when doing this product the region
![]() $\beta$
needs to be considered as
$\beta$
needs to be considered as
![]() $\beta$
on the ‘left-hand side’ of the edge
$\beta$
on the ‘left-hand side’ of the edge
![]() $e$
and
$e$
and
![]() $\beta ^{-1}$
on the ‘right-hand side’ of the edge
$\beta ^{-1}$
on the ‘right-hand side’ of the edge
![]() $e$
.
$e$
.
Definition 2.3. The edge graph
![]() $\mathcal {E}$
is the graph whose vertices correspond to edges of
$\mathcal {E}$
is the graph whose vertices correspond to edges of
![]() $\mathcal {T}$
, and whose edges correspond to adjacency. More precisely, if we denote by
$\mathcal {T}$
, and whose edges correspond to adjacency. More precisely, if we denote by
![]() $\mathcal {E}^{(k)}$
the set of
$\mathcal {E}^{(k)}$
the set of
![]() $k$
-simplices, we have that
$k$
-simplices, we have that
![]() $\mathcal {E}^{(0)} = \mathcal {T}^{(1)} = \mathcal {C}^{(1)}$
and the edges of
$\mathcal {E}^{(0)} = \mathcal {T}^{(1)} = \mathcal {C}^{(1)}$
and the edges of
![]() $\mathcal {E}$
correspond to edges that are the boundary of the same triangle in
$\mathcal {E}$
correspond to edges that are the boundary of the same triangle in
![]() $\mathcal {C}^{(2)}$
.
$\mathcal {C}^{(2)}$
.
Note that
![]() $\mathcal {E}$
is quasi-isometric to
$\mathcal {E}$
is quasi-isometric to
![]() $\mathcal {T}$
. In fact, one can see that
$\mathcal {T}$
. In fact, one can see that
![]() $\mathcal {E}$
is a ‘trivalent tree of triangles’ in the sense that it is a graph made of triangles (one for each triangle
$\mathcal {E}$
is a ‘trivalent tree of triangles’ in the sense that it is a graph made of triangles (one for each triangle
![]() $T$
in
$T$
in
![]() $\mathcal {C}^{(2)}$
or, equivalently, one for each vertex of
$\mathcal {C}^{(2)}$
or, equivalently, one for each vertex of
![]() $\mathcal T$
).
$\mathcal T$
).
Since each edge of
![]() $\mathcal {T}$
is uniquely determined by two (free homotopy classes of) simple closed curves intersecting once, we will denote vertices of
$\mathcal {T}$
is uniquely determined by two (free homotopy classes of) simple closed curves intersecting once, we will denote vertices of
![]() $\mathcal E$
as
$\mathcal E$
as
![]() $v = (\alpha, \beta ) \in \mathcal {E}^{(0)}$
. It will be convenient for some proofs to denote such a vertex
$v = (\alpha, \beta ) \in \mathcal {E}^{(0)}$
. It will be convenient for some proofs to denote such a vertex
![]() $v$
as
$v$
as
![]() $(\alpha, \beta ;\gamma, \delta )$
, where
$(\alpha, \beta ;\gamma, \delta )$
, where
![]() $\gamma, \delta$
are regions adjacent to
$\gamma, \delta$
are regions adjacent to
![]() $(\alpha, \beta )$
considered as an element in
$(\alpha, \beta )$
considered as an element in
![]() $\mathcal {T}^{(1)}$
. Each edge of
$\mathcal {T}^{(1)}$
. Each edge of
![]() $\mathcal E$
is uniquely determined by the choice of a triangle
$\mathcal E$
is uniquely determined by the choice of a triangle
![]() $T$
in
$T$
in
![]() $\mathcal {C}^{(2)}$
plus the choice of one of its vertices, so we will denote edges of
$\mathcal {C}^{(2)}$
plus the choice of one of its vertices, so we will denote edges of
![]() $\mathcal E$
as
$\mathcal E$
as
![]() $e = (\alpha ; \beta, \gamma ) \in \mathcal {E}^{(1)}$
. We will also have to denote oriented edges, so in that case we will use the notation
$e = (\alpha ; \beta, \gamma ) \in \mathcal {E}^{(1)}$
. We will also have to denote oriented edges, so in that case we will use the notation
![]() $(\alpha, \beta, \gamma ; \delta, \delta ')$
. See Figure 2.
$(\alpha, \beta, \gamma ; \delta, \delta ')$
. See Figure 2.
Additionally, we will have to color the edges of
![]() $\mathcal {E}$
with four colors so that the edges of each triangle have the same color and each triangle is adjacent to triangles with distinct coloring. This coloring can be extended to color the vertices of
$\mathcal {E}$
with four colors so that the edges of each triangle have the same color and each triangle is adjacent to triangles with distinct coloring. This coloring can be extended to color the vertices of
![]() $\mathcal {C}$
(or equivalently to the connected components of
$\mathcal {C}$
(or equivalently to the connected components of
![]() $\mathbf {H}^2 \setminus \mathcal {T}$
). This is possible since each such region is bounded by triangles colored with three distinct colors. Therefore, the region will be colored in the color that does not appear in the triangles going around the region. See Figure 3.
$\mathbf {H}^2 \setminus \mathcal {T}$
). This is possible since each such region is bounded by triangles colored with three distinct colors. Therefore, the region will be colored in the color that does not appear in the triangles going around the region. See Figure 3.

Figure 3. The complex
![]() $\mathcal {E}$
with the coloring of its edges and regions of
$\mathcal {E}$
with the coloring of its edges and regions of
![]() $\mathbf {H}^2 \setminus \mathcal {T}$
.
$\mathbf {H}^2 \setminus \mathcal {T}$
.
2.3 Complex hyperbolic geometry
 $\mathbf {H}^2_{\mathbb {C}}$
$\mathbf {H}^2_{\mathbb {C}}$
Let
![]() $\mathbb {C}^{n,1}\cong \mathbb {C}^n\times \mathbb {C}$
be the
$\mathbb {C}^{n,1}\cong \mathbb {C}^n\times \mathbb {C}$
be the
![]() $(n+1)$
-dimensional complex vector space with Hermitian pairing defined for vectors
$(n+1)$
-dimensional complex vector space with Hermitian pairing defined for vectors
![]() $(\mathbf {x},x_{n+1})\in \mathbb {C}^{n+1}$
by
$(\mathbf {x},x_{n+1})\in \mathbb {C}^{n+1}$
by
 \begin{equation*}\langle (\mathbf {x},x_{n+1}),(\mathbf {y},y_{n+1})\rangle :=\left (\sum _{i=1}^{n}x_i\overline {y_i}\right )-x_{n+1}\overline {y_{n+1}}.\end{equation*}
\begin{equation*}\langle (\mathbf {x},x_{n+1}),(\mathbf {y},y_{n+1})\rangle :=\left (\sum _{i=1}^{n}x_i\overline {y_i}\right )-x_{n+1}\overline {y_{n+1}}.\end{equation*}
We say a vector
![]() $\mathbf {v}$
is negative if and only if
$\mathbf {v}$
is negative if and only if
![]() $\langle \mathbf {v},\mathbf {v}\rangle \lt 0$
. Let
$\langle \mathbf {v},\mathbf {v}\rangle \lt 0$
. Let
![]() $\mathbf {P}(\mathbb {C}^{n,1}):=(\mathbb {C}^{n,1}-\{\mathbf {0}\})/\mathbb {C}^*$
be the space of lines in
$\mathbf {P}(\mathbb {C}^{n,1}):=(\mathbb {C}^{n,1}-\{\mathbf {0}\})/\mathbb {C}^*$
be the space of lines in
![]() $\mathbb {C}^{n,1}$
through the origin. Then the complex hyperbolic space of dimension
$\mathbb {C}^{n,1}$
through the origin. Then the complex hyperbolic space of dimension
![]() $n$
is defined to be
$n$
is defined to be
![]() $\mathbf {H}_{\mathbb {C}}^n:=\{[\mathbf {v}]\in \mathbf {P}(\mathbb {C}^{n,1})\ |\ \langle \mathbf {v},\mathbf {v}\rangle \lt 0\}$
.
$\mathbf {H}_{\mathbb {C}}^n:=\{[\mathbf {v}]\in \mathbf {P}(\mathbb {C}^{n,1})\ |\ \langle \mathbf {v},\mathbf {v}\rangle \lt 0\}$
.
There is a natural copy of
![]() $\mathbb {C}^n$
in
$\mathbb {C}^n$
in
![]() $\mathbf {P}(\mathbb {C}^{n,1})$
given by
$\mathbf {P}(\mathbb {C}^{n,1})$
given by
The biholomorphism
![]() $\varphi :\mathbb {C}^n\longrightarrow \mathbb {A}$
is given by
$\varphi :\mathbb {C}^n\longrightarrow \mathbb {A}$
is given by
![]() $\varphi (\mathbf {v})=[(\mathbf {v},1)]$
. We observe that
$\varphi (\mathbf {v})=[(\mathbf {v},1)]$
. We observe that
![]() $\mathbf {H}_{\mathbb {C}}^n\subset \mathbb {A}$
since if
$\mathbf {H}_{\mathbb {C}}^n\subset \mathbb {A}$
since if
![]() $v_{n+1}=0$
then
$v_{n+1}=0$
then
![]() $\langle \mathbf {v},\mathbf {v}\rangle \gt 0$
. Then restricting
$\langle \mathbf {v},\mathbf {v}\rangle \gt 0$
. Then restricting
![]() $\varphi ^{-1}$
to
$\varphi ^{-1}$
to
![]() $\mathbf {H}_{\mathbb {C}}^n$
we see that
$\mathbf {H}_{\mathbb {C}}^n$
we see that
![]() $\mathbf {H}_{\mathbb {C}}^n$
is biholomorphic to the unit ball in
$\mathbf {H}_{\mathbb {C}}^n$
is biholomorphic to the unit ball in
![]() $\mathbb {C}^n$
since
$\mathbb {C}^n$
since
![]() $\langle (\mathbf {v},1),(\mathbf {v},1)\rangle \lt 0$
if and only if
$\langle (\mathbf {v},1),(\mathbf {v},1)\rangle \lt 0$
if and only if
![]() $\sum _{i=1}^{n}v_i\overline {v_i}\lt 1$
.
$\sum _{i=1}^{n}v_i\overline {v_i}\lt 1$
.
Consequently, the boundary of
![]() $\mathbf {H}_{\mathbb {C}}^n$
is homeomorphic to the unit sphere in
$\mathbf {H}_{\mathbb {C}}^n$
is homeomorphic to the unit sphere in
![]() $\mathbb {C}^n$
:
$\mathbb {C}^n$
:
We let
![]() $\mathrm {U}(n,1)$
be the subgroup of
$\mathrm {U}(n,1)$
be the subgroup of
![]() $\mathrm {GL}(n+1,\mathbb {C})$
consisting of matrices
$\mathrm {GL}(n+1,\mathbb {C})$
consisting of matrices
![]() $A$
such that
$A$
such that
The image of
![]() $\mathrm {U}(n,1)$
in
$\mathrm {U}(n,1)$
in
![]() $\mathrm {PGL}(n+1,\mathbb {C})$
, denoted by
$\mathrm {PGL}(n+1,\mathbb {C})$
, denoted by
![]() $\mathrm {PU}(n,1)$
, is the group of biholomorphisms of
$\mathrm {PU}(n,1)$
, is the group of biholomorphisms of
![]() $\mathbf {H}_{\mathbb {C}}^n$
(see [Reference GoldmanGol99]).
$\mathbf {H}_{\mathbb {C}}^n$
(see [Reference GoldmanGol99]).
Here
![]() $\mathrm {PU}(n,1)$
acts transitively on
$\mathrm {PU}(n,1)$
acts transitively on
![]() $\mathbf {H}_{\mathbb {C}}^n$
with stabilizer isomorphic to
$\mathbf {H}_{\mathbb {C}}^n$
with stabilizer isomorphic to
![]() $\mathrm {U}(n)$
. Thus, we see that the complex hyperbolic space is a homogeneous space
$\mathrm {U}(n)$
. Thus, we see that the complex hyperbolic space is a homogeneous space
2.4
 $\mathrm {SL}(3,\mathbb {C})$
and
$\mathrm {SL}(3,\mathbb {C})$
and
 $\mathrm {SU}(2,1)$
$\mathrm {SU}(2,1)$
Let
![]() $\mathrm {SL}(3,\mathbb {C})$
be the Lie group of
$\mathrm {SL}(3,\mathbb {C})$
be the Lie group of
![]() $3\times 3$
complex matrices of unit determinant, which is also a complex affine variety since it is the zero locus of the determinant polynomial minus
$3\times 3$
complex matrices of unit determinant, which is also a complex affine variety since it is the zero locus of the determinant polynomial minus
![]() $1$
.
$1$
.
We review a few facts about two real forms of
![]() $\mathrm {SL}(3,\mathbb {C})$
. First,
$\mathrm {SL}(3,\mathbb {C})$
. First,
where
![]() $\dagger$
means ‘transpose’. Letting
$\dagger$
means ‘transpose’. Letting
 \begin{equation*}J=\left (\begin{array}{c@{\quad}c@{\quad}c}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & -1\end{array}\right ),\end{equation*}
\begin{equation*}J=\left (\begin{array}{c@{\quad}c@{\quad}c}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & -1\end{array}\right ),\end{equation*}
we secondly have
Consequently,
![]() $\mathrm {tr}(A^{-1})=\overline {\mathrm {tr}(A)}$
for any
$\mathrm {tr}(A^{-1})=\overline {\mathrm {tr}(A)}$
for any
![]() $A\in \mathrm {SU}(3)\cup \mathrm {SU}(2,1)$
.
$A\in \mathrm {SU}(3)\cup \mathrm {SU}(2,1)$
.
The following lemma is well-known (see, for example, [Reference GoldmanGol99, Exercise 3.1.1]), but we include a proof since it is an essential fact in our proof of TheoremC.
Lemma 2.4.
Any maximal compact subgroup of
![]() $\mathrm {SU}(2,1)$
is isomorphic to
$\mathrm {SU}(2,1)$
is isomorphic to
![]() $\mathrm {U}(2)$
. In addition, the center of
$\mathrm {U}(2)$
. In addition, the center of
![]() $\mathrm {SU}(2,1)$
is isomorphic to
$\mathrm {SU}(2,1)$
is isomorphic to
![]() $\mathbb {Z}_3$
.
$\mathbb {Z}_3$
.
Proof.
In general, the group
![]() $\mathrm {U}(p)\times \mathrm {U}(q)$
is a maximal compact in
$\mathrm {U}(p)\times \mathrm {U}(q)$
is a maximal compact in
![]() $\mathrm {U}(p,q)$
and so
$\mathrm {U}(p,q)$
and so
![]() $\mathrm {S}(\mathrm {U}(p)\times \mathrm {U}(q))$
is a maximal compact in
$\mathrm {S}(\mathrm {U}(p)\times \mathrm {U}(q))$
is a maximal compact in
![]() $\mathrm {SU}(p,q)$
. In the case of
$\mathrm {SU}(p,q)$
. In the case of
![]() $\mathrm {SU}(2,1)$
we have that
$\mathrm {SU}(2,1)$
we have that
![]() $\mathrm {S}(\mathrm {U}(2)\times \mathrm {U}(1))=\{(A,\lambda )\in \mathrm {U}(2)\times \mathrm {U}(1)\ |\ \mathrm {Det}(A)\lambda=1\}$
. On the other hand, this group is isomorphic to
$\mathrm {S}(\mathrm {U}(2)\times \mathrm {U}(1))=\{(A,\lambda )\in \mathrm {U}(2)\times \mathrm {U}(1)\ |\ \mathrm {Det}(A)\lambda=1\}$
. On the other hand, this group is isomorphic to
![]() $\mathrm {U}(2)$
simply by sending
$\mathrm {U}(2)$
simply by sending
![]() $(A,\lambda )\mapsto A$
. Since all maximal compact subgroups are isomorphic, the first result follows.
$(A,\lambda )\mapsto A$
. Since all maximal compact subgroups are isomorphic, the first result follows.
Now we compute the center. Suppose
![]() $Z\in \mathrm {SU}(2,1)$
is in the center
$Z\in \mathrm {SU}(2,1)$
is in the center
![]() $Z(\mathrm {SU}(2,1))\leqslant \mathrm {SU}(2,1)$
. Then for all
$Z(\mathrm {SU}(2,1))\leqslant \mathrm {SU}(2,1)$
. Then for all
![]() $A\in \mathrm {SU}(2,1)$
we have
$A\in \mathrm {SU}(2,1)$
we have
![]() $AZ=ZA$
. On the other hand, this equation, which is necessarily algebraic, holds on the Zariski closure of
$AZ=ZA$
. On the other hand, this equation, which is necessarily algebraic, holds on the Zariski closure of
![]() $\mathrm {SU}(2,1)$
, which is
$\mathrm {SU}(2,1)$
, which is
![]() $\mathrm {SL}(3,\mathbb {C})$
. So
$\mathrm {SL}(3,\mathbb {C})$
. So
![]() $Z$
is a central matrix in
$Z$
is a central matrix in
![]() $\mathrm {SL}(3,\mathbb {C})$
and so a scalar multiple of the identity. The only such matrices are
$\mathrm {SL}(3,\mathbb {C})$
and so a scalar multiple of the identity. The only such matrices are
![]() $\{\omega I, \omega^2 I, I\}\cong \mathbb {Z}_3$
, where
$\{\omega I, \omega^2 I, I\}\cong \mathbb {Z}_3$
, where
![]() $\omega$
is a primitive cube root of unity.
$\omega$
is a primitive cube root of unity.
An automorphism of the complex hyperbolic space
![]() $\mathbf {H}^2_{\mathbb {C}}\subset \mathbb {P}(\mathbb {C}^{2,1})$
, represented by an element in
$\mathbf {H}^2_{\mathbb {C}}\subset \mathbb {P}(\mathbb {C}^{2,1})$
, represented by an element in
![]() $ \mathrm {PSU}(2,1):=\mathrm {SU}(2,1)/Z(\mathrm {SU}(2,1))$
, lifts to an element of
$ \mathrm {PSU}(2,1):=\mathrm {SU}(2,1)/Z(\mathrm {SU}(2,1))$
, lifts to an element of
![]() $\mathrm {SU}(2,1)$
, and the fixed points in
$\mathrm {SU}(2,1)$
, and the fixed points in
![]() $\mathbf {H}^2_{\mathbb {C}}\cup \partial \mathbf {H}^2_{\mathbb {C}}$
correspond to eigenvectors of this lift. For each such automorphism, there are three lifts corresponding to the cubic roots of unity
$\mathbf {H}^2_{\mathbb {C}}\cup \partial \mathbf {H}^2_{\mathbb {C}}$
correspond to eigenvectors of this lift. For each such automorphism, there are three lifts corresponding to the cubic roots of unity
![]() $\zeta _3\subset S^1\subset \mathbb {C}$
. The following definition is taken from [Reference GoldmanGol99, Section 6.2.1].
$\zeta _3\subset S^1\subset \mathbb {C}$
. The following definition is taken from [Reference GoldmanGol99, Section 6.2.1].
Definition 2.5. An element in
![]() $\mathrm {SU}(2,1)$
is called:
$\mathrm {SU}(2,1)$
is called:
-
(i) elliptic if it has a fixed point in
 $\mathbf {H}^2_{\mathbb {C}}$
;
$\mathbf {H}^2_{\mathbb {C}}$
; -
(ii) parabolic if it has a unique fixed point on
 $\partial \mathbf {H}^2_{\mathbb {C}}$
;
$\partial \mathbf {H}^2_{\mathbb {C}}$
; -
(iii) unipotent if it is parabolic and all the eigenvalues are equal;
-
(iv) loxodromic if it fixes a unique pair of points on
 $\partial \mathbf {H}^2_{\mathbb {C}}$
.
$\partial \mathbf {H}^2_{\mathbb {C}}$
.
Given a matrix
![]() $A\in \textrm {SU} (2,1)$
such that
$A\in \textrm {SU} (2,1)$
such that
![]() $t = \mathrm {tr}(A)$
, its characteristic polynomial, whose zeros are the eigenvalues of
$t = \mathrm {tr}(A)$
, its characteristic polynomial, whose zeros are the eigenvalues of
![]() $A$
, is the polynomial
$A$
, is the polynomial
![]() $\chi _A(x) = x^3 - t x^2 + \overline t x -1$
. The resultant of
$\chi _A(x) = x^3 - t x^2 + \overline t x -1$
. The resultant of
![]() $\chi _A$
and its derivative tells us when
$\chi _A$
and its derivative tells us when
![]() $\chi _A$
has multiple roots, and hence when
$\chi _A$
has multiple roots, and hence when
![]() $A$
has an eigenvalue with multiplicity greater than
$A$
has an eigenvalue with multiplicity greater than
![]() $1$
. Let
$1$
. Let
![]() $f\colon \thinspace \mathbb {C} \longrightarrow \mathbb {R}$
be defined by
$f\colon \thinspace \mathbb {C} \longrightarrow \mathbb {R}$
be defined by
This function vanishes on a deltoid centered at
![]() $0$
of radius
$0$
of radius
![]() $3$
, see Figure 4.
$3$
, see Figure 4.

Figure 4.
![]() $f(t)=0$
.
$f(t)=0$
.
Theorem 2.6 (Theorem 6.2.4, [Reference GoldmanGol99]). The map
![]() $\mathrm {tr}\colon \thinspace \mathrm {SU}(2,1)\longrightarrow \mathbb {C}$
is surjective. If
$\mathrm {tr}\colon \thinspace \mathrm {SU}(2,1)\longrightarrow \mathbb {C}$
is surjective. If
![]() $A,B\in \mathrm {SU}(2,1)$
are loxodromic and
$A,B\in \mathrm {SU}(2,1)$
are loxodromic and
![]() $\mathrm {tr}(A)=\mathrm {tr}(B)$
, then
$\mathrm {tr}(A)=\mathrm {tr}(B)$
, then
![]() $A$
and
$A$
and
![]() $B$
are conjugate.
$B$
are conjugate.
In addition, for any
![]() $A\in \mathrm {SU}(2,1)$
with
$A\in \mathrm {SU}(2,1)$
with
![]() $t = \mathrm {tr}(A)$
we have:
$t = \mathrm {tr}(A)$
we have:
-
(i)
 $A$
is elliptic with distinct eigenvalues if and only if
$A$
is elliptic with distinct eigenvalues if and only if
 $f(t)\lt 0$
;
$f(t)\lt 0$
; -
(ii)
 $A$
is loxodromic if and only if
$A$
is loxodromic if and only if
 $f(t)\gt 0$
;
$f(t)\gt 0$
; -
(iii)
 $A$
is parabolic but not unipotent if and only if
$A$
is parabolic but not unipotent if and only if
 $A$
is not elliptic and
$A$
is not elliptic and
 $t\in f^{-1}(0)-3\zeta _3$
;
$t\in f^{-1}(0)-3\zeta _3$
; -
(iv)
 $A$
is a complex-reflection if and only if
$A$
is a complex-reflection if and only if
 $A$
is elliptic and
$A$
is elliptic and
 $t\in f^{-1}(0)-3\zeta _3$
;
$t\in f^{-1}(0)-3\zeta _3$
; -
(v)
 $A$
is an unipotent automorphism of
$A$
is an unipotent automorphism of
 $\mathbf {H}^2_{\mathbb {C}}$
or the identity map if and only if
$\mathbf {H}^2_{\mathbb {C}}$
or the identity map if and only if
 $t\in 3\zeta _3$
.
$t\in 3\zeta _3$
.
The following result is a corollary to the above theorem.
Corollary 2.7 ([Reference GoldmanGol99]). Let
![]() $A\in \mathrm {SU}(2,1)$
with eigenvalues
$A\in \mathrm {SU}(2,1)$
with eigenvalues
![]() $\lambda _1,\lambda _2,\lambda _3$
, and let
$\lambda _1,\lambda _2,\lambda _3$
, and let
![]() $t = \mathrm {tr}(A)$
. We have the following.
$t = \mathrm {tr}(A)$
. We have the following.
-
(i) If
 $f(t) \gt 0$
, then
$f(t) \gt 0$
, then
 $A$
is loxodromic, and its eigenvalues are all distinct: one is inside, one is outside and one is on the unit circle.
$A$
is loxodromic, and its eigenvalues are all distinct: one is inside, one is outside and one is on the unit circle.
-
(ii) If
 $f(t)=0$
, then
$f(t)=0$
, then
 $A$
has an eigenvalue of multiplicity at least
$A$
has an eigenvalue of multiplicity at least
 $2$
, and all eigenvalues are on the unit circle.
$2$
, and all eigenvalues are on the unit circle.
-
(iii) If
 $f(t) \lt 0$
, then
$f(t) \lt 0$
, then
 $A$
is regular elliptic, and has three distinct eigenvalue s satisfying
$A$
is regular elliptic, and has three distinct eigenvalue s satisfying
 $|\lambda _i | = 1$
.
$|\lambda _i | = 1$
.
2.4.1
 $\mathrm {SL}(3,\mathbb {C})$
-character variety
$\mathrm {SL}(3,\mathbb {C})$
-character variety
Let
![]() $S_{1,1}$
be the one-holed torus. The fundamental group of
$S_{1,1}$
be the one-holed torus. The fundamental group of
![]() $S_{1,1}$
is isomorphic to a rank
$S_{1,1}$
is isomorphic to a rank
![]() $2$
free group
$2$
free group
where
![]() $\gamma$
corresponds to a loop around the boundary circle and
$\gamma$
corresponds to a loop around the boundary circle and
![]() $\alpha, \beta$
are loops of longitude and latitude in the torus, as we discussed in Section 2.2.
$\alpha, \beta$
are loops of longitude and latitude in the torus, as we discussed in Section 2.2.
The set of group homomorphisms
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is in bijective correspondence with
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is in bijective correspondence with
![]() $\mathrm {SL}(3,\mathbb {C})\times \mathrm {SL}(3,\mathbb {C})$
by sending a homomorphism
$\mathrm {SL}(3,\mathbb {C})\times \mathrm {SL}(3,\mathbb {C})$
by sending a homomorphism
![]() $\rho$
to
$\rho$
to
![]() $(\rho (\alpha ),\rho (\beta ))$
. Since products of smooth manifolds are smooth manifolds and products of affine varieties are affine varieties, we can give the structure of a complex affine algebraic variety (and a smooth manifold) to
$(\rho (\alpha ),\rho (\beta ))$
. Since products of smooth manifolds are smooth manifolds and products of affine varieties are affine varieties, we can give the structure of a complex affine algebraic variety (and a smooth manifold) to
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
.
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
.
The group
![]() $\mathrm {SL}(3,\mathbb {C})$
acts on
$\mathrm {SL}(3,\mathbb {C})$
acts on
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
by conjugation, which becomes simultaneous conjugation under the identification with
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
by conjugation, which becomes simultaneous conjugation under the identification with
![]() $\mathrm {SL}(3,\mathbb {C})\times \mathrm {SL}(3,\mathbb {C})$
. Precisely, for
$\mathrm {SL}(3,\mathbb {C})\times \mathrm {SL}(3,\mathbb {C})$
. Precisely, for
![]() $g \in \mathrm {SL}(3,\mathbb {C})$
and
$g \in \mathrm {SL}(3,\mathbb {C})$
and
![]() $\rho \in \mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
the action is defined by
$\rho \in \mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
the action is defined by
![]() $g\cdot \rho =g\rho g^{-1}$
, and for
$g\cdot \rho =g\rho g^{-1}$
, and for
![]() $(A,B)\in \mathrm {SL}(3,\mathbb {C})\times \mathrm {SL}(3,\mathbb {C})$
we have
$(A,B)\in \mathrm {SL}(3,\mathbb {C})\times \mathrm {SL}(3,\mathbb {C})$
we have
![]() $g\cdot (A,B)=(gAg^{-1}, gBg^{-1})$
.
$g\cdot (A,B)=(gAg^{-1}, gBg^{-1})$
.
We are interested in the moduli space of such homomorphisms up to the equivalence defined by this action. The quotient
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))/\mathrm {SL}(3,\mathbb {C})$
does not satisfy the
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))/\mathrm {SL}(3,\mathbb {C})$
does not satisfy the
![]() $T_1$
-separation axiom since some points are not closed (corresponding to non-closed orbits in
$T_1$
-separation axiom since some points are not closed (corresponding to non-closed orbits in
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
). There is a natural way to make it satisfy the
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
). There is a natural way to make it satisfy the
![]() $T_1$
-separation axiom: remove the orbits that are not closed in
$T_1$
-separation axiom: remove the orbits that are not closed in
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
. Let
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
. Let
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))^*$
be the subspace of
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))^*$
be the subspace of
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
that consists of homomorphisms with closed conjugation orbits. Then the polystable quotient
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
that consists of homomorphisms with closed conjugation orbits. Then the polystable quotient
satisfies the
![]() $T_1$
-separation axiom.
$T_1$
-separation axiom.
However, one can show that it is homeomorphic to the Geometric Invariant Theory (GIT) quotient
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))/\!\!/\mathrm {SL}(3,\mathbb {C})$
, where the latter is given the induced metric topology from being an affine variety (called the analytic or strong topology). See Florentino and Lawton [Reference Florentino and LawtonFL14, Theorem 2.1] for a proof. Thus,
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))/\!\!/\mathrm {SL}(3,\mathbb {C})$
, where the latter is given the induced metric topology from being an affine variety (called the analytic or strong topology). See Florentino and Lawton [Reference Florentino and LawtonFL14, Theorem 2.1] for a proof. Thus,
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
has the structure of a stratified manifold (and so is a metric space). Moreover,
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
has the structure of a stratified manifold (and so is a metric space). Moreover,
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is homotopic to the non-Hausdorff space
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is homotopic to the non-Hausdorff space
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))/\mathrm {SL}(3,\mathbb {C})$
just the same (see Florentino, Lawton and Ramras [Reference Florentino, Lawton and RamrasFLR17, Proposition 3.4]).
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))/\mathrm {SL}(3,\mathbb {C})$
just the same (see Florentino, Lawton and Ramras [Reference Florentino, Lawton and RamrasFLR17, Proposition 3.4]).
To understand the affine variety structure on
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
, which approximates the non-Hausdorff space
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
, which approximates the non-Hausdorff space
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))/\mathrm {SL}(3,\mathbb {C})$
, we need to understand the ring of polynomial functions on it.
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))/\mathrm {SL}(3,\mathbb {C})$
, we need to understand the ring of polynomial functions on it.
Let
![]() $\mathbf {X}=(x_{ij})_{1\leqslant i,j\leqslant 3}$
and
$\mathbf {X}=(x_{ij})_{1\leqslant i,j\leqslant 3}$
and
![]() $\mathbf {Y}=(y_{ij})_{1\leqslant i,j\leqslant 3}$
be two
$\mathbf {Y}=(y_{ij})_{1\leqslant i,j\leqslant 3}$
be two
![]() $3\times 3$
matrices of variables (called ‘generic matrices’). Then the ring of polynomials on
$3\times 3$
matrices of variables (called ‘generic matrices’). Then the ring of polynomials on
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is
Since
![]() $\mathrm {SL}(3,\mathbb {C})$
acts algebraically by conjugation on
$\mathrm {SL}(3,\mathbb {C})$
acts algebraically by conjugation on
![]() $\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
, there is an action on
$\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))$
, there is an action on
![]() $\mathbb {C}[\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))]$
given by
$\mathbb {C}[\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))]$
given by
![]() $(g\cdot f)(\rho )=f(g^{-1}\rho g)$
for
$(g\cdot f)(\rho )=f(g^{-1}\rho g)$
for
![]() $g\in \mathrm {SL}(3,\mathbb {C})$
. The ring of polynomials on
$g\in \mathrm {SL}(3,\mathbb {C})$
. The ring of polynomials on
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is then
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is then
 \begin{align*} \mathbb {C}[\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))] & :=\mathbb {C}[\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))]^{\mathrm {SL}(3,\mathbb {C})}\\ & := \{f\in \mathbb {C}[\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))]\ |\ g\cdot f=f\text { for all } g\in \mathrm {SL}(3,\mathbb {C})\}. \end{align*}
\begin{align*} \mathbb {C}[\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))] & :=\mathbb {C}[\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))]^{\mathrm {SL}(3,\mathbb {C})}\\ & := \{f\in \mathbb {C}[\mathrm {Hom}(F_2,\mathrm {SL}(3,\mathbb {C}))]\ |\ g\cdot f=f\text { for all } g\in \mathrm {SL}(3,\mathbb {C})\}. \end{align*}
One of the main theorems in Lawton [Reference LawtonLaw06, Reference LawtonLaw07] states that
where
![]() $P,Q\in \mathbb {C}[x,y,z,t,A,B,C,D]$
and the polynomial
$P,Q\in \mathbb {C}[x,y,z,t,A,B,C,D]$
and the polynomial
![]() $s^2-Ps+Q$
is irreducible.
$s^2-Ps+Q$
is irreducible.
Consequently, we have the following.
Theorem 2.8 ([Reference LawtonLaw06, Reference LawtonLaw07]).
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is a hypersurface in
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is a hypersurface in
![]() $\mathbb {C}^9$
that is a branched double cover of
$\mathbb {C}^9$
that is a branched double cover of
![]() $\mathbb {C}^8$
. The branching locus is exactly the representations that are fixed by transpose.
$\mathbb {C}^8$
. The branching locus is exactly the representations that are fixed by transpose.
The explicit forms of
![]() $P$
and
$P$
and
![]() $Q$
are
$Q$
are
and
![]() $Q=9 + t^3 - 6 t D+D^3 + x^3 - 6 x A+t D x A+A^3 + t x^2 y+3 t A y - 2 D^2 A y - t x A^2 y+D x y^2 + $
$Q=9 + t^3 - 6 t D+D^3 + x^3 - 6 x A+t D x A+A^3 + t x^2 y+3 t A y - 2 D^2 A y - t x A^2 y+D x y^2 + $
![]() $ D A^2 y^2\; +\; y^3\; -\; x A y^3\; -\; 2 t^2 x B\;+\; 3 D x B\; -\; D x^2 A B+D A^2 B - 6 y B+t D y B - x^3 y B+x A y B+$
$ D A^2 y^2\; +\; y^3\; -\; x A y^3\; -\; 2 t^2 x B\;+\; 3 D x B\; -\; D x^2 A B+D A^2 B - 6 y B+t D y B - x^3 y B+x A y B+$
![]() $ x^2 A^2 y B - A^3 y B - t A y^2 B+t x^2 B^2 + t A B^2 - D x y B^2 + x A y^2 B^2 + B^3 - x A B^3\; -\; 3 t x z+D^2 x z\,+ $
$ x^2 A^2 y B - A^3 y B - t A y^2 B+t x^2 B^2 + t A B^2 - D x y B^2 + x A y^2 B^2 + B^3 - x A B^3\; -\; 3 t x z+D^2 x z\,+ $
![]() $ t A^2 z+t^2 y z -3 D y z - D x A y z\; +\; x^2 y^2 z\; +\; A y^2 z\; +\; x^2 B z\; +\; 3 A B z\; - x A^2 B z - t x y B z+D B^2 z - $
$ t A^2 z+t^2 y z -3 D y z - D x A y z\; +\; x^2 y^2 z\; +\; A y^2 z\; +\; x^2 B z\; +\; 3 A B z\; - x A^2 B z - t x y B z+D B^2 z - $
![]() $ A y B^2 z+D A z^2\; -\; 2 x y z^2\; +\; t B z^2\; +\; z^3\; +\; D x^2 C\; +\; t^2 A C - 3 D A C\; +\; 3 x y C - x^2 A y C + A^2 y C + $
$ A y B^2 z+D A z^2\; -\; 2 x y z^2\; +\; t B z^2\; +\; z^3\; +\; D x^2 C\; +\; t^2 A C - 3 D A C\; +\; 3 x y C - x^2 A y C + A^2 y C + $
![]() $ t y^2 C \; -\; 3 t B C\; +\; D^2 B C\; -\; t x A B C\; -\; D A y B C \; -\; x y^2 B C\; +\; x B^2 C\; +\; A^2 B^2 C - 6 z C+t D z C+$
$ t y^2 C \; -\; 3 t B C\; +\; D^2 B C\; -\; t x A B C\; -\; D A y B C \; -\; x y^2 B C\; +\; x B^2 C\; +\; A^2 B^2 C - 6 z C+t D z C+$
![]() $x A z C+y B z C+t x C^2 + D y C^2 - 2 A B C^2 + C^3.$
$x A z C+y B z C+t x C^2 + D y C^2 - 2 A B C^2 + C^3.$
As functions of the matrix variables
![]() $\mathbf {X}$
and
$\mathbf {X}$
and
![]() $\mathbf {Y}$
(up to the ideal
$\mathbf {Y}$
(up to the ideal
![]() $\langle \mathrm {Det}(\mathbf {X})-1,\mathrm {Det}(\mathbf {Y})-1\rangle$
), the variables
$\langle \mathrm {Det}(\mathbf {X})-1,\mathrm {Det}(\mathbf {Y})-1\rangle$
), the variables
![]() $x,y,z,t, A,B,C,D,s$
are as follows:
$x,y,z,t, A,B,C,D,s$
are as follows:
In these terms, the relations are
and
Remark 2.9. In Lawton [Reference LawtonLaw06, Reference LawtonLaw07] the polynomials
![]() $P,Q$
are shown to have
$P,Q$
are shown to have
![]() $\mathrm {Out}(F_2)$
symmetry and in terms of that symmetry they can be written more compactly. See also Parker [Reference ParkerPar12] for a ‘cyclically’ symmetric coordinate change.
$\mathrm {Out}(F_2)$
symmetry and in terms of that symmetry they can be written more compactly. See also Parker [Reference ParkerPar12] for a ‘cyclically’ symmetric coordinate change.
As shown in Florentino and Lawton [Reference Florentino and LawtonFL09], the singular variety
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
strong deformation retracts to a topological
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
strong deformation retracts to a topological
![]() $8$
-sphere
$8$
-sphere
![]() $S^8$
. In fact, this
$S^8$
. In fact, this
![]() $8$
-sphere is precisely the
$8$
-sphere is precisely the
![]() $\mathrm {SU}(3)$
-character variety of
$\mathrm {SU}(3)$
-character variety of
![]() $F_2$
:
$F_2$
:
![]() $\mathfrak {X}(F_2,\mathrm {SU}(3)):=\mathrm {Hom}(F_2,\mathrm {SU}(3))/\mathrm {SU}(3).$
$\mathfrak {X}(F_2,\mathrm {SU}(3)):=\mathrm {Hom}(F_2,\mathrm {SU}(3))/\mathrm {SU}(3).$
2.4.2
 $\mathrm {SU}(2,1)$
-character variety
$\mathrm {SU}(2,1)$
-character variety
We are interested in the corresponding moduli space where
![]() $\mathrm {SU}(3)$
is replaced by
$\mathrm {SU}(3)$
is replaced by
![]() $\mathrm {SU}(2,1)$
.
$\mathrm {SU}(2,1)$
.
Given a word
![]() $w\in F_2=\langle \alpha, \beta \rangle$
, define
$w\in F_2=\langle \alpha, \beta \rangle$
, define
![]() $\mathrm {tr}_w\!:\!\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))\longrightarrow \mathbb {C}$
by
$\mathrm {tr}_w\!:\!\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))\longrightarrow \mathbb {C}$
by
![]() $\mathrm {tr}_w([\rho ]):=\mathrm {tr}(\rho (w))$
. For representations taking values in
$\mathrm {tr}_w([\rho ]):=\mathrm {tr}(\rho (w))$
. For representations taking values in
![]() $\mathrm {SU}(3)$
or
$\mathrm {SU}(3)$
or
![]() $\mathrm {SU}(2,1)$
, we have that
$\mathrm {SU}(2,1)$
, we have that
![]() $\mathrm {tr}_{w^{-1}}=\overline {\mathrm {tr}_w}$
for any word
$\mathrm {tr}_{w^{-1}}=\overline {\mathrm {tr}_w}$
for any word
![]() $w\in F_2$
. Thus, the real coordinate ring of
$w\in F_2$
. Thus, the real coordinate ring of
![]() $\mathfrak {X}(F_2,\mathrm {SU}(3))$
or the polystable quotient
$\mathfrak {X}(F_2,\mathrm {SU}(3))$
or the polystable quotient
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1)):=\mathrm {Hom}(F_2,\mathrm {SU}(2,1))^*/\mathrm {SU}(2,1)$
is generated by the real and imaginary parts of
$\mathfrak {X}(F_2,\mathrm {SU}(2,1)):=\mathrm {Hom}(F_2,\mathrm {SU}(2,1))^*/\mathrm {SU}(2,1)$
is generated by the real and imaginary parts of
subject to the relations
and
Note that both
![]() $P$
and
$P$
and
![]() $Q$
will be real polynomials, as
$Q$
will be real polynomials, as
![]() $P$
is the sum
$P$
is the sum
while
![]() $Q$
is the product
$Q$
is the product
and hence will simplify to real polynomials in the real and imaginary parts of
![]() $\mathrm {tr}_\alpha, $
$\mathrm {tr}_\alpha, $
![]() $\mathrm {tr}_\beta, $
$\mathrm {tr}_\beta, $
![]() $\mathrm {tr}_{\alpha \beta }$
and
$\mathrm {tr}_{\alpha \beta }$
and
![]() $\mathrm {tr}_{\alpha \beta ^{-1}}$
.
$\mathrm {tr}_{\alpha \beta ^{-1}}$
.
If we write this out in terms of the variables
![]() $x,y,z,t$
above, we obtain for
$x,y,z,t$
above, we obtain for
![]() $P$
and
$P$
and
![]() $Q$
the following expressions:
$Q$
the following expressions:
and
![]() $Q=9 - 6 |x|^2 - 6 | y |^2 - 6 |z|^2 - 6 | t |^2 + | t |^2 | y |^2 +| x |^2 | y |^2+|y|^2 |z|^2 + |t|^2|z|^2 +|x|^2|z|^ 2+ |t|^2|x|^2$
$Q=9 - 6 |x|^2 - 6 | y |^2 - 6 |z|^2 - 6 | t |^2 + | t |^2 | y |^2 +| x |^2 | y |^2+|y|^2 |z|^2 + |t|^2|z|^2 +|x|^2|z|^ 2+ |t|^2|x|^2$
![]() $ +\;|x|^2 |y|^4 \;+\; | y |^2 | x |^4+2 \Re (z^3)\;+\;2 \Re (t^3)+2 \Re(x^3)\;+\; 2 \Re (y^3) \;+\; 2\Re (t x^2 y) - 6 \Re (t x z) + 2 \Re (t^2 y z)\; +$
$ +\;|x|^2 |y|^4 \;+\; | y |^2 | x |^4+2 \Re (z^3)\;+\;2 \Re (t^3)+2 \Re(x^3)\;+\; 2 \Re (y^3) \;+\; 2\Re (t x^2 y) - 6 \Re (t x z) + 2 \Re (t^2 y z)\; +$
![]() $ 2 \Re (x^2 y^2 z) \; -\; 4 \Re (x y z^2)\; +\; 2 \Re (x y^2 \overline {t})\; -\; 6 \Re (y z \overline {t})\; +\; 2 \Re (x z \overline {t}^2)\; +\; 6 \Re (t y \overline {x}) - 2 | x |^2 \Re ( y^3)+2 \Re (y^2 z \overline {x})$
$ 2 \Re (x^2 y^2 z) \; -\; 4 \Re (x y z^2)\; +\; 2 \Re (x y^2 \overline {t})\; -\; 6 \Re (y z \overline {t})\; +\; 2 \Re (x z \overline {t}^2)\; +\; 6 \Re (t y \overline {x}) - 2 | x |^2 \Re ( y^3)+2 \Re (y^2 z \overline {x})$
![]() $ -\; 2 | y |^2 \Re (\overline {x} t y) \;-\;2 | x |^2 \Re ( y z \overline {t}) \;+\; 2 \Re (z^2 \overline {t}\overline {x}) \;-\; 4 \Re ( y \overline {t}^2 \overline {x}) \;-\; 2 | x |^2 \Re (t y \overline {x}) \;+\; 2 \Re (t z \overline {x}^2)\;\;+\;\;2 \Re (y^2 \overline {t} \overline {x}^2)$
$ -\; 2 | y |^2 \Re (\overline {x} t y) \;-\;2 | x |^2 \Re ( y z \overline {t}) \;+\; 2 \Re (z^2 \overline {t}\overline {x}) \;-\; 4 \Re ( y \overline {t}^2 \overline {x}) \;-\; 2 | x |^2 \Re (t y \overline {x}) \;+\; 2 \Re (t z \overline {x}^2)\;\;+\;\;2 \Re (y^2 \overline {t} \overline {x}^2)$
![]() $ -\;2 | y |^2 \Re (x^3) \;+\; 2 \Re (x^2 z \overline {y}) \;-\; 2 | y |^2 \Re (t x z)\;+\;2 \Re (t z^2 \overline {y}) \;+\;6 \Re ( z \overline {x} \overline {y}) \;-\; 2 | x |^2 \Re (z \overline {x} \overline {y}) \;\;+\;\; 2 \Re (z \overline {t}\overline {y}^2)\; -$
$ -\;2 | y |^2 \Re (x^3) \;+\; 2 \Re (x^2 z \overline {y}) \;-\; 2 | y |^2 \Re (t x z)\;+\;2 \Re (t z^2 \overline {y}) \;+\;6 \Re ( z \overline {x} \overline {y}) \;-\; 2 | x |^2 \Re (z \overline {x} \overline {y}) \;\;+\;\; 2 \Re (z \overline {t}\overline {y}^2)\; -$
![]() $ 2 | y |^2 \Re ( z \overline {x} \overline {y}).$
$ 2 | y |^2 \Re ( z \overline {x} \overline {y}).$
However, just because
![]() $\mathfrak {X}(F_2,\mathrm {SU}(3))$
and
$\mathfrak {X}(F_2,\mathrm {SU}(3))$
and
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
satisfy the same real algebraic equations and have the same (real) dimension, it does not mean they are homeomorphic. In fact,
$\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
satisfy the same real algebraic equations and have the same (real) dimension, it does not mean they are homeomorphic. In fact,
![]() $\mathfrak {X}(F_2,\mathrm {SU}(3))\cong S^8$
, and we now show that
$\mathfrak {X}(F_2,\mathrm {SU}(3))\cong S^8$
, and we now show that
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is homotopic to a torus
$\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is homotopic to a torus
![]() $S^1\times S^1$
.
$S^1\times S^1$
.
Theorem 2.10. The character variety
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
strong deformation retracts to
$\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
strong deformation retracts to
![]() $S^1\times S^1$
.
$S^1\times S^1$
.
Proof.
As defined above,
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is the polystable quotient of
$\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is the polystable quotient of
![]() $\mathrm {Hom}(F_2,\mathrm {SU}(2,1))$
by the conjugation action of
$\mathrm {Hom}(F_2,\mathrm {SU}(2,1))$
by the conjugation action of
![]() $\mathrm {SU}(2,1)$
. As Lemma2.4 shows,
$\mathrm {SU}(2,1)$
. As Lemma2.4 shows,
![]() $\mathrm {U}(2)$
is a maximal compact subgroup of
$\mathrm {U}(2)$
is a maximal compact subgroup of
![]() $\mathrm {SU}(2,1)$
. Thus, by Casimiro et al. [Reference Casimiro, Florentino, Lawton and OliveiraCFLO16],
$\mathrm {SU}(2,1)$
. Thus, by Casimiro et al. [Reference Casimiro, Florentino, Lawton and OliveiraCFLO16],
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
strong deformation retracts to
$\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
strong deformation retracts to
![]() $\mathfrak {X}(F_2,\mathrm {U}(2))$
.
$\mathfrak {X}(F_2,\mathrm {U}(2))$
.
On the other hand,
![]() $\mathrm {U}(2)\cong \mathrm {SU}(2)\times _{\mathbb {Z}_2}S^1$
, where
$\mathrm {U}(2)\cong \mathrm {SU}(2)\times _{\mathbb {Z}_2}S^1$
, where
![]() $\mathrm {SU}(2)\times _{\mathbb {Z}_2}S^1 := \left (\mathrm {SU}(2)\times S^1\right )/ \mathbb {Z}_2,$
and where
$\mathrm {SU}(2)\times _{\mathbb {Z}_2}S^1 := \left (\mathrm {SU}(2)\times S^1\right )/ \mathbb {Z}_2,$
and where
![]() $\mathbb {Z}_2$
acts on
$\mathbb {Z}_2$
acts on
![]() $\mathrm {SU}(2)\times S^1$
as follows. For
$\mathrm {SU}(2)\times S^1$
as follows. For
![]() $\mu \in \{\pm 1\}\cong \mathbb {Z}_2$
,
$\mu \in \{\pm 1\}\cong \mathbb {Z}_2$
,
![]() $A \in \mathrm {SU}(2)$
and
$A \in \mathrm {SU}(2)$
and
![]() $\zeta \in S^1$
,
$\zeta \in S^1$
,
![]() $\mu \cdot (A, \zeta ):= (\mu A, \mu ^{-1}\zeta )$
. From this we conclude that
$\mu \cdot (A, \zeta ):= (\mu A, \mu ^{-1}\zeta )$
. From this we conclude that
![]() $\mathfrak {X}(F_2,\mathrm {U}(2))\cong \mathfrak {X}(F_2,\mathrm {SU}(2))\times _{\mathbb {Z}_2^2}(S^1\times S^1)$
by Florentino and Lawton [Reference Florentino and LawtonFL12], where
$\mathfrak {X}(F_2,\mathrm {U}(2))\cong \mathfrak {X}(F_2,\mathrm {SU}(2))\times _{\mathbb {Z}_2^2}(S^1\times S^1)$
by Florentino and Lawton [Reference Florentino and LawtonFL12], where
and the action of
![]() $\mathbb {Z}_2^2$
on
$\mathbb {Z}_2^2$
on
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2))\times (S^1\times S^1)$
is the product action coming from the action of
$\mathfrak {X}(F_2,\mathrm {SU}(2))\times (S^1\times S^1)$
is the product action coming from the action of
![]() $\mathbb {Z}_2$
defined above. On the other hand,
$\mathbb {Z}_2$
defined above. On the other hand,
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2))$
is a closed 3-ball
$\mathfrak {X}(F_2,\mathrm {SU}(2))$
is a closed 3-ball
![]() $B$
(see Florentino and Lawton [Reference Florentino and LawtonFL09]) and so by [Reference Florentino and LawtonFL12] we conclude that
$B$
(see Florentino and Lawton [Reference Florentino and LawtonFL09]) and so by [Reference Florentino and LawtonFL12] we conclude that
![]() $\mathfrak {X}(F_2,\mathrm {U}(2))\cong B\times (S^1\times S^1),$
which strong deformation retracts to
$\mathfrak {X}(F_2,\mathrm {U}(2))\cong B\times (S^1\times S^1),$
which strong deformation retracts to
![]() $S^1\times S^1$
, as required.
$S^1\times S^1$
, as required.
Given that
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
deformation retracts onto
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
deformation retracts onto
![]() $\mathfrak {X}(F_2,\mathrm {SU}(3))$
and
$\mathfrak {X}(F_2,\mathrm {SU}(3))$
and
![]() $\mathfrak {X}(F_2,\mathrm {SU}(3))$
is homeomorphic to an 8-sphere, we have the following corollary.
$\mathfrak {X}(F_2,\mathrm {SU}(3))$
is homeomorphic to an 8-sphere, we have the following corollary.
Corollary 2.11. The character variety
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is not simply connected, and so is not homotopic to either
$\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is not simply connected, and so is not homotopic to either
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
or
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
or
![]() $\mathfrak {X}(F_2,\mathrm {SU}(3))$
.
$\mathfrak {X}(F_2,\mathrm {SU}(3))$
.
We will be studying the mapping class group dynamics on certain subvarieties of
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
, called relative character varieties. To shorten the notation, let
$\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
, called relative character varieties. To shorten the notation, let
![]() $\mathfrak {X}=\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
in what follows. Define
$\mathfrak {X}=\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
in what follows. Define
![]() $\mathfrak {b}:\mathfrak {X}\longrightarrow \mathbb {C}$
by
$\mathfrak {b}:\mathfrak {X}\longrightarrow \mathbb {C}$
by
![]() $\mathfrak {b}([\rho ])=\mathrm {tr}(\rho (\alpha \beta \alpha ^{-1}\beta ^{-1}))$
. By [Reference GoldmanGol99, Theorem 6.2.4],
$\mathfrak {b}([\rho ])=\mathrm {tr}(\rho (\alpha \beta \alpha ^{-1}\beta ^{-1}))$
. By [Reference GoldmanGol99, Theorem 6.2.4],
![]() $\mathfrak {b}$
is surjective.
$\mathfrak {b}$
is surjective.
Definition 2.12. The relative character variety with respect to
![]() $c\in \mathbb {C}$
is
$c\in \mathbb {C}$
is
![]() $\mathfrak {X}_c:=\mathfrak {b}^{-1}(c)$
.
$\mathfrak {X}_c:=\mathfrak {b}^{-1}(c)$
.
Theorem 2.13. The number
![]() $c\in \mathbb {C}-\mathbb {R}$
if and only if
$c\in \mathbb {C}-\mathbb {R}$
if and only if
![]() $P^2-4Q\not=0$
.
$P^2-4Q\not=0$
.
![]() $\mathfrak {X}_c$
is a smooth manifold if
$\mathfrak {X}_c$
is a smooth manifold if
![]() $c\in \mathbb {C}-\mathbb {R}$
.
$c\in \mathbb {C}-\mathbb {R}$
.
Proof.
The variety
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is a branched double cover of
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
is a branched double cover of
![]() $\mathbb {C}^8$
embedded in
$\mathbb {C}^8$
embedded in
![]() $\mathbb {C}^9$
as described in Section 2.4.1. The branching locus
$\mathbb {C}^9$
as described in Section 2.4.1. The branching locus
![]() $\mathcal {B}$
, where the branched double cover is exactly one-to-one, is defined by the equation
$\mathcal {B}$
, where the branched double cover is exactly one-to-one, is defined by the equation
![]() $P^2-4Q=0$
. As shown in Florentino and Lawton [Reference Florentino and LawtonFL09], the locus
$P^2-4Q=0$
. As shown in Florentino and Lawton [Reference Florentino and LawtonFL09], the locus
![]() $\mathcal {B}$
corresponds exactly to the representations that are fixed under the involution
$\mathcal {B}$
corresponds exactly to the representations that are fixed under the involution
![]() $[(A,B)]\mapsto [(A^\dagger, B^\dagger )]$
. We call these the symmetric representations (up to conjugation). Equations (1) and (2) imply that
$[(A,B)]\mapsto [(A^\dagger, B^\dagger )]$
. We call these the symmetric representations (up to conjugation). Equations (1) and (2) imply that
![]() $\mathfrak {X}_c\subset \mathcal {B}$
if and only if
$\mathfrak {X}_c\subset \mathcal {B}$
if and only if
![]() $c\in \mathbb {R}$
. Equivalently,
$c\in \mathbb {R}$
. Equivalently,
![]() $\mathfrak {X}_c\cap \mathcal {B}=\emptyset$
if and only if
$\mathfrak {X}_c\cap \mathcal {B}=\emptyset$
if and only if
![]() $c\in \mathbb {C}-\mathbb {R}$
. As shown in Lawton [Reference LawtonLaw06, Reference LawtonLaw07], the reducible locus (that is, the set of reducible representations) is contained in the branching locus. Thus, if
$c\in \mathbb {C}-\mathbb {R}$
. As shown in Lawton [Reference LawtonLaw06, Reference LawtonLaw07], the reducible locus (that is, the set of reducible representations) is contained in the branching locus. Thus, if
![]() $c\in \mathbb {C}-\mathbb {R}$
, we know that
$c\in \mathbb {C}-\mathbb {R}$
, we know that
![]() $\mathfrak {X}_c$
consists of conjugation classes of irreducible representations. The irreducible locus is a smooth manifold in
$\mathfrak {X}_c$
consists of conjugation classes of irreducible representations. The irreducible locus is a smooth manifold in
![]() $\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
by [Reference LawtonLaw07], which implies that the irreducible locus in
$\mathfrak {X}(F_2,\mathrm {SL}(3,\mathbb {C}))$
by [Reference LawtonLaw07], which implies that the irreducible locus in
![]() $\mathfrak {X}$
is a smooth manifold too. Thus, since the boundary map is a submersion on the irreducible locus (as the computation in Goldman, Lawton and Xia [Reference Goldman, Lawton and XiaGLX21, Proposition 8.1] applies to this setting too), the fibers
$\mathfrak {X}$
is a smooth manifold too. Thus, since the boundary map is a submersion on the irreducible locus (as the computation in Goldman, Lawton and Xia [Reference Goldman, Lawton and XiaGLX21, Proposition 8.1] applies to this setting too), the fibers
![]() $\mathfrak {X}_c$
are smooth submanifolds by the inverse function theorem.
$\mathfrak {X}_c$
are smooth submanifolds by the inverse function theorem.
Remark 2.14. The locus of reducible representations (which are generally singular) is a five-dimensional subspace of the seven-dimensional branching locus in
![]() $\mathfrak {X}$
. Thus, if
$\mathfrak {X}$
. Thus, if
![]() $c\in \mathbb {R}$
, and so
$c\in \mathbb {R}$
, and so
![]() $\mathfrak {X}_c$
is in the branching locus, we expect that
$\mathfrak {X}_c$
is in the branching locus, we expect that
![]() $\mathfrak {X}_c$
contains singular representations and so is not a manifold. Heuristically this should follow since either
$\mathfrak {X}_c$
contains singular representations and so is not a manifold. Heuristically this should follow since either
![]() $\mathfrak {X}_c$
contains both an irreducible and a reducible and thus a singularity, or
$\mathfrak {X}_c$
contains both an irreducible and a reducible and thus a singularity, or
![]() $\mathfrak {X}_c$
contains only reducibles and thus contains an orbifold singularity from the action of the Weyl group. However, as [Reference Forni, Goldman, Lawton and MatheusFGLM22, Proposition 3.1] shows, relative character varieties containing only reducible representations can ‘accidentally’ be manifolds. We also note that irreducible representations in the branching locus may have special geometric features, as described by Paupert and Will [Reference Paupert and WillPW17] or Will [Reference WillWil07].
$\mathfrak {X}_c$
contains only reducibles and thus contains an orbifold singularity from the action of the Weyl group. However, as [Reference Forni, Goldman, Lawton and MatheusFGLM22, Proposition 3.1] shows, relative character varieties containing only reducible representations can ‘accidentally’ be manifolds. We also note that irreducible representations in the branching locus may have special geometric features, as described by Paupert and Will [Reference Paupert and WillPW17] or Will [Reference WillWil07].
Remark 2.15. It would be interesting to explore whether
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is a topological manifold, since
$\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is a topological manifold, since
![]() $\mathfrak {X}(F_2,\mathrm {SU}(3))$
is a topological manifold and
$\mathfrak {X}(F_2,\mathrm {SU}(3))$
is a topological manifold and
![]() $\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is homotopic to a manifold. It would also be interesting to explore the topology
$\mathfrak {X}(F_2,\mathrm {SU}(2,1))$
is homotopic to a manifold. It would also be interesting to explore the topology
![]() $($
up to homotopy
$($
up to homotopy
![]() $)$
of the level sets
$)$
of the level sets
![]() $\mathfrak {X}_c$
for various values of
$\mathfrak {X}_c$
for various values of
![]() $c\in \mathbb {C}$
.
$c\in \mathbb {C}$
.
In our situation,
![]() $\mathrm {Out}(F_2)\cong \mathrm {GL}(2,\mathbb {Z})$
which is isomorphic to the mapping class group of the one-holed torus. This group acts on
$\mathrm {Out}(F_2)\cong \mathrm {GL}(2,\mathbb {Z})$
which is isomorphic to the mapping class group of the one-holed torus. This group acts on
![]() $\mathfrak {X}$
and the subgroup of mapping classes that fix the boundary of
$\mathfrak {X}$
and the subgroup of mapping classes that fix the boundary of
![]() $S_{1,1}$
acts on
$S_{1,1}$
acts on
![]() $\mathfrak {X}_c$
. We will now proceed to show that there exists an open domain of discontinuity
$\mathfrak {X}_c$
. We will now proceed to show that there exists an open domain of discontinuity
![]() $\mathfrak {X}_{BQ}$
for the action of
$\mathfrak {X}_{BQ}$
for the action of
![]() $\mathrm {Out}(F_2)$
on
$\mathrm {Out}(F_2)$
on
![]() $\mathfrak {X}$
which strictly contains the set of discrete, faithful, convex cocompact representations (more generally the primitive stable representations).
$\mathfrak {X}$
which strictly contains the set of discrete, faithful, convex cocompact representations (more generally the primitive stable representations).
3. Bowditch set
Recall that the aim of this article is to define a set of representations that will provide an open domain of discontinuity for the action of
![]() $\mathrm {Out}(F_2)$
on
$\mathrm {Out}(F_2)$
on
![]() $\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. In particular, in this section we will define and study the set of Bowditch representations, and in the next section we will prove that they define an open domain of discontinuity.
$\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. In particular, in this section we will define and study the set of Bowditch representations, and in the next section we will prove that they define an open domain of discontinuity.
For notational convenience, given a representation
![]() $\rho \colon \thinspace F_2 \rightarrow \mathrm {SU}(2,1)$
, or its conjugacy class
$\rho \colon \thinspace F_2 \rightarrow \mathrm {SU}(2,1)$
, or its conjugacy class
![]() $[\rho ] \in \mathfrak {X}$
, and given
$[\rho ] \in \mathfrak {X}$
, and given
![]() $X, Y \in \mathcal {S}$
, we will write
$X, Y \in \mathcal {S}$
, we will write
![]() $x=\textrm {tr }(\rho (X))$
,
$x=\textrm {tr }(\rho (X))$
,
![]() $y=\textrm {tr }(\rho (Y))$
etc.
$y=\textrm {tr }(\rho (Y))$
etc.
3.1 Orientation on
 $\mathcal {E}$
$\mathcal {E}$
Given a representation
![]() $\rho \colon \thinspace F_2 \rightarrow \mathrm {SU}(2,1)$
, we will need to assign to each undirected edge
$\rho \colon \thinspace F_2 \rightarrow \mathrm {SU}(2,1)$
, we will need to assign to each undirected edge
![]() $e \in \mathcal {E}$
a particular directed edge
$e \in \mathcal {E}$
a particular directed edge
![]() $\vec e_\rho$
. In Section 2.2 we identified edges
$\vec e_\rho$
. In Section 2.2 we identified edges
![]() $e$
of
$e$
of
![]() $\mathcal {E}$
with triples
$\mathcal {E}$
with triples
![]() $e = (X; Y, Z) \in \mathcal {E}^{(1)}$
where
$e = (X; Y, Z) \in \mathcal {E}^{(1)}$
where
![]() $X,Y,Z \in \mathcal {S}$
. Since we need to discuss an orientation, it will be more useful to use the notation
$X,Y,Z \in \mathcal {S}$
. Since we need to discuss an orientation, it will be more useful to use the notation
![]() $e = (X, Y, Z; T, T') \in \mathcal {E}^{(1)}$
; see Figure 2.
$e = (X, Y, Z; T, T') \in \mathcal {E}^{(1)}$
; see Figure 2.
Definition 3.1. Let
![]() $e= (X, Y, Z; T, T') \in \mathcal {E}^{(1)}$
. Let
$e= (X, Y, Z; T, T') \in \mathcal {E}^{(1)}$
. Let
![]() $t = |\mathrm {tr} (\rho (T)) |$
and
$t = |\mathrm {tr} (\rho (T)) |$
and
![]() $|\mathrm {tr} (\rho (T'))| = t'$
. Then we define the oriented edge
$|\mathrm {tr} (\rho (T'))| = t'$
. Then we define the oriented edge
![]() $\vec e_\rho$
in the following way:
$\vec e_\rho$
in the following way:
-
if
 $|t| \gt |t'|$
(respectively,
$|t| \gt |t'|$
(respectively,
 $|t| \lt |t'|$
) we orient the edge
$|t| \lt |t'|$
) we orient the edge
 $e$
pointing towards
$e$
pointing towards
 $T'$
(respectively, towards
$T'$
(respectively, towards
 $T$
);
$T$
); -
if
 $|t| = |t'|$
we choose the orientation of
$|t| = |t'|$
we choose the orientation of
 $\vec e_\rho$
arbitrarily.
$\vec e_\rho$
arbitrarily.
That oriented edge is denoted by
![]() $\vec e_\rho = (X, Y, Z; T \rightarrow T')$
, when it points towards
$\vec e_\rho = (X, Y, Z; T \rightarrow T')$
, when it points towards
![]() $T'$
.
$T'$
.
We will see that the intersection of the Bowditch representations (up to conjugation) with the set of representations that satisfy
![]() $|t| = |t'|$
for infinitely many edges is empty. So, for a given representation, the finite number of arbitrary choices that occur when
$|t| = |t'|$
for infinitely many edges is empty. So, for a given representation, the finite number of arbitrary choices that occur when
![]() $|t| = |t'|$
will not affect the large-scale behavior of the orientation of the graph
$|t| = |t'|$
will not affect the large-scale behavior of the orientation of the graph
![]() $\mathcal {E}$
, the latter being what is essential to our proof.
$\mathcal {E}$
, the latter being what is essential to our proof.
3.2 Connectedness and the Fork Lemma
In this subsection we will prove an important lemma, called the ‘Fork Lemma’, which will be the key to proving the connectedness of the set of regions with trace bounded by a given constant.
3.2.1 Fork Lemma
Let us first describe a preliminary result which will be useful in several proofs in this section and in Section 4.
Lemma 3.2.
Let
![]() $c \in \mathbb {C}$
,
$c \in \mathbb {C}$
,
![]() $[\rho ] \in \mathfrak {X}_c$
,
$[\rho ] \in \mathfrak {X}_c$
,
![]() $C=\max \{2\sqrt [4]{3},\sqrt {|\Re (c)|}\}$
and
$C=\max \{2\sqrt [4]{3},\sqrt {|\Re (c)|}\}$
and
![]() $v=(X,Y;Z,T) \in \mathcal {E}^{(0)}$
. If the collection
$v=(X,Y;Z,T) \in \mathcal {E}^{(0)}$
. If the collection
![]() $x$
,
$x$
,
![]() $y$
,
$y$
,
![]() $z$
and
$z$
and
![]() $t$
satisfies
$t$
satisfies
![]() $|x|,|y| \geqslant C$
and
$|x|,|y| \geqslant C$
and
![]() $|t| \geqslant |z|$
, then we have
$|t| \geqslant |z|$
, then we have
Proof.
Without loss of generality, we can assume that
![]() $|x| \geqslant |y|\geqslant C$
. For the first inequality, assume by contradiction that
$|x| \geqslant |y|\geqslant C$
. For the first inequality, assume by contradiction that
![]() $|t| \leqslant \frac {C}{4}|x|$
. Recall that
$|t| \leqslant \frac {C}{4}|x|$
. Recall that
We have
 \begin{align*} P & \geqslant (|x|^2|y|^2 - 4|x||y||t| +|t|^2) + |x|^2 + |y|^2 + |z|^2 -3 \\ & \geqslant \left ((|xy| - 2 |t|)^2 - 3|t|^2\right ) + 2C^2+0 - 3 \\ & \geqslant \left (\left (|x||y| - \frac {C}{2} |x|\right )^2 - \frac {3}{16} C^2 |x|^2\right ) + 2C^2 - 3 \\ & = |x|^2 \left ( \left (|y|-\frac {C}{2}\right )^2 - \frac {3}{16}C^2\right ) + 2C^2 - 3 \\ & \geqslant C^2 \frac {C^2}{16} + 2C^2 - 3 \gt 2C^2, \end{align*}
\begin{align*} P & \geqslant (|x|^2|y|^2 - 4|x||y||t| +|t|^2) + |x|^2 + |y|^2 + |z|^2 -3 \\ & \geqslant \left ((|xy| - 2 |t|)^2 - 3|t|^2\right ) + 2C^2+0 - 3 \\ & \geqslant \left (\left (|x||y| - \frac {C}{2} |x|\right )^2 - \frac {3}{16} C^2 |x|^2\right ) + 2C^2 - 3 \\ & = |x|^2 \left ( \left (|y|-\frac {C}{2}\right )^2 - \frac {3}{16}C^2\right ) + 2C^2 - 3 \\ & \geqslant C^2 \frac {C^2}{16} + 2C^2 - 3 \gt 2C^2, \end{align*}
where we used the hypothesis
![]() $|t| \leqslant \frac {C}{4}|x|$
only in the third line, and the fact that
$|t| \leqslant \frac {C}{4}|x|$
only in the third line, and the fact that
![]() $C^4 \gt 16 \cdot 3$
in the last inequality. This gives a contradiction, as
$C^4 \gt 16 \cdot 3$
in the last inequality. This gives a contradiction, as
![]() $ 2\Re (c) \leqslant 2 C^2$
, and hence proves the first inequality.
$ 2\Re (c) \leqslant 2 C^2$
, and hence proves the first inequality.
For the second inequality, assume by contradiction that
![]() $|t| \geqslant 5 |x| |y|$
(or equivalently
$|t| \geqslant 5 |x| |y|$
(or equivalently
![]() $|x| |y| \leqslant \frac {|t|}{5}$
). In that case, we have
$|x| |y| \leqslant \frac {|t|}{5}$
). In that case, we have
 \begin{align*} P & \geqslant (|x|^2|y|^2)+(|x|^2+|y|^2)+(|z|^2)+(|t|^2-2 |x||y||t| - 2 |x||y||z|) - 3 \\ & \geqslant C^4+2C^2+0 + \frac {|t|^2}{5} - 3 \\ & \gt 2C^2, \end{align*}
\begin{align*} P & \geqslant (|x|^2|y|^2)+(|x|^2+|y|^2)+(|z|^2)+(|t|^2-2 |x||y||t| - 2 |x||y||z|) - 3 \\ & \geqslant C^4+2C^2+0 + \frac {|t|^2}{5} - 3 \\ & \gt 2C^2, \end{align*}
where the last inequality is justified since
![]() $C^4 \gt 16\cdot 3 \gt 3$
. This gives the same contradiction, as
$C^4 \gt 16\cdot 3 \gt 3$
. This gives the same contradiction, as
![]() $P \leqslant 2 C^2$
.
$P \leqslant 2 C^2$
.
We are now ready to state and prove the Fork Lemma. First, let us define what is a fork. For a vertex
![]() $v = (X, Y ; Z, T) \in \mathcal {E}^0$
choose representatives
$v = (X, Y ; Z, T) \in \mathcal {E}^0$
choose representatives
![]() $\alpha, \beta \in F_2$
of
$\alpha, \beta \in F_2$
of
![]() $X$
and
$X$
and
![]() $Y$
such that
$Y$
such that
![]() $\alpha \beta$
and
$\alpha \beta$
and
![]() $\alpha \beta ^{-1}$
are representatives of
$\alpha \beta ^{-1}$
are representatives of
![]() $Z$
and
$Z$
and
![]() $T$
, respectively. Recall that the traces of the four neighboring regions around
$T$
, respectively. Recall that the traces of the four neighboring regions around
![]() $v$
are given by
$v$
are given by
and
Recall also that we have a
![]() $4$
-coloring of the edges of
$4$
-coloring of the edges of
![]() $\mathcal {E}$
defined in Section 2.2, and at each vertex there are only two triangles of two different colors meeting.
$\mathcal {E}$
defined in Section 2.2, and at each vertex there are only two triangles of two different colors meeting.
Definition 3.3. We say that a vertex
![]() $v \in \mathcal {E}^{(0)}$
is a fork for
$v \in \mathcal {E}^{(0)}$
is a fork for
![]() $\rho$
if there are (at least) two edges oriented by
$\rho$
if there are (at least) two edges oriented by
![]() $\rho$
having
$\rho$
having
![]() $v$
as a source and they are of different colors (for the 4-coloring). Visually,
$v$
as a source and they are of different colors (for the 4-coloring). Visually,
![]() $v$
is a fork if two arrows point away from
$v$
is a fork if two arrows point away from
![]() $v$
in two different triangles. See Figure 5.
$v$
in two different triangles. See Figure 5.

Figure 5. A vertex which is a fork (left) and one which is not (right). The two arrows pointing away from the vertex have to be in different triangles to get a fork.
Equivalently, the vertex
![]() $v = (X, Y ; Z, T) \in \mathcal {E}^{(0)}$
is a fork for
$v = (X, Y ; Z, T) \in \mathcal {E}^{(0)}$
is a fork for
![]() $\rho$
if the following conditions hold:
$\rho$
if the following conditions hold:
 \begin{equation*}\begin{cases}|\textrm {tr }\rho (XY^{-1}) | & \lt \max \{ |\textrm {tr } \rho (XY^2) |, |\textrm {tr } \rho (X^2Y) | \} \\ & \mbox { and } \\ |\textrm {tr } \rho (XY)| & \lt \max \{ |\textrm {tr } \rho (XY^{-2}) |, |\textrm {tr } \rho (X^{-2}Y) | \}.\end{cases}\end{equation*}
\begin{equation*}\begin{cases}|\textrm {tr }\rho (XY^{-1}) | & \lt \max \{ |\textrm {tr } \rho (XY^2) |, |\textrm {tr } \rho (X^2Y) | \} \\ & \mbox { and } \\ |\textrm {tr } \rho (XY)| & \lt \max \{ |\textrm {tr } \rho (XY^{-2}) |, |\textrm {tr } \rho (X^{-2}Y) | \}.\end{cases}\end{equation*}
In terms of the four traces
![]() $(x,y,z,t)$
these conditions can be written as
$(x,y,z,t)$
these conditions can be written as
 \begin{equation*}\begin{cases} |t| \lt |t- x \overline y+yz| \\ or \\ |t| \lt |t - x \overline {y} + \overline {xz}|, \end{cases} \quad \mbox { and } \begin{cases} |z| \lt |z-xy+\overline {xt}| \\ or \\ |z| \lt |z - xy + \overline {y}t |. \end{cases} \end{equation*}
\begin{equation*}\begin{cases} |t| \lt |t- x \overline y+yz| \\ or \\ |t| \lt |t - x \overline {y} + \overline {xz}|, \end{cases} \quad \mbox { and } \begin{cases} |z| \lt |z-xy+\overline {xt}| \\ or \\ |z| \lt |z - xy + \overline {y}t |. \end{cases} \end{equation*}
We will call these inequalities the fork conditions. See Figure 6.
Lemma 3.4.
Let
![]() $c \in \mathbb {C}$
,
$c \in \mathbb {C}$
,
![]() $[\rho ] \in \mathfrak {X}_c$
and
$[\rho ] \in \mathfrak {X}_c$
and
![]() $v = (X,Y) \in \mathcal {E}^{(0)}$
. If
$v = (X,Y) \in \mathcal {E}^{(0)}$
. If
![]() $v$
is a fork for
$v$
is a fork for
![]() $\rho$
, then we have that
$\rho$
, then we have that
![]() $\min \{|x|, |y| \} \leqslant \max \{6,\sqrt {|\Re (c)|}\}$
.
$\min \{|x|, |y| \} \leqslant \max \{6,\sqrt {|\Re (c)|}\}$
.
Proof.
Without loss of generality, and by using the fork conditions, we can assume that
![]() $|t| \gt | t - x\bar y+yz |$
and
$|t| \gt | t - x\bar y+yz |$
and
![]() $|z| \gt |z -xy +\overline {xt}|$
. Let
$|z| \gt |z -xy +\overline {xt}|$
. Let
![]() $C = \max \{6,\sqrt {|\Re (c)|}\}$
and assume by contradiction that
$C = \max \{6,\sqrt {|\Re (c)|}\}$
and assume by contradiction that
![]() $\min \{|x|,|y|\} \gt C \geqslant 6$
.
$\min \{|x|,|y|\} \gt C \geqslant 6$
.

Figure 6. A fork with the labeling of the neighboring regions.
Note that
![]() $|t - x\bar y+yz | \geqslant |yz-x\bar y|-|t| \geqslant |y||z|-|x||y| - |t|$
. So, since we have
$|t - x\bar y+yz | \geqslant |yz-x\bar y|-|t| \geqslant |y||z|-|x||y| - |t|$
. So, since we have
![]() $|t| \gt | t - x\bar y+yz|$
by the fork assumption, we deduce that
$|t| \gt | t - x\bar y+yz|$
by the fork assumption, we deduce that
![]() $2|t| +|x||y| \gt |y||z|$
, and hence we obtain
$2|t| +|x||y| \gt |y||z|$
, and hence we obtain
Similarly, as
![]() $|z -xy +\overline {xt} | \geqslant |\overline {tx}-xy|-|z| \geqslant |t||x|-|x||y|- |z|$
and
$|z -xy +\overline {xt} | \geqslant |\overline {tx}-xy|-|z| \geqslant |t||x|-|x||y|- |z|$
and
![]() $|z| \gt |z -xy +\overline {xt}|$
, we get
$|z| \gt |z -xy +\overline {xt}|$
, we get
We combine both inequalities to get
 \begin{align*} |z|+|t| & \lt 2 \left ( \frac {|t|}{|y|} + \frac {|z|}{|x|} \right ) + (|x| + |y|)\\ & \lt 2 \frac {|t| + |z|}{C} + 2\max \{ |x|, |y| \}. \end{align*}
\begin{align*} |z|+|t| & \lt 2 \left ( \frac {|t|}{|y|} + \frac {|z|}{|x|} \right ) + (|x| + |y|)\\ & \lt 2 \frac {|t| + |z|}{C} + 2\max \{ |x|, |y| \}. \end{align*}
From this it follows that
Recall that we have
Since
![]() $C \geqslant 6$
, we have that
$C \geqslant 6$
, we have that
![]() $\frac {4C}{C-2} \leqslant C \lt \min \{|x|,|y|\}$
. Hence, using the inequality above, we get
$\frac {4C}{C-2} \leqslant C \lt \min \{|x|,|y|\}$
. Hence, using the inequality above, we get
 \begin{eqnarray*} |2 \Re (xy\overline z ) + 2 \Re (x \overline y t )| \leqslant 2 |xy| (|z| + |t|) & \lt & \frac {4C}{C-2} |xy| \max \{|x|, |y|\}\\ & \lt & |xy| \min \{|x|, |y|\} \max \{|x|, |y|\} = |x|^2 |y|^2. \end{eqnarray*}
\begin{eqnarray*} |2 \Re (xy\overline z ) + 2 \Re (x \overline y t )| \leqslant 2 |xy| (|z| + |t|) & \lt & \frac {4C}{C-2} |xy| \max \{|x|, |y|\}\\ & \lt & |xy| \min \{|x|, |y|\} \max \{|x|, |y|\} = |x|^2 |y|^2. \end{eqnarray*}
Moreover, using Lemma3.2, we can see that
This implies that
This gives a contradiction, as
![]() $P=2 \Re (c) \leqslant 2 C^2$
.
$P=2 \Re (c) \leqslant 2 C^2$
.
As we will see, the conclusion of the Fork Lemma (Lemma3.4) still holds for vertices that satisfy the fork conditions ‘up to epsilon’, and for certain arguments we will need the notion of an
![]() $\varepsilon$
-fork. More precisely, we give the following definition.
$\varepsilon$
-fork. More precisely, we give the following definition.
Definition 3.5. Let
![]() $\varepsilon \gt 0$
. A vertex
$\varepsilon \gt 0$
. A vertex
![]() $v \in \mathcal {E}$
is an
$v \in \mathcal {E}$
is an
![]() $\varepsilon$
-fork if changing the value of one of the four regions around
$\varepsilon$
-fork if changing the value of one of the four regions around
![]() $v$
by less than
$v$
by less than
![]() $\varepsilon$
makes it a fork. This means that
$\varepsilon$
makes it a fork. This means that
![]() $v$
has (at least) two arrows pointing away from it or pointing towards it, but such that the difference between the values at the opposing regions of the edge, say
$v$
has (at least) two arrows pointing away from it or pointing towards it, but such that the difference between the values at the opposing regions of the edge, say
![]() $x, x' \in \mathbb {C}$
, are such that
$x, x' \in \mathbb {C}$
, are such that
![]() $\vert \vert x \vert - \vert x' \vert \vert \lt \varepsilon$
.
$\vert \vert x \vert - \vert x' \vert \vert \lt \varepsilon$
.
The Fork Lemma (Lemma3.4) above can be generalized to
![]() $\varepsilon$
-forks.
$\varepsilon$
-forks.
Corollary 3.6.
Let
![]() $c \in \mathbb {C}$
,
$c \in \mathbb {C}$
,
![]() $[\rho ] \in \mathfrak {X}_c$
and
$[\rho ] \in \mathfrak {X}_c$
and
![]() $v = (X,Y) \in \mathcal {E}^{(0)}$
. Let
$v = (X,Y) \in \mathcal {E}^{(0)}$
. Let
![]() $C = \max \{6,\sqrt {|\Re (c)|}\}$
and
$C = \max \{6,\sqrt {|\Re (c)|}\}$
and
![]() $\varepsilon _0 = \varepsilon _0(C) = C^2 \frac {C-6}{4} \gt 0$
. For all
$\varepsilon _0 = \varepsilon _0(C) = C^2 \frac {C-6}{4} \gt 0$
. For all
![]() $\varepsilon \lt \varepsilon _0$
, if
$\varepsilon \lt \varepsilon _0$
, if
![]() $v$
is an
$v$
is an
![]() $\varepsilon$
-fork, then
$\varepsilon$
-fork, then
![]() $\min \{ |x|, |y| \} \lt C$
.
$\min \{ |x|, |y| \} \lt C$
.
Proof.
We will follow an argument similar to the one used to prove the Fork Lemma (Lemma3.4). Assume by contradiction that
![]() $\min \{|x|,|y|\} \gt C \geqslant 6$
. Let
$\min \{|x|,|y|\} \gt C \geqslant 6$
. Let
![]() $\varepsilon \lt \varepsilon _0$
. Assume
$\varepsilon \lt \varepsilon _0$
. Assume
![]() $v$
is an
$v$
is an
![]() $\varepsilon$
-fork. We keep the same notation for
$\varepsilon$
-fork. We keep the same notation for
![]() $x,y,z,t$
as before. The fork conditions give
$x,y,z,t$
as before. The fork conditions give
![]() $|t| \gt |t - x \overline y+yz | - \varepsilon$
and
$|t| \gt |t - x \overline y+yz | - \varepsilon$
and
![]() $|z| \gt |z - xy + \overline {xt} | - \varepsilon$
. The same steps as before give
$|z| \gt |z - xy + \overline {xt} | - \varepsilon$
. The same steps as before give
We combine both inequalities and obtain
As
![]() $\varepsilon \lt \varepsilon _0$
, we obtain directly that
$\varepsilon \lt \varepsilon _0$
, we obtain directly that
![]() $|z|+|t| \lt \dfrac {|C|}{2} \max \{|x|,|y|\}$
, since
$|z|+|t| \lt \dfrac {|C|}{2} \max \{|x|,|y|\}$
, since
![]() $C \lt \max \{|x|,|y|\}$
.
$C \lt \max \{|x|,|y|\}$
.
Now, using the hypothesis
![]() $C \lt \min \{ |x|, |y| \}$
, we get
$C \lt \min \{ |x|, |y| \}$
, we get
Using reasoning similar to the previous proof, we can then see that
![]() $P \gt 2C^2$
, which gives a contradiction. So we have that
$P \gt 2C^2$
, which gives a contradiction. So we have that
![]() $\min \{ |x|, |y| \} \leqslant C$
, as we wanted to prove.
$\min \{ |x|, |y| \} \leqslant C$
, as we wanted to prove.
3.2.2 Connectedness
Recall that we have the following identification
![]() $\Omega = \mathcal {C}^{(0)} = \mathcal {S}$
.
$\Omega = \mathcal {C}^{(0)} = \mathcal {S}$
.
For any
![]() $K \geqslant 0$
and
$K \geqslant 0$
and
![]() $[\rho ] \in \mathfrak {X}$
, we denote by
$[\rho ] \in \mathfrak {X}$
, we denote by
![]() $\Omega _\rho (K)$
the set of regions with traces smaller than
$\Omega _\rho (K)$
the set of regions with traces smaller than
![]() $K$
:
$K$
:
Since every element
![]() $\gamma \in \Omega$
corresponds to the closure of a region in the complement of the (properly embedded trivalent) tree
$\gamma \in \Omega$
corresponds to the closure of a region in the complement of the (properly embedded trivalent) tree
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\mathbf {H}^2$
, as defined in Section 2.2, we consider the set
$\mathbf {H}^2$
, as defined in Section 2.2, we consider the set
![]() $\Omega _\rho (K)$
to be a subset of
$\Omega _\rho (K)$
to be a subset of
![]() $\mathbf {H}^2$
. Using the Fork Lemma, in this section we deduce that, for
$\mathbf {H}^2$
. Using the Fork Lemma, in this section we deduce that, for
![]() $K$
large enough, these sets are connected when represented as subsets of
$K$
large enough, these sets are connected when represented as subsets of
![]() $\mathbf {H}^2$
.
$\mathbf {H}^2$
.
Lemma 3.7.
Let
![]() $c \in \mathbb {C}$
and
$c \in \mathbb {C}$
and
![]() $[\rho ] \in \mathfrak {X}_c$
. For all
$[\rho ] \in \mathfrak {X}_c$
. For all
![]() $C \geqslant \max \{6,\sqrt {|\Re (c)|}\}$
, the set
$C \geqslant \max \{6,\sqrt {|\Re (c)|}\}$
, the set
![]() $\Omega _\rho (C)$
is connected.
$\Omega _\rho (C)$
is connected.
Proof.
Assume by contradiction that
![]() $\Omega _\rho (C)$
is not connected. We make an argument based on the minimal distance between two connected components of
$\Omega _\rho (C)$
is not connected. We make an argument based on the minimal distance between two connected components of
![]() $\Omega _\rho (C)$
. Recall that if
$\Omega _\rho (C)$
. Recall that if
![]() $v = (X,Y ; Z, T) \in \mathcal {E}^{(0)}$
, then we have
$v = (X,Y ; Z, T) \in \mathcal {E}^{(0)}$
, then we have
which implies
![]() $P \leqslant 2C^2$
.
$P \leqslant 2C^2$
.
If the distance is
![]() $1$
, then we have a vertex
$1$
, then we have a vertex
![]() $v = (X, Y; Z,T) \in \mathcal {E}^{(0)}$
such that
$v = (X, Y; Z,T) \in \mathcal {E}^{(0)}$
such that
![]() $|z|, |t| \leqslant C$
and
$|z|, |t| \leqslant C$
and
![]() $|x|, |y| \gt C$
. In that case, we have
$|x|, |y| \gt C$
. In that case, we have
since
![]() $5C \lt C^2 \lt |x||y|$
and since
$5C \lt C^2 \lt |x||y|$
and since
![]() $C |x||y| \geqslant C^3 \gt 3$
. This gives
$C |x||y| \geqslant C^3 \gt 3$
. This gives
which is a contradiction.
If the distance is
![]() $2$
, then we have an edge
$2$
, then we have an edge
![]() $(X,Y,T ; Z, Z')$
. We can assume, without loss of generality, that
$(X,Y,T ; Z, Z')$
. We can assume, without loss of generality, that
![]() $|z| \leqslant C$
,
$|z| \leqslant C$
,
![]() $|z'| = |z+\overline {yt} - xy| \leqslant C$
and
$|z'| = |z+\overline {yt} - xy| \leqslant C$
and
![]() $|x|, |y|, |t| \gt C$
. In that case the inequality
$|x|, |y|, |t| \gt C$
. In that case the inequality
![]() $|z+\overline {y}t - xy| \leqslant C$
implies that
$|z+\overline {y}t - xy| \leqslant C$
implies that
![]() $C \lt |t| \leqslant \frac {C+|z|}{|y|} + |x| \lt |x| + 2.$
This gives
$C \lt |t| \leqslant \frac {C+|z|}{|y|} + |x| \lt |x| + 2.$
This gives
where the last inequality follows from
Since
![]() $|t|^2-3\gt C^2-3 \gt 0$
and
$|t|^2-3\gt C^2-3 \gt 0$
and
![]() $|x|^2 + |y|^2 +|z|^2\gt 2 C^2$
, we also find that
$|x|^2 + |y|^2 +|z|^2\gt 2 C^2$
, we also find that
![]() $P\gt 2C^2$
, which gives the same contradiction.
$P\gt 2C^2$
, which gives the same contradiction.
If the distance is greater than or equal to
![]() $3$
, then we can consider the shortest path between these components and orient the edges along this path according to
$3$
, then we can consider the shortest path between these components and orient the edges along this path according to
![]() $\rho$
. The first and last oriented edges are pointing in opposite directions (each towards one of the connected components). So there exists a vertex in the middle of the path that is a fork for
$\rho$
. The first and last oriented edges are pointing in opposite directions (each towards one of the connected components). So there exists a vertex in the middle of the path that is a fork for
![]() $\rho$
. So there is a region with trace less than
$\rho$
. So there is a region with trace less than
![]() $C$
with a smaller distance to each connected component, which contradicts the minimality of the distance.
$C$
with a smaller distance to each connected component, which contradicts the minimality of the distance.
3.3 Escaping rays and neighbors
Let
![]() $P$
be a geodesic ray in the edge graph, starting at a vertex
$P$
be a geodesic ray in the edge graph, starting at a vertex
![]() $v_0$
and consisting of edges
$v_0$
and consisting of edges
![]() $e_n$
joining
$e_n$
joining
![]() $v_n$
to
$v_n$
to
![]() $v_{n+1}$
. Such a geodesic only passes once through each triangle of the edge graph. We say that such an infinite geodesic ray is an escaping ray if, for all
$v_{n+1}$
. Such a geodesic only passes once through each triangle of the edge graph. We say that such an infinite geodesic ray is an escaping ray if, for all
![]() $n \in \mathbb {N}$
, each edge
$n \in \mathbb {N}$
, each edge
![]() $e_n$
is directed from
$e_n$
is directed from
![]() $v_n$
to
$v_n$
to
![]() $v_{n+1}$
. Given a representation
$v_{n+1}$
. Given a representation
![]() $[\rho ] \in \mathfrak {X}_c$
, an infinite geodesic ray is called an escaping ray for
$[\rho ] \in \mathfrak {X}_c$
, an infinite geodesic ray is called an escaping ray for
![]() $\rho$
if it is an escaping ray with respect to the orientation induced by
$\rho$
if it is an escaping ray with respect to the orientation induced by
![]() $\rho$
, see Section 3.1.
$\rho$
, see Section 3.1.
We will prove that the existence of escaping rays for a given representation
![]() $\rho$
will imply that either the ray will eventually be contained in the boundary of a region
$\rho$
will imply that either the ray will eventually be contained in the boundary of a region
![]() $X \in \mathcal {C}^{(0)}$
such that
$X \in \mathcal {C}^{(0)}$
such that
![]() $\rho (X)$
only has eigenvalues on the unit circle (which is equivalent to
$\rho (X)$
only has eigenvalues on the unit circle (which is equivalent to
![]() $f(x) \leqslant 0$
according to Theorem2.7), or there are infinitely many regions with value bounded by a constant depending only on the boundary parameter
$f(x) \leqslant 0$
according to Theorem2.7), or there are infinitely many regions with value bounded by a constant depending only on the boundary parameter
![]() $c \in \mathbb {C}$
.
$c \in \mathbb {C}$
.
First we consider the case of an escaping ray that is included in the boundary of a given region in
![]() $\mathcal {C}^{(0)}$
, and then we will describe the general case.
$\mathcal {C}^{(0)}$
, and then we will describe the general case.
3.3.1 Neighbors around a region
In this subsection we are interested in the behavior of the values of the traces of regions that are all neighbors of a central one. Let
![]() $\alpha \in F_2$
. The neighbors of the region associated to
$\alpha \in F_2$
. The neighbors of the region associated to
![]() $\alpha$
are all associated to elements of the form
$\alpha$
are all associated to elements of the form
![]() $\gamma _n = \alpha ^n \beta$
for all
$\gamma _n = \alpha ^n \beta$
for all
![]() $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
.
Let
![]() $c \in \mathbb {C}$
and let
$c \in \mathbb {C}$
and let
![]() $[\rho ] \in \mathfrak {X}_c$
be a representation. Let
$[\rho ] \in \mathfrak {X}_c$
be a representation. Let
![]() $x = \mathrm {tr} (\rho (\alpha ))$
and consider the sequence defined by
$x = \mathrm {tr} (\rho (\alpha ))$
and consider the sequence defined by
![]() $u_n = \mathrm {tr} (\rho (\gamma _n))$
for all
$u_n = \mathrm {tr} (\rho (\gamma _n))$
for all
![]() $n \in \mathbb {Z}$
. The trace identity gives the following relation:
$n \in \mathbb {Z}$
. The trace identity gives the following relation:
To study the solutions of this recurrence relation we define
 $X_n = \left(\begin{matrix} u_{n+2} \\ u_{n+1} \\ u_n \end{matrix}\right) \in \mathbb {C}^3$
and consider the matrix
$X_n = \left(\begin{matrix} u_{n+2} \\ u_{n+1} \\ u_n \end{matrix}\right) \in \mathbb {C}^3$
and consider the matrix
 $M_x = \left(\begin{matrix} x & - \overline x & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{matrix}\right)$
, so that we have
$M_x = \left(\begin{matrix} x & - \overline x & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{matrix}\right)$
, so that we have
![]() $X_{n+1} = M_x X_n$
. The matrix
$X_{n+1} = M_x X_n$
. The matrix
![]() $M_x$
is conjugate to a matrix in
$M_x$
is conjugate to a matrix in
![]() $\textrm {SU} (2,1)$
and its characteristic polynomial is given by
$\textrm {SU} (2,1)$
and its characteristic polynomial is given by
![]() $\chi _x(s) = s^3 - x s^2 + \overline x s - 1$
. We can use Corollary2.7 to determine the behavior of the eigenvalues of
$\chi _x(s) = s^3 - x s^2 + \overline x s - 1$
. We can use Corollary2.7 to determine the behavior of the eigenvalues of
![]() $M_x$
, using the function
$M_x$
, using the function
![]() $f$
defined by
$f$
defined by
![]() $f(x) = \mathrm {Res} (\chi _x, \chi _x')$
, and hence of the sequence
$f(x) = \mathrm {Res} (\chi _x, \chi _x')$
, and hence of the sequence
![]() $(u_n)_{n\in \mathbb {Z}}$
depending on the value of
$(u_n)_{n\in \mathbb {Z}}$
depending on the value of
![]() $f(x)$
.
$f(x)$
.
If
![]() $f(x)=0$
, then the coefficients of the matrix
$f(x)=0$
, then the coefficients of the matrix
![]() $M_x^n$
grow at most quadratically in
$M_x^n$
grow at most quadratically in
![]() $n$
, and hence the growth of the sequence
$n$
, and hence the growth of the sequence
![]() $(X_n)_{n\in \mathbb {Z}}$
, and subsequently of the sequence
$(X_n)_{n\in \mathbb {Z}}$
, and subsequently of the sequence
![]() $(u_n)_{n\in \mathbb {Z}}$
, is at most quadratic, see Appendix A.1.
$(u_n)_{n\in \mathbb {Z}}$
, is at most quadratic, see Appendix A.1.
When
![]() $f(x) \neq 0$
, we can diagonalize the matrix
$f(x) \neq 0$
, we can diagonalize the matrix
![]() $M_x$
as
$M_x$
as
![]() $M_x = P D P^{-1}$
with
$M_x = P D P^{-1}$
with
 \begin{equation*}P = \left(\begin{matrix} \lambda & \frac {\bar \lambda }{\lambda } & \frac {\, 1\, }{\bar \lambda } \\ 1 & 1 & 1 \\ \frac {1}{\lambda } & \frac {\, \lambda \,}{\bar \lambda } & \bar \lambda \end{matrix}\right), \quad D = \left(\begin{matrix} \lambda & 0 & 0 \\ 0 & \frac {\bar \lambda }{\lambda } & 0 \\ 0 & 0 & \frac {\, 1\, }{\bar \lambda }\end{matrix}\right) \;\; \text { and } \;\; x = \lambda + \frac {\bar \lambda }{\lambda } + \frac {\, 1\, }{\bar \lambda }.\end{equation*}
\begin{equation*}P = \left(\begin{matrix} \lambda & \frac {\bar \lambda }{\lambda } & \frac {\, 1\, }{\bar \lambda } \\ 1 & 1 & 1 \\ \frac {1}{\lambda } & \frac {\, \lambda \,}{\bar \lambda } & \bar \lambda \end{matrix}\right), \quad D = \left(\begin{matrix} \lambda & 0 & 0 \\ 0 & \frac {\bar \lambda }{\lambda } & 0 \\ 0 & 0 & \frac {\, 1\, }{\bar \lambda }\end{matrix}\right) \;\; \text { and } \;\; x = \lambda + \frac {\bar \lambda }{\lambda } + \frac {\, 1\, }{\bar \lambda }.\end{equation*}
Hence we get
![]() $X_n = P D^n P^{-1} X_0,$
where
$X_n = P D^n P^{-1} X_0,$
where
 $X_0 = \left(\begin{matrix} u_2 \\ u_1 \\ u_0 \end{matrix}\right)$
.
$X_0 = \left(\begin{matrix} u_2 \\ u_1 \\ u_0 \end{matrix}\right)$
.
Let
![]() $(e_1, e_2, e_3)$
be the basis of
$(e_1, e_2, e_3)$
be the basis of
![]() $\mathbb {C}^3$
formed by the columns of the matrix
$\mathbb {C}^3$
formed by the columns of the matrix
![]() $P$
, which correspond to the eigenvectors of the matrix
$P$
, which correspond to the eigenvectors of the matrix
![]() $M_x$
. We can decompose
$M_x$
. We can decompose
![]() $X_0 = m_1 e_1 + m_2 e_2 + m_3 e_3$
with
$X_0 = m_1 e_1 + m_2 e_2 + m_3 e_3$
with
![]() $(m_1, m_2, m_3) \in \mathbb {C}^3$
. In that case, we get that
$(m_1, m_2, m_3) \in \mathbb {C}^3$
. In that case, we get that
If
![]() $f(x)\lt 0$
, then
$f(x)\lt 0$
, then
![]() $|\lambda | = 1$
and we see that the sequence
$|\lambda | = 1$
and we see that the sequence
![]() $(X_n)_{n\in \mathbb {Z}}$
stays bounded in
$(X_n)_{n\in \mathbb {Z}}$
stays bounded in
![]() $\mathbb {C}^3$
, and subsequently the sequence
$\mathbb {C}^3$
, and subsequently the sequence
![]() $(u_n)_{n\in \mathbb {Z}}$
is bounded as the projection of
$(u_n)_{n\in \mathbb {Z}}$
is bounded as the projection of
![]() $X_n$
on
$X_n$
on
![]() $\mathbb {C} \cdot e_3$
.
$\mathbb {C} \cdot e_3$
.
When
![]() $f(x) \gt 0$
, then we have
$f(x) \gt 0$
, then we have
![]() $|\lambda | \gt 1$
. If
$|\lambda | \gt 1$
. If
![]() $m_1 m_3 \neq 0$
we see that the sequence
$m_1 m_3 \neq 0$
we see that the sequence
![]() $X_n$
grows exponentially in both directions. However, it is possible to have
$X_n$
grows exponentially in both directions. However, it is possible to have
![]() $m_1 m_3=0$
and in that case the sequence will stay bounded in one direction. The purpose of the next lemma is to prove that the bound on such a sequence will only depend on the boundary parameter
$m_1 m_3=0$
and in that case the sequence will stay bounded in one direction. The purpose of the next lemma is to prove that the bound on such a sequence will only depend on the boundary parameter
![]() $c$
.
$c$
.
Lemma 3.8.
There exists a constant
![]() $D = D(c)$
, such that if the sequence
$D = D(c)$
, such that if the sequence
![]() $(u_n)_{n\in \mathbb {N}}$
defined above with
$(u_n)_{n\in \mathbb {N}}$
defined above with
![]() $f(x) \gt 0$
does not grow exponentially in both directions, then there are infinitely many terms of the sequence such that
$f(x) \gt 0$
does not grow exponentially in both directions, then there are infinitely many terms of the sequence such that
![]() $|u_n| \lt D$
.
$|u_n| \lt D$
.
Proof.
With the notation above, we are necessarily in the case
![]() $m_1 m_3=0$
. We can assume, without loss of generality, that
$m_1 m_3=0$
. We can assume, without loss of generality, that
![]() $m_1=0$
, so that we have
$m_1=0$
, so that we have
Since
![]() $|\lambda | \gt 1$
, we see that the sequence
$|\lambda | \gt 1$
, we see that the sequence
![]() $X_n$
will accumulate on a circle of radius
$X_n$
will accumulate on a circle of radius
![]() $|m_2 |$
in the complex line
$|m_2 |$
in the complex line
![]() $e_2$
. More precisely, for all
$e_2$
. More precisely, for all
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $n_0 \in \mathbb {N}$
, such that, for all
$n_0 \in \mathbb {N}$
, such that, for all
![]() $n \geqslant n_0$
, there exists
$n \geqslant n_0$
, there exists
![]() $\theta _n \in \mathbb {R}$
such that
$\theta _n \in \mathbb {R}$
such that
![]() $\Vert X_n - |m_2| e^{i\theta _n} e_2 \Vert \lt \varepsilon$
. In other words, for
$\Vert X_n - |m_2| e^{i\theta _n} e_2 \Vert \lt \varepsilon$
. In other words, for
![]() $n$
large enough, the vector
$n$
large enough, the vector
![]() $X_n$
gets arbitrarily close to the set
$X_n$
gets arbitrarily close to the set
![]() $\{ |m_2| e^{i\theta } e_2, \theta \in \mathbb {R} \}$
.
$\{ |m_2| e^{i\theta } e_2, \theta \in \mathbb {R} \}$
.
Hence, to prove the lemma, it suffices to find a uniform bound on
![]() $|m_2|$
that only depends on the boundary parameter
$|m_2|$
that only depends on the boundary parameter
![]() $c$
. Let
$c$
. Let
![]() $\varepsilon$
be arbitrarily small, and
$\varepsilon$
be arbitrarily small, and
![]() $n \geqslant n_0$
as above.
$n \geqslant n_0$
as above.
By definition of the sequence, we have
By denoting
![]() $\beta ' = \alpha ^{n+1} \beta$
we can write these values as
$\beta ' = \alpha ^{n+1} \beta$
we can write these values as
so we can identify the quadruple
![]() $(x, u_{n+1}, u_{n+2}, \overline {u_n})$
as the character of a representation in
$(x, u_{n+1}, u_{n+2}, \overline {u_n})$
as the character of a representation in
![]() $\mathfrak {X}_c$
. This means that the quadruple
$\mathfrak {X}_c$
. This means that the quadruple
![]() $(x, u_{n+1}, u_{n+2}, \overline {u_n})$
will satisfy the equations for
$(x, u_{n+1}, u_{n+2}, \overline {u_n})$
will satisfy the equations for
![]() $P$
and
$P$
and
![]() $Q$
with
$Q$
with
![]() $y=u_{n+1}, z=u_{n+2}$
and
$y=u_{n+1}, z=u_{n+2}$
and
![]() $t = \overline {u_n}$
.
$t = \overline {u_n}$
.
Using our hypothesis on
![]() $n$
, this quadruple is arbitrarily close to a quadruple of the form
$n$
, this quadruple is arbitrarily close to a quadruple of the form
![]() $\left (x, |m_2| e^{i \theta }, |m_2[ e^{i\theta } \frac {\bar \lambda }{\lambda }, |m_2| e^{-i\theta } \frac {\bar \lambda }{\lambda } \right ),$
for some
$\left (x, |m_2| e^{i \theta }, |m_2[ e^{i\theta } \frac {\bar \lambda }{\lambda }, |m_2| e^{-i\theta } \frac {\bar \lambda }{\lambda } \right ),$
for some
![]() $\theta \in \mathbb {R}.$
$\theta \in \mathbb {R}.$
By continuity of the expression relating
![]() $P$
and
$P$
and
![]() $Q$
with the quadruple of trace coordinates, we know that this ‘limit’ quadruple also satisfies the equations for
$Q$
with the quadruple of trace coordinates, we know that this ‘limit’ quadruple also satisfies the equations for
![]() $P$
and
$P$
and
![]() $Q$
and corresponds to an equivalence class of a representation in
$Q$
and corresponds to an equivalence class of a representation in
![]() $\mathfrak {X}_c$
.
$\mathfrak {X}_c$
.
We can first write the equation for
![]() $P$
with the quadruple
$P$
with the quadruple
![]() $\left (x, |m_2| e^{i \theta }, |m_2[ e^{i\theta } \frac {\bar \lambda }{\lambda }, |m_2| e^{-i\theta } \frac {\bar \lambda }{\lambda } \right )$
, which gives
$\left (x, |m_2| e^{i \theta }, |m_2[ e^{i\theta } \frac {\bar \lambda }{\lambda }, |m_2| e^{-i\theta } \frac {\bar \lambda }{\lambda } \right )$
, which gives
 \begin{align*} P & = |x|^2 |m_2|^2 + |x|^2+3 |m_2|^2 - 2 \Re \left (x |m_2| e^{i\theta } \displaystyle \frac {\, \lambda \,}{\bar \lambda } |m_2|e^{-i\theta } \right ) - 2 \Re \left ( \overline {x} |m_2|e^{i\theta } \frac {\, \bar \lambda \, }{\lambda } |m_2|e^{-i\theta } \right ) -3 \\ & = |m_2|^2 \left ( |x|^2 - 4 \Re \left ( x \frac {\lambda }{\, \bar \lambda \, } \right ) +3\right ) - 3 + |x|^2. \end{align*}
\begin{align*} P & = |x|^2 |m_2|^2 + |x|^2+3 |m_2|^2 - 2 \Re \left (x |m_2| e^{i\theta } \displaystyle \frac {\, \lambda \,}{\bar \lambda } |m_2|e^{-i\theta } \right ) - 2 \Re \left ( \overline {x} |m_2|e^{i\theta } \frac {\, \bar \lambda \, }{\lambda } |m_2|e^{-i\theta } \right ) -3 \\ & = |m_2|^2 \left ( |x|^2 - 4 \Re \left ( x \frac {\lambda }{\, \bar \lambda \, } \right ) +3\right ) - 3 + |x|^2. \end{align*}
So we obtain an expression for
![]() $|m_2|$
in terms of
$|m_2|$
in terms of
![]() $P$
and
$P$
and
![]() $x$
:
$x$
:
 \begin{equation} |m_2|^2 = \dfrac {P+3 - |x|^2}{|x|^2 - 4 \Re \left ( x \frac {\, \lambda \, }{\bar \lambda } \right ) +3}. \end{equation}
\begin{equation} |m_2|^2 = \dfrac {P+3 - |x|^2}{|x|^2 - 4 \Re \left ( x \frac {\, \lambda \, }{\bar \lambda } \right ) +3}. \end{equation}
The equation for
![]() $Q$
gives
$Q$
gives
 \begin{align*} & Q = |m_2|^4 \left (5 + |x|^2+2 \Re \left ( 2 \left (\frac {\bar \lambda }{\lambda }\right )^3- 2 \overline x \frac {\bar \lambda }{\lambda } - x \left (\frac {\bar \lambda }{\lambda }\right )^2 \right ) \right ) \\ & + |m_2|^2 \left ( |x|^4+3|x|^2-18+2\Re \left ( 2 x^2 \frac {\bar \lambda }{\lambda }-3 x \left (\frac {\bar \lambda }{\lambda }\right )^2+6 \overline x \frac {\bar \lambda }{\lambda } - 2 |x|^2 \overline x \frac {\bar \lambda }{\lambda }+\overline x^2 \left ( \frac {\bar \lambda }{\lambda }\right )^2-x^3 \right ) \right ) \\ & + 9 - 6|x|^2+2\Re (x^3). \end{align*}
\begin{align*} & Q = |m_2|^4 \left (5 + |x|^2+2 \Re \left ( 2 \left (\frac {\bar \lambda }{\lambda }\right )^3- 2 \overline x \frac {\bar \lambda }{\lambda } - x \left (\frac {\bar \lambda }{\lambda }\right )^2 \right ) \right ) \\ & + |m_2|^2 \left ( |x|^4+3|x|^2-18+2\Re \left ( 2 x^2 \frac {\bar \lambda }{\lambda }-3 x \left (\frac {\bar \lambda }{\lambda }\right )^2+6 \overline x \frac {\bar \lambda }{\lambda } - 2 |x|^2 \overline x \frac {\bar \lambda }{\lambda }+\overline x^2 \left ( \frac {\bar \lambda }{\lambda }\right )^2-x^3 \right ) \right ) \\ & + 9 - 6|x|^2+2\Re (x^3). \end{align*}
Using the expression of
![]() $|m_2|^2$
found above and replacing
$|m_2|^2$
found above and replacing
![]() $x = \lambda + \frac {\bar \lambda }{\lambda } + \frac {1}{\bar \lambda }$
and writing
$x = \lambda + \frac {\bar \lambda }{\lambda } + \frac {1}{\bar \lambda }$
and writing
![]() $\lambda = r e^{is}$
with
$\lambda = r e^{is}$
with
![]() $r \gt 0$
and
$r \gt 0$
and
![]() $s \in \mathbb {R}$
, we can obtain (for example, using Mathematica) the following formula:
$s \in \mathbb {R}$
, we can obtain (for example, using Mathematica) the following formula:
This means that
![]() $r$
is one of the finitely many solutions of the equation above. At this point, we have already proved that if the sequence
$r$
is one of the finitely many solutions of the equation above. At this point, we have already proved that if the sequence
![]() $(u_n)_{n\in \mathbb {N}}$
does not grow exponentially, then
$(u_n)_{n\in \mathbb {N}}$
does not grow exponentially, then
![]() $|\lambda |$
and hence
$|\lambda |$
and hence
![]() $|x|$
can only take finitely many values that only depend on
$|x|$
can only take finitely many values that only depend on
![]() $P$
and
$P$
and
![]() $Q$
. Moreover, we cannot have
$Q$
. Moreover, we cannot have
![]() $r=1$
as a solution as in that case we would have
$r=1$
as a solution as in that case we would have
![]() $f(x)=0$
which is excluded from our consideration.
$f(x)=0$
which is excluded from our consideration.
Finally, if we look at (4) we see that its denominator can be written as
which makes it clear that the denominator of the expression can only be equal to
![]() $0$
when
$0$
when
![]() $\lambda \in \zeta _3$
and hence when
$\lambda \in \zeta _3$
and hence when
![]() $|\lambda | = 1$
. This means that if
$|\lambda | = 1$
. This means that if
![]() $r = |\lambda |$
is one of the finitely many solutions of (5), then the expression of
$r = |\lambda |$
is one of the finitely many solutions of (5), then the expression of
![]() $|m_2|^2$
is bounded by a value that depends only on
$|m_2|^2$
is bounded by a value that depends only on
![]() $P$
and
$P$
and
![]() $Q$
, and hence that depends only on
$Q$
, and hence that depends only on
![]() $c$
.
$c$
.
We can conclude that there exists
![]() $D = D(c)$
, only depending on
$D = D(c)$
, only depending on
![]() $c$
, such that
$c$
, such that
![]() $|m_2| \lt D$
. Thus, if the sequence
$|m_2| \lt D$
. Thus, if the sequence
![]() $(u_n)_{n\in \mathbb {Z}}$
does not grow exponentially for
$(u_n)_{n\in \mathbb {Z}}$
does not grow exponentially for
![]() $n \longrightarrow + \infty$
, then
$n \longrightarrow + \infty$
, then
![]() $|u_n|$
will converge to a value smaller than
$|u_n|$
will converge to a value smaller than
![]() $D$
.
$D$
.
Remark 3.9. We can use the previous proof to produce an algorithm to find the constant
![]() $D$
. Precisely, first solve for
$D$
. Precisely, first solve for
![]() $r^2$
using (5) and then plug it into (4) to obtain a formula for
$r^2$
using (5) and then plug it into (4) to obtain a formula for
![]() $|m_2|$
in terms of
$|m_2|$
in terms of
![]() $P,Q$
and
$P,Q$
and
![]() $s$
. A value for
$s$
. A value for
![]() $D$
can be taken to be
$D$
can be taken to be
![]() $|m_2|+\epsilon$
. So we need to find the maximum of
$|m_2|+\epsilon$
. So we need to find the maximum of
![]() $|m_2|$
on the circle (parametrized by
$|m_2|$
on the circle (parametrized by
![]() $s$
), which can always be done numerically.
$s$
), which can always be done numerically.
For the rest of the paper, for all
![]() $c \in \mathbb {C}$
, we set
$c \in \mathbb {C}$
, we set
Lemma3.8 implies the following result.
Lemma 3.10.
Let
![]() $c \in \mathbb {C}$
. There exists a function
$c \in \mathbb {C}$
. There exists a function
![]() $H_c \colon \thinspace \mathbb {C} \rightarrow \mathbb {R} \cup \{ \infty \}$
with the following properties, for all
$H_c \colon \thinspace \mathbb {C} \rightarrow \mathbb {R} \cup \{ \infty \}$
with the following properties, for all
![]() $x \in \mathbb {C}$
:
$x \in \mathbb {C}$
:
-
(a)
 $H_c(x) = H_c(\overline x)$
;
$H_c(x) = H_c(\overline x)$
; -
(b)
 $H_c(x) \geqslant M(c)$
;
$H_c(x) \geqslant M(c)$
; -
(c)
 $H_c(x) = \infty$
if and only if
$H_c(x) = \infty$
if and only if
 $f(x)\leqslant 0$
;
$f(x)\leqslant 0$
; -
(d) if
 $f(x) \gt 0$
, then for any sequence
$f(x) \gt 0$
, then for any sequence
 $u_n$
as above satisfying
(3)
and coming from a representation
$u_n$
as above satisfying
(3)
and coming from a representation
 $[\rho ] \in \mathfrak {X}_c$
, there exists
$[\rho ] \in \mathfrak {X}_c$
, there exists
 $n_1, n_2 \in \mathbb {Z} \cup \{ \pm \infty \}$
such that:
$n_1, n_2 \in \mathbb {Z} \cup \{ \pm \infty \}$
such that:
-
(i)
 $|u_n| \leqslant H_c(x)$
if and only if
$|u_n| \leqslant H_c(x)$
if and only if
 $n_1 \leqslant n \leqslant n_2$
;
$n_1 \leqslant n \leqslant n_2$
; -
(ii)
 $|u_n|$
is monotonically decreasing for
$|u_n|$
is monotonically decreasing for
 $n \lt n_1$
and increasing for
$n \lt n_1$
and increasing for
 $n \gt n_2$
.
$n \gt n_2$
.
-
There are similar statements in previous works ([Reference BowditchBow98 3.14], [Reference Tan, Wong and ZhangTWZ08, 3.20], [Reference Maloni, Palesi and TanMPT15, 4.15] and [Reference Maloni and PalesiMP20, 3.4.1]) that all rely on the same basic principle. We refer the interested reader to the proofs given in these papers that are in simpler cases.
Proof. We will omit certain computational details for clarity.
First, we simply set
![]() $H_c (x) = \infty$
when
$H_c (x) = \infty$
when
![]() $f(x) \leqslant 0$
.
$f(x) \leqslant 0$
.
Now, let
![]() $x \in \mathbb {C}$
, such that
$x \in \mathbb {C}$
, such that
![]() $f(x) \gt 0$
. Assume that we have
$f(x) \gt 0$
. Assume that we have
![]() $[\rho ] \in \mathfrak {X}_c$
, a region
$[\rho ] \in \mathfrak {X}_c$
, a region
![]() $X \in \Omega$
such that
$X \in \Omega$
such that
![]() $x = \mathrm {tr} (\rho (X))$
and the sequence
$x = \mathrm {tr} (\rho (X))$
and the sequence
![]() $(u_n)$
defined as before. So
$(u_n)$
defined as before. So
![]() $(u_n)$
satisfies (3) and is such that
$(u_n)$
satisfies (3) and is such that
![]() $(x, u_1, u_2, \overline {u_0} )$
is the character of the representation
$(x, u_1, u_2, \overline {u_0} )$
is the character of the representation
![]() $\rho$
. As discussed above, there exists
$\rho$
. As discussed above, there exists
![]() $(m_1, m_2, m_3) \in \mathbb {C}^3$
such that
$(m_1, m_2, m_3) \in \mathbb {C}^3$
such that
Assume first that
![]() $m_1 m_3 \neq 0$
. Up to reindexing the sequence we can assume that
$m_1 m_3 \neq 0$
. Up to reindexing the sequence we can assume that
![]() $|m_3| \leqslant |m_1| \leqslant |\lambda |^2 |m_3|$
. The quadruple
$|m_3| \leqslant |m_1| \leqslant |\lambda |^2 |m_3|$
. The quadruple
![]() $(x,u_1, u_2, \overline {u_0} )$
satisfies the equations for
$(x,u_1, u_2, \overline {u_0} )$
satisfies the equations for
![]() $P$
and
$P$
and
![]() $Q$
, so using an argument similar to the one for finding the bound on
$Q$
, so using an argument similar to the one for finding the bound on
![]() $|m_2|$
in the proof of Lemma3.8, we can show that there exists a constant
$|m_2|$
in the proof of Lemma3.8, we can show that there exists a constant
![]() $K_c (x)$
such that
$K_c (x)$
such that
![]() $\frac {|m_2|}{\sqrt {|m_1m_3|}}$
and
$\frac {|m_2|}{\sqrt {|m_1m_3|}}$
and
![]() $|m_1 m_3|$
are both less than
$|m_1 m_3|$
are both less than
![]() $K_c (x)$
. One can see that
$K_c (x)$
. One can see that
 \begin{align*} \frac {|u_{n+2}| - |u_{n+1}|}{\sqrt {|m_1 m_3|}} & \geqslant |\lambda |^n \sqrt {\frac {|m_1|}{|m_3|} } ( |\lambda | - 1) - 2 \frac {m_2}{\sqrt {|m_1 m_3|}} - \sqrt {\frac {|m_3|}{|m_1|}} \frac {1}{|\lambda |^{n+1}} (|\lambda |+1) \\[5pt] & \geqslant |\lambda |^n (|\lambda |-1) - 2 K_c(x) - (|\lambda |+1). \end{align*}
\begin{align*} \frac {|u_{n+2}| - |u_{n+1}|}{\sqrt {|m_1 m_3|}} & \geqslant |\lambda |^n \sqrt {\frac {|m_1|}{|m_3|} } ( |\lambda | - 1) - 2 \frac {m_2}{\sqrt {|m_1 m_3|}} - \sqrt {\frac {|m_3|}{|m_1|}} \frac {1}{|\lambda |^{n+1}} (|\lambda |+1) \\[5pt] & \geqslant |\lambda |^n (|\lambda |-1) - 2 K_c(x) - (|\lambda |+1). \end{align*}
Hence, if
![]() $|\lambda |^n$
is larger than some constant
$|\lambda |^n$
is larger than some constant
![]() $L_c (x):= \frac {2K_c (x) + (|\lambda | + 1)}{|\lambda |-1}$
, then we have that
$L_c (x):= \frac {2K_c (x) + (|\lambda | + 1)}{|\lambda |-1}$
, then we have that
![]() $|u_{n+2}| \geqslant |u_{n+1}|$
.
$|u_{n+2}| \geqslant |u_{n+1}|$
.
On the other hand, as
![]() $|u_{n+1}| \leqslant |m_1| |\lambda |^n + |m_2| + |m_3| \frac {1}{|\lambda |^n}$
, we infer that there exists
$|u_{n+1}| \leqslant |m_1| |\lambda |^n + |m_2| + |m_3| \frac {1}{|\lambda |^n}$
, we infer that there exists
![]() $H_c(x)$
such that if
$H_c(x)$
such that if
![]() $|u_{n+1}| \geqslant H_c (x)$
, then
$|u_{n+1}| \geqslant H_c (x)$
, then
![]() $|\lambda |^n \geqslant L_c (x)$
. Hence, for indices such that
$|\lambda |^n \geqslant L_c (x)$
. Hence, for indices such that
![]() $|u_n| \geqslant H_c (x)$
we have that the sequence is monotonically increasing, which is the desired condition.
$|u_n| \geqslant H_c (x)$
we have that the sequence is monotonically increasing, which is the desired condition.
We can choose
![]() $H_c (x)$
to be always bigger than
$H_c (x)$
to be always bigger than
![]() $M(c)$
so thatm in the case
$M(c)$
so thatm in the case
![]() $m_1 m_3=0$
, Lemma3.8 gives the desired result. The sequence
$m_1 m_3=0$
, Lemma3.8 gives the desired result. The sequence
![]() $u_{-n}$
behaves in a similar way, simply replacing
$u_{-n}$
behaves in a similar way, simply replacing
![]() $x$
with
$x$
with
![]() $\bar x$
, and hence this shows that
$\bar x$
, and hence this shows that
![]() $H_c( x) = H_c (\bar x)$
.
$H_c( x) = H_c (\bar x)$
.
3.3.2 Escaping rays
Using the constant
![]() $M(c)$
defined in (6) we now prove the following.
$M(c)$
defined in (6) we now prove the following.
Lemma 3.11.
Let
![]() $c \in \mathbb {C}$
and
$c \in \mathbb {C}$
and
![]() $[\rho ] \in \mathfrak {X}_c$
. Set
$[\rho ] \in \mathfrak {X}_c$
. Set
![]() $M(c):=\max \{6, \sqrt {|\Re (c)|}, D(c)\}$
. Suppose that
$M(c):=\max \{6, \sqrt {|\Re (c)|}, D(c)\}$
. Suppose that
![]() $\{ e_n \}_{n\in \mathbb {N}}$
is an escaping ray. Then there are two cases:
$\{ e_n \}_{n\in \mathbb {N}}$
is an escaping ray. Then there are two cases:
-
(i) there exists region
 $\alpha$
such that the ray is eventually contained in the boundary of
$\alpha$
such that the ray is eventually contained in the boundary of
 $\alpha$
, such that
$\alpha$
, such that
 $f (x ) \leqslant 0$
with
$f (x ) \leqslant 0$
with
 $x = \mathrm {tr} (\rho (\alpha ))$
; or
$x = \mathrm {tr} (\rho (\alpha ))$
; or
-
(ii) the ray meets infinitely many distinct regions with trace smaller than
 $M(c)$
.
$M(c)$
.
Proof.
Let
![]() $(e_i)_{i\in \mathbb {N}}$
be an escaping ray. First, assume that the ray is eventually contained in the neighborhood of some region
$(e_i)_{i\in \mathbb {N}}$
be an escaping ray. First, assume that the ray is eventually contained in the neighborhood of some region
![]() $\alpha$
, and note
$\alpha$
, and note
![]() $x = \mathrm {tr} (\rho (\alpha ))$
. If
$x = \mathrm {tr} (\rho (\alpha ))$
. If
![]() $f(x) \leqslant 0$
, then we are in the first case. Otherwise, we have
$f(x) \leqslant 0$
, then we are in the first case. Otherwise, we have
![]() $f(x) \gt 0$
. Note that the sequence
$f(x) \gt 0$
. Note that the sequence
![]() $(|u_n|)_{n\in \mathbb {N}}$
of traces of regions around
$(|u_n|)_{n\in \mathbb {N}}$
of traces of regions around
![]() $x$
cannot be exponentially growing with respect to
$x$
cannot be exponentially growing with respect to
![]() $n$
, or else the ray would not be escaping. From the previous lemma, it means that there are infinitely many distinct regions with trace smaller than
$n$
, or else the ray would not be escaping. From the previous lemma, it means that there are infinitely many distinct regions with trace smaller than
![]() $D (c)$
.
$D (c)$
.
Now assume that the escaping ray
![]() $(e_i)_{i \in \mathbb {N}}$
does not eventually end in the neighborhood of a given region. We consider a
$(e_i)_{i \in \mathbb {N}}$
does not eventually end in the neighborhood of a given region. We consider a
![]() $4$
-coloring of the complex
$4$
-coloring of the complex
![]() $\mathcal {E}$
as described in Section 2.2. Let
$\mathcal {E}$
as described in Section 2.2. Let
![]() $(X_i)_{i\in \mathbb {N}}, (Y_i)_{i\in \mathbb {N}}, (Z_i)_{i\in \mathbb {N}}, (T_i)_{i\in \mathbb {N}}$
be the four sequences of regions corresponding to the four regions around the head of edge
$(X_i)_{i\in \mathbb {N}}, (Y_i)_{i\in \mathbb {N}}, (Z_i)_{i\in \mathbb {N}}, (T_i)_{i\in \mathbb {N}}$
be the four sequences of regions corresponding to the four regions around the head of edge
![]() $e_i$
, with the letters
$e_i$
, with the letters
![]() $X,Y,Z,T$
each corresponding to a given color. Let
$X,Y,Z,T$
each corresponding to a given color. Let
![]() $x_i = \mathrm {tr} (\rho (X_i))$
; and similarly for
$x_i = \mathrm {tr} (\rho (X_i))$
; and similarly for
![]() $y_i, z_i, t_i$
.
$y_i, z_i, t_i$
.
As the escaping ray does not end in the neighbors of a given region, we see that the four sequences
![]() $|x_i|, |y_i|, |z_i|, |t_i|$
are infinite, decreasing and bounded below. So the modulus of each sequence is converging towards some limit.
$|x_i|, |y_i|, |z_i|, |t_i|$
are infinite, decreasing and bounded below. So the modulus of each sequence is converging towards some limit.
For all
![]() $\epsilon \gt 0$
, there exists
$\epsilon \gt 0$
, there exists
![]() $n_0$
such that, for all
$n_0$
such that, for all
![]() $n \geqslant n_0$
, the vertex
$n \geqslant n_0$
, the vertex
![]() $v_n$
between the two consecutive directed edges
$v_n$
between the two consecutive directed edges
![]() $e_n$
and
$e_n$
and
![]() $e_{n+1}$
is an
$e_{n+1}$
is an
![]() $\epsilon$
-fork. For
$\epsilon$
-fork. For
![]() $\epsilon$
small enough, we can then apply the
$\epsilon$
small enough, we can then apply the
![]() $\epsilon$
-fork lemma to conclude that for all
$\epsilon$
-fork lemma to conclude that for all
![]() $n \geqslant n_0$
there is at least one region around the vertex
$n \geqslant n_0$
there is at least one region around the vertex
![]() $v_{n}$
that has trace smaller than
$v_{n}$
that has trace smaller than
![]() $C:= \max \{6, \sqrt {|\Re (c)|} \}$
. As the escaping ray is not contained in the neighborhood of a given region, we know that there will be infinitely many distinct such regions.
$C:= \max \{6, \sqrt {|\Re (c)|} \}$
. As the escaping ray is not contained in the neighborhood of a given region, we know that there will be infinitely many distinct such regions.
3.4 Bowditch representations
We can now define Bowditch representations.
Definition 3.12. Let
![]() $c \in \mathbb {C}$
, and let
$c \in \mathbb {C}$
, and let
![]() $\rho \colon \thinspace F_2 \rightarrow \mathrm {SU}(2,1)$
be a representation such that
$\rho \colon \thinspace F_2 \rightarrow \mathrm {SU}(2,1)$
be a representation such that
![]() $[\rho ]\in \mathfrak {X}_c$
. We say that
$[\rho ]\in \mathfrak {X}_c$
. We say that
![]() $\rho$
is a Bowditch representation if:
$\rho$
is a Bowditch representation if:
-
(i)
 $\forall \gamma \in \mathcal {S}$
, we have that
$\forall \gamma \in \mathcal {S}$
, we have that
 $\rho (\gamma )$
is loxodromic and
$\rho (\gamma )$
is loxodromic and -
(ii) the set
 $\Omega (M) = \{ \gamma \in \mathcal {S} \ | \ \mathrm {tr} (\rho (\gamma )) \lt M \}$
is finite,
$\Omega (M) = \{ \gamma \in \mathcal {S} \ | \ \mathrm {tr} (\rho (\gamma )) \lt M \}$
is finite,
where
![]() $M = M(c)$
as defined in (6).
$M = M(c)$
as defined in (6).
We denote by
![]() $\mathfrak {X}_{BQ,c} = \mathfrak {X}_{BQ, c}(F_2, \mathrm {SU}(2, 1))$
the set of conjugacy classes of representation in
$\mathfrak {X}_{BQ,c} = \mathfrak {X}_{BQ, c}(F_2, \mathrm {SU}(2, 1))$
the set of conjugacy classes of representation in
![]() $\mathfrak {X}_c$
that are Bowditch and, more generally, we denote
$\mathfrak {X}_c$
that are Bowditch and, more generally, we denote
The following result is an immediate consequence of Lemmas3.8 and 3.11.
Lemma 3.13.
If
![]() $[\rho ] \in \mathfrak {X}_{BQ}$
, then there will be no escaping rays for
$[\rho ] \in \mathfrak {X}_{BQ}$
, then there will be no escaping rays for
![]() $\rho$
. Moreover, for any region
$\rho$
. Moreover, for any region
![]() $X \in \Omega$
and neighboring regions
$X \in \Omega$
and neighboring regions
![]() $\{Y_n\}$
around
$\{Y_n\}$
around
![]() $X$
, the absolute value of traces
$X$
, the absolute value of traces
![]() $|\mathrm {tr}\left (\rho (Y_n)\right )|$
will have exponential growth in both directions.
$|\mathrm {tr}\left (\rho (Y_n)\right )|$
will have exponential growth in both directions.
3.5 Attracting subgraph
3.5.1 Attracting arc
Recall that we have the following identifications:
![]() $\Omega = \mathcal {C}^{(0)} = \mathcal {S}$
. We will make use of Lemma3.10 to define an attracting subgraph in the neighborhood of certain regions.
$\Omega = \mathcal {C}^{(0)} = \mathcal {S}$
. We will make use of Lemma3.10 to define an attracting subgraph in the neighborhood of certain regions.
Let
![]() $c \in \mathbb {C}$
,
$c \in \mathbb {C}$
,
![]() $[\rho ] \in \mathfrak {X}_c$
and
$[\rho ] \in \mathfrak {X}_c$
and
![]() $K \geqslant M(c)$
. For each region
$K \geqslant M(c)$
. For each region
![]() $X \in \Omega (K)$
, we define
$X \in \Omega (K)$
, we define
This is a connected non-empty subarc in
![]() $\partial X$
with the following properties:
$\partial X$
with the following properties:
-
(i) every directed edge
 $\vec e_\rho$
such that
$\vec e_\rho$
such that
 $e \in \partial X$
that is not in
$e \in \partial X$
that is not in
 $J_\rho (K, X)$
points towards
$J_\rho (K, X)$
points towards
 $J_\rho (K, X)$
;
$J_\rho (K, X)$
; -
(ii) if
 $Y \in \Omega (K)$
and
$Y \in \Omega (K)$
and
 $e \in \partial X$
has one vertex
$e \in \partial X$
has one vertex
 $v = (X, Y) \in \mathcal {E}^{(0)}$
, then
$v = (X, Y) \in \mathcal {E}^{(0)}$
, then
 $e \in J_\rho (K, X)$
.
$e \in J_\rho (K, X)$
.
This definition is similar to the definitions used in Tan, Wong and Zhang [Reference Tan, Wong and ZhangTWZ08] and Maloni, Palesi and Tan [Reference Maloni, Palesi and TanMPT15]. However, in our setting, we need to define a subgraph that is slightly larger than this subarc, but with similar properties, because of the way we define a subtree to be ‘attracting’. Recall that the graph
![]() $\mathcal {E}$
is a ‘trivalent tree of triangles’ in the sense that it is a graph made of triangles, one for each triangle
$\mathcal {E}$
is a ‘trivalent tree of triangles’ in the sense that it is a graph made of triangles, one for each triangle
![]() $T$
in
$T$
in
![]() $\mathcal {C}^{(2)}$
. We want to define a bigger set
$\mathcal {C}^{(2)}$
. We want to define a bigger set
![]() $\widetilde {J}_\rho (K, X) \subset \mathcal {E}^{(1)}$
with the property that, if one edge
$\widetilde {J}_\rho (K, X) \subset \mathcal {E}^{(1)}$
with the property that, if one edge
![]() $e$
is in
$e$
is in
![]() $J_\rho (K, X)$
, we want to add, in
$J_\rho (K, X)$
, we want to add, in
![]() $\widetilde {J}_\rho (K, X)$
, the whole triangle that
$\widetilde {J}_\rho (K, X)$
, the whole triangle that
![]() $e$
is part of. It is clear that
$e$
is part of. It is clear that
![]() $J_\rho (K, X) \subset \widetilde {J}_\rho (K, X)$
. We say that a triangle
$J_\rho (K, X) \subset \widetilde {J}_\rho (K, X)$
. We say that a triangle
![]() $\Delta \subset \mathcal {E}^{(1)}$
is in the boundary
$\Delta \subset \mathcal {E}^{(1)}$
is in the boundary
![]() $\partial X$
of the region
$\partial X$
of the region
![]() $X$
if one of its edges has this property. So we define the set
$X$
if one of its edges has this property. So we define the set
![]() $\widetilde {J}_\rho (K, X)$
as a connected union of triangles in
$\widetilde {J}_\rho (K, X)$
as a connected union of triangles in
![]() $\partial X$
satisfying the following properties.
$\partial X$
satisfying the following properties.
-
(i) For each triangle
 $\Delta$
in
$\Delta$
in
 $\partial X$
such that
$\partial X$
such that
 $\Delta$
is not in
$\Delta$
is not in
 $\widetilde {J}_\rho (K,X)$
, then, for each vertex
$\widetilde {J}_\rho (K,X)$
, then, for each vertex
 $v$
of
$v$
of
 $\Delta$
, the directed edge from
$\Delta$
, the directed edge from
 $v$
forming a geodesic towards
$v$
forming a geodesic towards
 $\widetilde {J}_\rho (K, X)$
is pointing towards
$\widetilde {J}_\rho (K, X)$
is pointing towards
 $\widetilde {J}_\rho (K, X)$
.Footnote
1
$\widetilde {J}_\rho (K, X)$
.Footnote
1
-
(ii) If
 $Y \in \Omega (K)$
and
$Y \in \Omega (K)$
and
 $\Delta$
is a triangle adjacent to
$\Delta$
is a triangle adjacent to
 $X$
and
$X$
and
 $Y$
, then
$Y$
, then
 $\Delta$
is in
$\Delta$
is in
 $\widetilde {J}_\rho (K, X)$
.
$\widetilde {J}_\rho (K, X)$
.
We can now explain better why we need to define this extension. Let
![]() $e$
be an edge which is part of a ‘triangle’
$e$
be an edge which is part of a ‘triangle’
![]() $\Delta$
. It could happen that
$\Delta$
. It could happen that
![]() $e\in J_\rho (K, X)$
but no other edge of
$e\in J_\rho (K, X)$
but no other edge of
![]() $\Delta$
is. In this situation, the geodesics from the vertex of
$\Delta$
is. In this situation, the geodesics from the vertex of
![]() $\Delta \setminus e$
to
$\Delta \setminus e$
to
![]() $J_\rho (K, X)$
are not unique and it could happen that it is not true any longer that both those geodesic paths point towards
$J_\rho (K, X)$
are not unique and it could happen that it is not true any longer that both those geodesic paths point towards
![]() $J_\rho (K, X)$
, as we will require in the definition of
$J_\rho (K, X)$
, as we will require in the definition of
![]() $\rho$
-attracting below.
$\rho$
-attracting below.
3.5.2 Attracting subgraph
Definition 3.14. A non-empty subgraph
![]() $T \subset \mathcal {E}$
is said to be
$T \subset \mathcal {E}$
is said to be
![]() $\rho$
-attracting if, for every vertex
$\rho$
-attracting if, for every vertex
![]() $v\in \mathcal {E}^{(0)}$
such that
$v\in \mathcal {E}^{(0)}$
such that
![]() $v \notin T$
and for every geodesic in
$v \notin T$
and for every geodesic in
![]() $\mathcal {E}$
from
$\mathcal {E}$
from
![]() $v$
to
$v$
to
![]() $T$
, each
$T$
, each
![]() $\rho$
-oriented edge along the geodesic points towards
$\rho$
-oriented edge along the geodesic points towards
![]() $T$
.
$T$
.
For all
![]() $K \geqslant M(c)$
we constructed a subarc
$K \geqslant M(c)$
we constructed a subarc
![]() $\widetilde {J}_\rho (K, X)$
for all regions
$\widetilde {J}_\rho (K, X)$
for all regions
![]() $X \in \Omega = \mathcal {S}$
. We can now define the graph
$X \in \Omega = \mathcal {S}$
. We can now define the graph
This set is a subgraph of
![]() $\mathcal {E}$
and we can prove the following result.
$\mathcal {E}$
and we can prove the following result.
Proposition 3.15.
If
![]() $K \geqslant M(c)$
, then the subgraph
$K \geqslant M(c)$
, then the subgraph
![]() $T_\rho (K)$
is connected and
$T_\rho (K)$
is connected and
![]() $\rho$
-attracting.
$\rho$
-attracting.
Proof.
First, let us show that
![]() $\mathcal {T} = T_\rho (K)$
is connected. Let
$\mathcal {T} = T_\rho (K)$
is connected. Let
![]() $e, e'$
be two edges of
$e, e'$
be two edges of
![]() $\mathcal {T}$
. Then
$\mathcal {T}$
. Then
![]() $e$
and
$e$
and
![]() $e'$
belong to a triangle adjacent to regions
$e'$
belong to a triangle adjacent to regions
![]() $X, X' \in \Omega (K)$
. As
$X, X' \in \Omega (K)$
. As
![]() $\Omega (K)$
is connected, we can find a sequence of regions
$\Omega (K)$
is connected, we can find a sequence of regions
![]() $X = X_0, X_1, \dots, X_n = X'$
such that
$X = X_0, X_1, \dots, X_n = X'$
such that
![]() $X_k$
is adjacent to
$X_k$
is adjacent to
![]() $X_{k+1}$
for all
$X_{k+1}$
for all
![]() $k$
. Hence there are triangles
$k$
. Hence there are triangles
![]() $\Delta _0, \ldots, \Delta _n$
, such that each
$\Delta _0, \ldots, \Delta _n$
, such that each
![]() $\Delta _k$
is adjacent to both
$\Delta _k$
is adjacent to both
![]() $X_k$
and
$X_k$
and
![]() $X_{k+1}$
, and by construction this triangle is in
$X_{k+1}$
, and by construction this triangle is in
![]() $T_{\rho }(K)$
. Since the union of triangles in
$T_{\rho }(K)$
. Since the union of triangles in
![]() $\widetilde {J}_{\rho } (K, X_k)$
is connected, the triangles
$\widetilde {J}_{\rho } (K, X_k)$
is connected, the triangles
![]() $\Delta _k$
and
$\Delta _k$
and
![]() $\Delta _{k+1}$
are connected in
$\Delta _{k+1}$
are connected in
![]() $\widetilde {J}_{\rho } (K, X)$
, and hence the two edges
$\widetilde {J}_{\rho } (K, X)$
, and hence the two edges
![]() $e$
and
$e$
and
![]() $e'$
are connected by a path in
$e'$
are connected by a path in
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Second, let us show that
![]() $\mathcal {T} = T_\rho (K)$
is
$\mathcal {T} = T_\rho (K)$
is
![]() $\rho$
-attracting. Let
$\rho$
-attracting. Let
![]() $e = (X,Y,Z ; T, T')$
be an edge that intersects
$e = (X,Y,Z ; T, T')$
be an edge that intersects
![]() $\mathcal {T}$
at a vertex
$\mathcal {T}$
at a vertex
![]() $v = (X,Y) \in \mathcal {E}^{(0)}$
, but that is not in
$v = (X,Y) \in \mathcal {E}^{(0)}$
, but that is not in
![]() $\mathcal {T}$
(so
$\mathcal {T}$
(so
![]() $e$
is in the circular neighborhood of
$e$
is in the circular neighborhood of
![]() $\mathcal {T}$
). This means that the triangle
$\mathcal {T}$
). This means that the triangle
![]() $\Delta$
adjacent to
$\Delta$
adjacent to
![]() $X,Y,T$
is in
$X,Y,T$
is in
![]() $\mathcal {T}$
, but the triangle
$\mathcal {T}$
, but the triangle
![]() $\Delta '$
adjacent to
$\Delta '$
adjacent to
![]() $X,Y,Z$
is not.
$X,Y,Z$
is not.
By construction, one of the regions
![]() $X,Y,T$
is in
$X,Y,T$
is in
![]() $\Omega _\rho (K)$
. If
$\Omega _\rho (K)$
. If
![]() $X$
or
$X$
or
![]() $Y$
is in
$Y$
is in
![]() $\Omega _\rho (K)$
then we can assume, without loss of generality, that
$\Omega _\rho (K)$
then we can assume, without loss of generality, that
![]() $\Delta$
is in
$\Delta$
is in
![]() $\widetilde {J}_\rho (K, X)$
and
$\widetilde {J}_\rho (K, X)$
and
![]() $\Delta '$
is adjacent to
$\Delta '$
is adjacent to
![]() $X$
. In that case, the construction of
$X$
. In that case, the construction of
![]() $\widetilde {J}_\rho (K, X)$
ensures that the directed edges of
$\widetilde {J}_\rho (K, X)$
ensures that the directed edges of
![]() $\Delta '$
are pointing towards
$\Delta '$
are pointing towards
![]() $\Delta$
. If
$\Delta$
. If
![]() $X$
and
$X$
and
![]() $Y$
are not in
$Y$
are not in
![]() $\Omega _\rho (K)$
, then we necessarily have
$\Omega _\rho (K)$
, then we necessarily have
![]() $T \in \Omega _\rho (K)$
. In that case, we cannot have
$T \in \Omega _\rho (K)$
. In that case, we cannot have
![]() $|t'| \lt |t|$
, as we would have
$|t'| \lt |t|$
, as we would have
![]() $T' \in \Omega _\rho (K)$
, and this would contradict the connectedness of
$T' \in \Omega _\rho (K)$
, and this would contradict the connectedness of
![]() $\Omega _\rho (K)$
. So all the edges in a circular neighborhood of
$\Omega _\rho (K)$
. So all the edges in a circular neighborhood of
![]() $T$
are pointing towards
$T$
are pointing towards
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Now assume that
![]() $e$
is an edge belonging to a geodesic from a vertex to
$e$
is an edge belonging to a geodesic from a vertex to
![]() $T$
that does not point towards
$T$
that does not point towards
![]() $\mathcal {T}$
. Then, as the last edge of that geodesic is pointing towards
$\mathcal {T}$
. Then, as the last edge of that geodesic is pointing towards
![]() $\mathcal {T}$
, there is necessarily a fork along that geodesic, which means that one of the regions adjacent to
$\mathcal {T}$
, there is necessarily a fork along that geodesic, which means that one of the regions adjacent to
![]() $e$
is in
$e$
is in
![]() $\Omega _\rho (K)$
, and this again contradicts the connectedness of
$\Omega _\rho (K)$
, and this again contradicts the connectedness of
![]() $T_\rho (K)$
.
$T_\rho (K)$
.
We can now infer directly the following property for Bowditch representations.
Proposition 3.16.
Let
![]() $c \in \mathbb {C}$
,
$c \in \mathbb {C}$
,
![]() $[\rho ]$
in
$[\rho ]$
in
![]() $\mathfrak {X}_{BQ}(F_2, \mathrm {SU}(2,1))$
and let
$\mathfrak {X}_{BQ}(F_2, \mathrm {SU}(2,1))$
and let
![]() $M = M(c)$
be the constant defined in (
6
). For any
$M = M(c)$
be the constant defined in (
6
). For any
![]() $K\geqslant M$
, the subgraph
$K\geqslant M$
, the subgraph
![]() $T_\rho (K)$
is finite
$T_\rho (K)$
is finite
![]() $($
in addition to being connected and
$($
in addition to being connected and
![]() $\rho$
-attracting
$\rho$
-attracting
![]() $).$
$).$
Proof.
Given such a representation
![]() $\rho$
, we have that the set
$\rho$
, we have that the set
![]() $\Omega (K)$
is finite, and each
$\Omega (K)$
is finite, and each
![]() $X \in \Omega (K)$
is such that
$X \in \Omega (K)$
is such that
![]() $f(\mathrm {tr} (\rho (X))\gt 0$
and the neighbors around the region
$f(\mathrm {tr} (\rho (X))\gt 0$
and the neighbors around the region
![]() $X$
have exponential growth. Hence, the subgraph
$X$
have exponential growth. Hence, the subgraph
![]() $\widetilde {J}_\rho (K, X)$
is finite. This proves that the subgraph
$\widetilde {J}_\rho (K, X)$
is finite. This proves that the subgraph
![]() $T_\rho (K)$
is a finite union of finite subgraphs and so is finite.
$T_\rho (K)$
is a finite union of finite subgraphs and so is finite.
4. Fibonacci growth
4.1 Fibonacci functions
In this section, we give the definition of the Fibonacci function
![]() $F_v : \Omega \rightarrow \mathbb {N}$
that is associated to a vertex
$F_v : \Omega \rightarrow \mathbb {N}$
that is associated to a vertex
![]() $v = (\alpha, \beta ) \in \mathcal {E}$
, and say what it means for a function
$v = (\alpha, \beta ) \in \mathcal {E}$
, and say what it means for a function
![]() $g \colon \thinspace \Omega \rightarrow [0, \infty )$
to have Fibonacci growth.
$g \colon \thinspace \Omega \rightarrow [0, \infty )$
to have Fibonacci growth.
The map
![]() $F_v$
is constructed by induction on the distance
$F_v$
is constructed by induction on the distance
![]() $d_v (X)$
from a region
$d_v (X)$
from a region
![]() $X \in \Omega$
to
$X \in \Omega$
to
![]() $v$
, which is the minimal graph distance in
$v$
, which is the minimal graph distance in
![]() $\mathcal {E}$
from
$\mathcal {E}$
from
![]() $v$
to a vertex
$v$
to a vertex
![]() $v' = (X,Y)$
. We have naturally
$v' = (X,Y)$
. We have naturally
![]() $d_v (\alpha ) = 0$
and
$d_v (\alpha ) = 0$
and
![]() $d_v (\beta ) = 0$
. Given any region
$d_v (\beta ) = 0$
. Given any region
![]() $Z \neq \alpha, \beta$
, there are precisely two regions
$Z \neq \alpha, \beta$
, there are precisely two regions
![]() $X,Y$
such that
$X,Y$
such that
![]() $X,Y,Z$
are the three regions around a triangle in
$X,Y,Z$
are the three regions around a triangle in
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $d_v (X)\lt d_v (Z)$
and
$d_v (X)\lt d_v (Z)$
and
![]() $d_v (Y) \lt d_v (Z)$
. So we define
$d_v (Y) \lt d_v (Z)$
. So we define
 \begin{equation*}F_v (Z) = \begin{cases} 1 & \mbox {if } d_v (Z)=0, \\ F_v (X) + F_v (Y) & \mbox {if } d_v (Z) \neq 0 \text { and } X, Y \text { are as defined above.} \end{cases}\end{equation*}
\begin{equation*}F_v (Z) = \begin{cases} 1 & \mbox {if } d_v (Z)=0, \\ F_v (X) + F_v (Y) & \mbox {if } d_v (Z) \neq 0 \text { and } X, Y \text { are as defined above.} \end{cases}\end{equation*}
Definition 4.1. Suppose
![]() $g \colon \thinspace \Omega \rightarrow [0, \infty )$
and
$g \colon \thinspace \Omega \rightarrow [0, \infty )$
and
![]() $\Omega ' \subset \Omega$
. Let
$\Omega ' \subset \Omega$
. Let
![]() $v \in \mathcal {E}$
. We say that:
$v \in \mathcal {E}$
. We say that:
-
 $g$
has an upper Fibonacci bound on
$g$
has an upper Fibonacci bound on
 $\Omega '$
if there is some constant
$\Omega '$
if there is some constant
 $\kappa \gt 0$
such that
$\kappa \gt 0$
such that
 $g(X) \leqslant \kappa F_v (X)$
for all
$g(X) \leqslant \kappa F_v (X)$
for all
 $X \in \Omega '$
;
$X \in \Omega '$
; -
 $g$
has a lower Fibonacci bound on
$g$
has a lower Fibonacci bound on
 $\Omega '$
if there is some constant
$\Omega '$
if there is some constant
 $\kappa \gt 0$
such that
$\kappa \gt 0$
such that
 $g(X) \geqslant \kappa F_v (X)$
for all
$g(X) \geqslant \kappa F_v (X)$
for all
 $X \in \Omega '$
;
$X \in \Omega '$
; -
 $g$
has Fibonacci growth on
$g$
has Fibonacci growth on
 $\Omega '$
if it has both upper and lower Fibonacci bound on
$\Omega '$
if it has both upper and lower Fibonacci bound on
 $\Omega '$
.
$\Omega '$
.
The following result will be our basic tool to prove the Fibonacci growth for the logarithm of the norm of trace functions associated to representations in the Bowditch set. This result also shows that the definition of Fibonacci growth is independent of the vertex
![]() $v$
, since the definition only depends on the asymptotic growth of the function and not on the local behavior. In fact, if in the definition above we would use a different function
$v$
, since the definition only depends on the asymptotic growth of the function and not on the local behavior. In fact, if in the definition above we would use a different function
![]() $F_w$
defined with respect to a different vertex
$F_w$
defined with respect to a different vertex
![]() $w$
, then the only difference is that we might have to use different constants.
$w$
, then the only difference is that we might have to use different constants.
Lemma 4.2. (Corollary 2.1.2 in Bowditch [Reference BowditchBow98].) Suppose
![]() $g \colon \thinspace \Omega \rightarrow [0, \infty )$
satisfies an inequality of the form
$g \colon \thinspace \Omega \rightarrow [0, \infty )$
satisfies an inequality of the form
![]() $g(Z) \leqslant g(X)+g(Y)+c$
$g(Z) \leqslant g(X)+g(Y)+c$
![]() $($
respectively,
$($
respectively,
![]() $g(Z) \geqslant g(X)+g(Y)+c)$
for some fixed constant
$g(Z) \geqslant g(X)+g(Y)+c)$
for some fixed constant
![]() $c$
, whenever the regions
$c$
, whenever the regions
![]() $X, Y, Z \in \Omega$
meet at a vertex of the trivalent tree
$X, Y, Z \in \Omega$
meet at a vertex of the trivalent tree
![]() $\mathcal {T}$
. Then
$\mathcal {T}$
. Then
![]() $g$
has lower
$g$
has lower
![]() $($
respectively, upper
$($
respectively, upper
![]() $)$
Fibonacci growth.
$)$
Fibonacci growth.
Another important property of Fibonacci functions is explained by the following result, which relates
![]() $F_v$
to the word length of the elements of
$F_v$
to the word length of the elements of
![]() $\mathcal {S}\subset \Gamma /\!\sim$
; see Section 2.2 for the definition of
$\mathcal {S}\subset \Gamma /\!\sim$
; see Section 2.2 for the definition of
![]() $\Gamma /\!\sim$
. In fact, we can write out explicit representatives in
$\Gamma /\!\sim$
. In fact, we can write out explicit representatives in
![]() $\Gamma$
of elements of
$\Gamma$
of elements of
![]() $\Gamma /\!\sim$
corresponding to given elements of
$\Gamma /\!\sim$
corresponding to given elements of
![]() $\mathcal {S}$
, as we described there. Let
$\mathcal {S}$
, as we described there. Let
![]() $v = (X, Y; T, T') \in \mathcal {E}^{(0)}$
. The regions
$v = (X, Y; T, T') \in \mathcal {E}^{(0)}$
. The regions
![]() $X, Y \in \mathcal {S}$
are represented, respectively, by a pair of free generators
$X, Y \in \mathcal {S}$
are represented, respectively, by a pair of free generators
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
for
$\beta$
for
![]() $\Gamma$
. As explained in Section 2.2, the regions
$\Gamma$
. As explained in Section 2.2, the regions
![]() $T$
and
$T$
and
![]() $T'$
are represented by
$T'$
are represented by
![]() $\alpha \beta$
and
$\alpha \beta$
and
![]() $\alpha \beta ^{-1}$
, respectively, and similarly all other regions in
$\alpha \beta ^{-1}$
, respectively, and similarly all other regions in
![]() $\Omega$
can be written as words in
$\Omega$
can be written as words in
![]() $\alpha ^{\pm 1}$
and
$\alpha ^{\pm 1}$
and
![]() $\beta ^{\pm 1}$
. Note that all the words arising in this way are cyclically reduced. Let
$\beta ^{\pm 1}$
. Note that all the words arising in this way are cyclically reduced. Let
![]() $W(\omega )$
denote the minimal cyclically reduced word length of an element
$W(\omega )$
denote the minimal cyclically reduced word length of an element
![]() $\omega$
with respect to the generating set
$\omega$
with respect to the generating set
![]() $\{\alpha, \beta \}$
. From this we deduce the following.
$\{\alpha, \beta \}$
. From this we deduce the following.
Proposition 4.3.
Suppose
![]() $\{\alpha, \beta \}$
is a set of free generators for
$\{\alpha, \beta \}$
is a set of free generators for
![]() $\Gamma$
corresponding to regions
$\Gamma$
corresponding to regions
![]() $X$
and
$X$
and
![]() $Y$
. Let
$Y$
. Let
![]() $v$
be the vertex
$v$
be the vertex
![]() $v =(X, Y) \in \mathcal {E}^{(0)}$
. If
$v =(X, Y) \in \mathcal {E}^{(0)}$
. If
![]() $\omega _Z \in \widehat \Omega$
corresponds to a region
$\omega _Z \in \widehat \Omega$
corresponds to a region
![]() $Z\in \Omega$
, then
$Z\in \Omega$
, then
![]() $W(\omega _Z) = F_v(Z)$
.
$W(\omega _Z) = F_v(Z)$
.
4.2 Upper and lower Fibonacci growth
For any
![]() $[\rho ] \in \mathfrak {X}$
, we denote by
$[\rho ] \in \mathfrak {X}$
, we denote by
![]() $\phi _\rho \colon \thinspace \Omega \rightarrow \mathbb {C}$
the function
$\phi _\rho \colon \thinspace \Omega \rightarrow \mathbb {C}$
the function
![]() $\phi _\rho (X) := \log | \mathrm {tr} (\rho (X)) |$
. We consider the function
$\phi _\rho (X) := \log | \mathrm {tr} (\rho (X)) |$
. We consider the function
![]() $\phi _\rho ^+ := \max \{ \phi _\rho, 0 \}$
. The purpose of this section is to prove that, if the representation
$\phi _\rho ^+ := \max \{ \phi _\rho, 0 \}$
. The purpose of this section is to prove that, if the representation
![]() $[\rho ]$
is in the Bowditch set
$[\rho ]$
is in the Bowditch set
![]() $\mathfrak {X}_{BQ}$
, then the map
$\mathfrak {X}_{BQ}$
, then the map
![]() $\phi _\rho ^+$
has Fibonacci growth.
$\phi _\rho ^+$
has Fibonacci growth.
First, we show that any representation in
![]() $\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
has upper Fibonacci bound. We will use Lemma3.2.
$\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
has upper Fibonacci bound. We will use Lemma3.2.
Proposition 4.4.
For any
![]() $[\rho ]$
in
$[\rho ]$
in
![]() $\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
, the function
$\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
, the function
![]() $\phi _\rho ^+$
has an upper Fibonacci bound on
$\phi _\rho ^+$
has an upper Fibonacci bound on
![]() $\Omega$
.
$\Omega$
.
Proof.
Let
![]() $v$
be an arbitrary vertex in
$v$
be an arbitrary vertex in
![]() $\mathcal {E}^{(0)}$
. For all regions
$\mathcal {E}^{(0)}$
. For all regions
![]() $Z \in \Omega$
not adjacent to
$Z \in \Omega$
not adjacent to
![]() $v$
, let
$v$
, let
![]() $X, Y$
be the regions adjacent to
$X, Y$
be the regions adjacent to
![]() $Z$
such that
$Z$
such that
![]() $d_u (X) \lt d_u (Z)$
and
$d_u (X) \lt d_u (Z)$
and
![]() $d_u (Y) \lt d_u (Z)$
. Applying Lemma3.2 to the vertex
$d_u (Y) \lt d_u (Z)$
. Applying Lemma3.2 to the vertex
![]() $u = (X,Y; Z, T) \in \mathcal {E}^{(0)}$
, we obtain that
$u = (X,Y; Z, T) \in \mathcal {E}^{(0)}$
, we obtain that
![]() $|z| \leqslant 5 |x| |y|$
and hence
$|z| \leqslant 5 |x| |y|$
and hence
![]() $\phi _\rho ^+ (Z) \leqslant \phi _\rho ^+ (X) + \phi _\rho ^+ (Y) + \log (5)$
. Using Lemma4.2, we can see that
$\phi _\rho ^+ (Z) \leqslant \phi _\rho ^+ (X) + \phi _\rho ^+ (Y) + \log (5)$
. Using Lemma4.2, we can see that
![]() $\phi _\rho ^+$
has an upper Fibonacci bound.
$\phi _\rho ^+$
has an upper Fibonacci bound.
The lower Fibonacci bound is not satisfied for a general representation in
![]() $\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
, but it will be true for representations in the Bowditch set. Recall that a vertex
$\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
, but it will be true for representations in the Bowditch set. Recall that a vertex
![]() $v \in \mathcal {E}^{(0)}$
corresponds to an edge of the trivalent tree
$v \in \mathcal {E}^{(0)}$
corresponds to an edge of the trivalent tree
![]() $\mathcal {T}$
. Hence if we remove such a vertex from
$\mathcal {T}$
. Hence if we remove such a vertex from
![]() $\mathcal {E}$
we split the graph into two connected components. We will refer to properties satisfied on one such component as occurring ‘on one side’. To prove this, we need the following lemma which shows that if a vertex
$\mathcal {E}$
we split the graph into two connected components. We will refer to properties satisfied on one such component as occurring ‘on one side’. To prove this, we need the following lemma which shows that if a vertex
![]() $v$
is ‘attracting on one side’ (meaning that all the geodesics from vertices on one component of
$v$
is ‘attracting on one side’ (meaning that all the geodesics from vertices on one component of
![]() $\mathcal {E} \setminus \{v\}$
are pointing towards
$\mathcal {E} \setminus \{v\}$
are pointing towards
![]() $v$
), then the Fibonacci bound is satisfied for the regions adjacent to that component.
$v$
), then the Fibonacci bound is satisfied for the regions adjacent to that component.
Lemma 4.5.
Let
![]() $[\rho ] \in \mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. Assume that
$[\rho ] \in \mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. Assume that
![]() $v$
is
$v$
is
![]() $\rho$
-attracting on one side, and all the regions adjacent to that component of
$\rho$
-attracting on one side, and all the regions adjacent to that component of
![]() $\mathcal {E} \setminus \{v\}$
have values greater than
$\mathcal {E} \setminus \{v\}$
have values greater than
![]() $C$
. Then there exists
$C$
. Then there exists
![]() $s\gt 0$
such that for all vertices
$s\gt 0$
such that for all vertices
![]() $p \neq v$
in that component, if
$p \neq v$
in that component, if
![]() $X,T,Z'$
are the three regions around
$X,T,Z'$
are the three regions around
![]() $p$
such that
$p$
such that
![]() $d(Z', v) \gt \max \{d(v,T), d(v,X)\}$
, then we have
$d(Z', v) \gt \max \{d(v,T), d(v,X)\}$
, then we have
Proof.
The notation is chosen so that the arrow points away from the region
![]() $Z'$
and towards the region
$Z'$
and towards the region
![]() $Z$
. We have the relation
$Z$
. We have the relation
![]() $z' = z+ \overline {xt} - x y$
. The orientation of the arrow gives that
$z' = z+ \overline {xt} - x y$
. The orientation of the arrow gives that
![]() $|z'| \gt |z|$
. So we have
$|z'| \gt |z|$
. So we have
Now assume that
![]() $|t| \gt |z|$
. This allows us to directly use Lemma3.2, so that
$|t| \gt |z|$
. This allows us to directly use Lemma3.2, so that
This gives
![]() $\log |z'| \gt \log |x| + \log |t| - \log \left ( \frac {C-4}{2C} \right )$
.
$\log |z'| \gt \log |x| + \log |t| - \log \left ( \frac {C-4}{2C} \right )$
.
Note that here we have
![]() $|z'|\gt |y|$
, and hence, by induction, if for a given vertex we have
$|z'|\gt |y|$
, and hence, by induction, if for a given vertex we have
![]() $|t|\gt |z|$
, then for all subsequent vertices we also have that inequality.
$|t|\gt |z|$
, then for all subsequent vertices we also have that inequality.
Finally, we prove that all vertices, except possibly
![]() $v$
, satisfy that inequality. If
$v$
, satisfy that inequality. If
![]() $v$
is such that
$v$
is such that
![]() $|t|\lt |z|$
, then the previous lemma states that
$|t|\lt |z|$
, then the previous lemma states that
![]() $|z| \gt \frac {C}{4} \max \{|x|, |y| \}$
. The two vertices at distance
$|z| \gt \frac {C}{4} \max \{|x|, |y| \}$
. The two vertices at distance
![]() $1$
from
$1$
from
![]() $v$
, which corresponds to
$v$
, which corresponds to
![]() $(x,t,z')$
and
$(x,t,z')$
and
![]() $(y,t,z''),$
satisfy
$(y,t,z''),$
satisfy
![]() $|z'|\gt |y|$
and
$|z'|\gt |y|$
and
![]() $|z''| \gt |x|$
, which is the required inequality to apply the previous reasoning to these two vertices.
$|z''| \gt |x|$
, which is the required inequality to apply the previous reasoning to these two vertices.
We are now going to use Lemma4.5 to prove the lower Fibonacci bound of representations in
![]() $\mathfrak {X}_{BQ}$
.
$\mathfrak {X}_{BQ}$
.
Proposition 4.6.
Let
![]() $[\rho ] \in \mathfrak {X}_{BQ}$
. Then the function
$[\rho ] \in \mathfrak {X}_{BQ}$
. Then the function
![]() $\phi _\rho ^+$
has lower Fibonacci bound on
$\phi _\rho ^+$
has lower Fibonacci bound on
![]() $\Omega$
.a
$\Omega$
.a
Proof.
Let
![]() $[\rho ] \in \mathfrak {X}_{BQ, c}$
. We denote
$[\rho ] \in \mathfrak {X}_{BQ, c}$
. We denote
![]() $M = M(c)$
and we consider the subgraph
$M = M(c)$
and we consider the subgraph
![]() $T_\rho (M)$
, which is finite, connected and
$T_\rho (M)$
, which is finite, connected and
![]() $\rho$
-attracting by Propositions3.15 and 3.16. By construction, all the vertices on the boundary of
$\rho$
-attracting by Propositions3.15 and 3.16. By construction, all the vertices on the boundary of
![]() $T_\rho (M)$
satisfy the hypothesis of Lemma4.5 and hence the map
$T_\rho (M)$
satisfy the hypothesis of Lemma4.5 and hence the map
![]() $\phi _\rho ^+$
has lower Fibonacci growth on each connected component of
$\phi _\rho ^+$
has lower Fibonacci growth on each connected component of
![]() $\mathcal {E} \setminus T_\rho (M)$
. As there are only finitely many such connected components (one for each vertex on the boundary of
$\mathcal {E} \setminus T_\rho (M)$
. As there are only finitely many such connected components (one for each vertex on the boundary of
![]() $T_\rho (M)$
), we can then obtain the lower Fibonacci bound on all of
$T_\rho (M)$
), we can then obtain the lower Fibonacci bound on all of
![]() $\Omega$
.
$\Omega$
.
4.3 Characterizations of Bowditch set
We can now state different characterizations for the representations in the Bowditch set. Our first characterization is a slight reformulation of the definition.
Proposition 4.7.
Let
![]() $[\rho ] \in \mathfrak {X}_c(F_2, \mathrm {SU}(2,1))$
. Then
$[\rho ] \in \mathfrak {X}_c(F_2, \mathrm {SU}(2,1))$
. Then
![]() $[\rho ] \in \mathfrak {X}_{BQ}$
if and only if the following two conditions are satisfied:
$[\rho ] \in \mathfrak {X}_{BQ}$
if and only if the following two conditions are satisfied:
-
(i) for all
 $\gamma \in \mathcal {S}$
, we have
$\gamma \in \mathcal {S}$
, we have
 $f(\mathrm {tr} (\gamma )) \gt 0$
;
$f(\mathrm {tr} (\gamma )) \gt 0$
; -
(ii) for all
 $K \geqslant 0$
, the set
$K \geqslant 0$
, the set
 $\Omega _\rho (K)$
is finite.
$\Omega _\rho (K)$
is finite.
Proof.
For the first condition, Corollary2.7 implies that an element
![]() $A \in \mathrm {SU} (2, 1)$
is loxodromic if and only if
$A \in \mathrm {SU} (2, 1)$
is loxodromic if and only if
![]() $f(\mathrm {tr}(A)) \gt 0$
.
$f(\mathrm {tr}(A)) \gt 0$
.
For the second condition, we can see that if
![]() $[\rho ] \in \mathcal {X}_{BQ, c}$
, then
$[\rho ] \in \mathcal {X}_{BQ, c}$
, then
![]() $\Omega _\rho (M(c))$
is finite and hence
$\Omega _\rho (M(c))$
is finite and hence
![]() $\phi _\rho ^+$
has lower Fibonacci bound. From this it follows that for all
$\phi _\rho ^+$
has lower Fibonacci bound. From this it follows that for all
![]() $K \geqslant M(c)$
we have that the set
$K \geqslant M(c)$
we have that the set
![]() $\Omega _\rho (K)$
is finite, as we wanted. In addition when
$\Omega _\rho (K)$
is finite, as we wanted. In addition when
![]() $0 \leqslant K \lt M(c)$
, then we have the inclusion
$0 \leqslant K \lt M(c)$
, then we have the inclusion
![]() $\Omega _\rho (K) \subset \Omega _\rho (M(c))$
.
$\Omega _\rho (K) \subset \Omega _\rho (M(c))$
.
For the next characterization, we use the fact that
![]() $\mathrm {SU}(2, 1)$
can be identified with the group of orientation-preserving isometries of the complex hyperbolic plane, and relate that to the following notion of well-displacing representations. This will be the link with the notion of Bowditch representation developed by Schlich [Reference SchlichSch22].
$\mathrm {SU}(2, 1)$
can be identified with the group of orientation-preserving isometries of the complex hyperbolic plane, and relate that to the following notion of well-displacing representations. This will be the link with the notion of Bowditch representation developed by Schlich [Reference SchlichSch22].
Recall that for every element
![]() $\varphi \in \mathrm {Isom}(\mathbf {H}_{\mathbb {C}}^2)$
one can consider the displacement
$\varphi \in \mathrm {Isom}(\mathbf {H}_{\mathbb {C}}^2)$
one can consider the displacement
![]() $l(\varphi )$
, which is defined by
$l(\varphi )$
, which is defined by
Recall also that, for any element
![]() $\gamma \in F_2$
, we denote by
$\gamma \in F_2$
, we denote by
![]() $W(\gamma )$
the minimal cyclically reduced word length with respect to some generating set. In these terms, we now prove the following alternative characterization.
$W(\gamma )$
the minimal cyclically reduced word length with respect to some generating set. In these terms, we now prove the following alternative characterization.
Proposition 4.8.
A representation
![]() $[\rho ]$
belongs to
$[\rho ]$
belongs to
![]() $\mathfrak {X}_{BQ}$
if and only if there exists
$\mathfrak {X}_{BQ}$
if and only if there exists
![]() $k, m \gt 0$
such that
$k, m \gt 0$
such that
![]() $|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
$|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
![]() $\gamma \in \mathcal {S}$
.
$\gamma \in \mathcal {S}$
.
Proof.
For the forward direction, we use the fact that if
![]() $[\rho ] \in \mathfrak {X}_{BQ}$
, then Proposition4.6 implies that
$[\rho ] \in \mathfrak {X}_{BQ}$
, then Proposition4.6 implies that
![]() $\phi _\rho ^+$
has lower Fibonacci bound on all of
$\phi _\rho ^+$
has lower Fibonacci bound on all of
![]() $\Omega$
, and hence that there exists
$\Omega$
, and hence that there exists
![]() $\kappa \gt 0$
such that
$\kappa \gt 0$
such that
![]() $\phi _\rho ^+(X) \geqslant \kappa F_v (X)$
for all
$\phi _\rho ^+(X) \geqslant \kappa F_v (X)$
for all
![]() $X \in \Omega$
. Proposition4.3 tells us that for the appropriate
$X \in \Omega$
. Proposition4.3 tells us that for the appropriate
![]() $v \in \mathcal {E}^{(0)}$
we have that
$v \in \mathcal {E}^{(0)}$
we have that
![]() $F_v (\gamma ) = W(\gamma )$
for all
$F_v (\gamma ) = W(\gamma )$
for all
![]() $\gamma \in \mathcal {S}$
. We can use the fact that
$\gamma \in \mathcal {S}$
. We can use the fact that
![]() $\mathrm {log}^+(|\mathrm {tr}(A)|) \leqslant |l(A)|$
for all
$\mathrm {log}^+(|\mathrm {tr}(A)|) \leqslant |l(A)|$
for all
![]() $A \in \mathrm {SU}(2, 1)$
to see that for all
$A \in \mathrm {SU}(2, 1)$
to see that for all
![]() $\gamma \in \mathcal {S}$
we have
$\gamma \in \mathcal {S}$
we have
Conversely, if we have a representation
![]() $\rho$
which satisfies
$\rho$
which satisfies
![]() $|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
$|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
![]() $\gamma \in \mathcal {S}$
, then we will show that
$\gamma \in \mathcal {S}$
, then we will show that
![]() $\rho$
satisfies conditions
$\rho$
satisfies conditions
![]() $(1)$
and
$(1)$
and
![]() $(2)$
from Definition3.12. First, if we have an element
$(2)$
from Definition3.12. First, if we have an element
![]() $\gamma \in \mathcal {S}$
such that
$\gamma \in \mathcal {S}$
such that
![]() $f(\mathrm {tr}(\rho (\gamma ))) \leqslant 0$
, then we can find sequences of regions adjacent to
$f(\mathrm {tr}(\rho (\gamma ))) \leqslant 0$
, then we can find sequences of regions adjacent to
![]() $\gamma$
such that the word length increases, but the length remains bounded. Second, assume that
$\gamma$
such that the word length increases, but the length remains bounded. Second, assume that
![]() $[\rho ] \in \mathfrak {X}_c$
. If the set
$[\rho ] \in \mathfrak {X}_c$
. If the set
![]() $\Omega (M(c))$
is infinite, then we can see that the inequality
$\Omega (M(c))$
is infinite, then we can see that the inequality
![]() $|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
cannot be satisfied for all
$|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
cannot be satisfied for all
![]() $\gamma \in \mathcal {S}$
, because we only have a finite amount of elements with bounded word length.
$\gamma \in \mathcal {S}$
, because we only have a finite amount of elements with bounded word length.
Remark 4.9. Note that the proof above shows that if
![]() $[\rho ] \in \mathfrak {X}_{BQ}$
, then there exists
$[\rho ] \in \mathfrak {X}_{BQ}$
, then there exists
![]() $k\gt 0$
such that
$k\gt 0$
such that
![]() $|l (\rho (\gamma ))| \geqslant k W(\gamma )$
for all
$|l (\rho (\gamma ))| \geqslant k W(\gamma )$
for all
![]() $\gamma \in \mathcal {S}$
. In particular, we do not need the additive constant in the statement of the theorem. On the other hand, the result above is stronger for the converse implication when there is the additive constant, and this is why we are leaving the statement as it is written.
$\gamma \in \mathcal {S}$
. In particular, we do not need the additive constant in the statement of the theorem. On the other hand, the result above is stronger for the converse implication when there is the additive constant, and this is why we are leaving the statement as it is written.
Using this, we can show that all primitive-stable representations are in the Bowditch set. This characterization corresponds to the definition given by Schlich of Bowditch representations, where she proves that Bowditch representations from the free group
![]() $F_2$
into isometry groups of Gromov hyperbolic spaces are primitive stable. So a corollary of the characterization above and of Schlich’s result is that
$F_2$
into isometry groups of Gromov hyperbolic spaces are primitive stable. So a corollary of the characterization above and of Schlich’s result is that
![]() $\mathfrak {X}_{BQ}(F_2, \mathrm {SU}(2,1)) = \mathfrak {X}_{PS}(F_2, \mathrm {SU}(2,1))$
.
$\mathfrak {X}_{BQ}(F_2, \mathrm {SU}(2,1)) = \mathfrak {X}_{PS}(F_2, \mathrm {SU}(2,1))$
.
Proposition 4.10.
Let
![]() $c \in \mathbb {C}$
and
$c \in \mathbb {C}$
and
![]() $K \geqslant M(c)$
, and let
$K \geqslant M(c)$
, and let
![]() $[\rho ] \in \mathfrak {X}_c$
. We have
$[\rho ] \in \mathfrak {X}_c$
. We have
![]() $[\rho ]$
is in
$[\rho ]$
is in
![]() $\mathfrak {X}_{BQ}$
if and only if the subgraph
$\mathfrak {X}_{BQ}$
if and only if the subgraph
![]() $T_\rho (K)$
is finite.
$T_\rho (K)$
is finite.
Proof.
The forward implication follows from Proposition3.16, so we only need to prove that if
![]() $T_\rho (K)$
is finite for
$T_\rho (K)$
is finite for
![]() $K \geqslant M(c)$
, then
$K \geqslant M(c)$
, then
![]() $[\rho ] \in \mathfrak {X}_{BQ}$
. We prove the contrapositive. Suppose
$[\rho ] \in \mathfrak {X}_{BQ}$
. We prove the contrapositive. Suppose
![]() $[\rho ] \notin \mathfrak {X}_{BQ}$
, so then we have two cases.
$[\rho ] \notin \mathfrak {X}_{BQ}$
, so then we have two cases.
The first case is that there exists
![]() $X \in \Omega$
such that
$X \in \Omega$
such that
![]() $\rho (\gamma )$
is not loxodromic (or equivalently that
$\rho (\gamma )$
is not loxodromic (or equivalently that
![]() $f(\mathrm {tr}(\rho (\gamma ))) \leqslant 0$
). In this case the arc
$f(\mathrm {tr}(\rho (\gamma ))) \leqslant 0$
). In this case the arc
![]() $\widetilde {J}(K, X)$
(and hence the subgraph
$\widetilde {J}(K, X)$
(and hence the subgraph
![]() $T_\rho (K)$
) is infinite.
$T_\rho (K)$
) is infinite.
The second case is that the set
![]() $\Omega (K)$
is infinite, so we can see again that the subgraph
$\Omega (K)$
is infinite, so we can see again that the subgraph
![]() $T_\rho (K)$
is infinite because for each
$T_\rho (K)$
is infinite because for each
![]() $X \in \Omega (K)$
the arc
$X \in \Omega (K)$
the arc
![]() $\widetilde {J}(K, X)$
is non-empty.
$\widetilde {J}(K, X)$
is non-empty.
Having addressed both cases, we have proved the proposition.
In the final part of this section we will show why the Bowditch set
![]() $\mathfrak {X}_{BQ}$
strictly contains the set
$\mathfrak {X}_{BQ}$
strictly contains the set
![]() $\mathfrak {X}_{CC}$
of convex cocompact representations in
$\mathfrak {X}_{CC}$
of convex cocompact representations in
![]() $\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. Recall that convex cocompact representations can be defined in many equivalent ways, especially since
$\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. Recall that convex cocompact representations can be defined in many equivalent ways, especially since
![]() $\mathrm {SU}(2,1)$
is a rank
$\mathrm {SU}(2,1)$
is a rank
![]() $1$
Lie group. For example we say that a representation
$1$
Lie group. For example we say that a representation
![]() $[\rho ]\in \mathfrak {X}(F_2, \mathrm {SU}(2,1))$
is convex cocompact if there exists
$[\rho ]\in \mathfrak {X}(F_2, \mathrm {SU}(2,1))$
is convex cocompact if there exists
![]() $k, m \gt 0$
such that
$k, m \gt 0$
such that
![]() $|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
$|l (\rho (\gamma ))| \geqslant k W(\gamma ) - m$
for all
![]() $\gamma \in F_2$
(or, equivalently, if the (any) orbit map
$\gamma \in F_2$
(or, equivalently, if the (any) orbit map
![]() $\tau _\rho$
is a quasi-isometric embedding). We can see from the definition that
$\tau _\rho$
is a quasi-isometric embedding). We can see from the definition that
![]() $\mathfrak {X}_{CC} \subset \mathfrak {X}_{BQ}.$
We now want to show that this is a proper inclusion. We will use a result of Will [Reference WillWil07, Reference WillWil12] that describes a three-dimensional family of discrete, faithful and type-preserving representations of the once-punctured torus in
$\mathfrak {X}_{CC} \subset \mathfrak {X}_{BQ}.$
We now want to show that this is a proper inclusion. We will use a result of Will [Reference WillWil07, Reference WillWil12] that describes a three-dimensional family of discrete, faithful and type-preserving representations of the once-punctured torus in
![]() $\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. These representations will take simple closed curves to loxodromic elements and will map the commutator to a parabolic unipotent element. Let
$\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
. These representations will take simple closed curves to loxodromic elements and will map the commutator to a parabolic unipotent element. Let
![]() $F_2:=\langle \alpha, \beta \rangle$
. Since simple closed curves in
$F_2:=\langle \alpha, \beta \rangle$
. Since simple closed curves in
![]() $S_{1,1}$
correspond to primitive elements of
$S_{1,1}$
correspond to primitive elements of
![]() $F_2$
, the representations described by Will are in the Bowditch set. One can see this using one of our characterizations of
$F_2$
, the representations described by Will are in the Bowditch set. One can see this using one of our characterizations of
![]() $\mathfrak {X}_{BQ}$
, or the equivalence of
$\mathfrak {X}_{BQ}$
, or the equivalence of
![]() $\mathfrak {X}_{BQ}$
with the set of primitive stable representations in
$\mathfrak {X}_{BQ}$
with the set of primitive stable representations in
![]() $\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
implied by Schlich [Reference SchlichSch22]. Remember that the peripheral element corresponds to the commutator, which is not a primitive element. The fact that the commutator
$\mathfrak {X}(F_2, \mathrm {SU}(2,1))$
implied by Schlich [Reference SchlichSch22]. Remember that the peripheral element corresponds to the commutator, which is not a primitive element. The fact that the commutator
![]() $[\alpha, \beta ]$
is mapped to a unipotent element by Will’s representations prevents them from being convex cocompact representations. If one would like to see other examples of representations that are in
$[\alpha, \beta ]$
is mapped to a unipotent element by Will’s representations prevents them from being convex cocompact representations. If one would like to see other examples of representations that are in
![]() $\mathfrak {X}_{BQ} \setminus \mathfrak {X}_{CC}$
and such that the peripheral element is mapped to a parabolic non-unipotent element, one can use the work of Falbel and Parker [Reference Falbel and ParkerFP03], Falbel and Koseleff [Reference Falbel and KoseleffFK02b, Reference Falbel and KoseleffFK02a] or Parker and Gusevskii [Reference Gusevskii and ParkerGP03, Reference Gusevskii and ParkerGP00]. See also Will [Reference WillWil16] for a discussion of these references. These examples imply the following result.
$\mathfrak {X}_{BQ} \setminus \mathfrak {X}_{CC}$
and such that the peripheral element is mapped to a parabolic non-unipotent element, one can use the work of Falbel and Parker [Reference Falbel and ParkerFP03], Falbel and Koseleff [Reference Falbel and KoseleffFK02b, Reference Falbel and KoseleffFK02a] or Parker and Gusevskii [Reference Gusevskii and ParkerGP03, Reference Gusevskii and ParkerGP00]. See also Will [Reference WillWil16] for a discussion of these references. These examples imply the following result.
Proposition 4.11.
The set
![]() $\mathfrak {X}_{BQ}$
strictly contains the set of convex cocompact representations
$\mathfrak {X}_{BQ}$
strictly contains the set of convex cocompact representations
![]() $\mathfrak {X}_{CC}$
.
$\mathfrak {X}_{CC}$
.
4.4 Openness and proper discontinuity
In this section we prove that the set
![]() $\mathfrak {X}_{BQ}$
is open and the group
$\mathfrak {X}_{BQ}$
is open and the group
![]() $\mathrm {Out}(F_2)$
acts properly discontinuously on it. First we prove the following lemma which will imply the openness of
$\mathrm {Out}(F_2)$
acts properly discontinuously on it. First we prove the following lemma which will imply the openness of
![]() $\mathfrak {X}_{BQ, c}$
.
$\mathfrak {X}_{BQ, c}$
.
Lemma 4.12.
Let
![]() $c \in C$
and let
$c \in C$
and let
![]() $K \geqslant M(c)$
. For each
$K \geqslant M(c)$
. For each
![]() $[\rho ] \in \mathfrak {X}_{BQ, c}$
, if
$[\rho ] \in \mathfrak {X}_{BQ, c}$
, if
![]() $T_\rho (K)$
is non-empty, there exists a neighborhood
$T_\rho (K)$
is non-empty, there exists a neighborhood
![]() $U_\rho$
of
$U_\rho$
of
![]() $[\rho ]$
in
$[\rho ]$
in
![]() $\mathfrak {X}_c$
such that, for all
$\mathfrak {X}_c$
such that, for all
![]() $[\sigma ] \in U_\rho$
, the subgraph
$[\sigma ] \in U_\rho$
, the subgraph
![]() $T_\sigma (K)$
is contained in
$T_\sigma (K)$
is contained in
![]() $T_\rho (K)$
.
$T_\rho (K)$
.
Proof.
Let
![]() $[\rho ] \in \mathfrak {X}_{BQ, c}$
and let
$[\rho ] \in \mathfrak {X}_{BQ, c}$
and let
![]() $K \gt M(c)$
such that
$K \gt M(c)$
such that
![]() $T_\rho (K)$
is non-empty. First, it is easy to see that, for
$T_\rho (K)$
is non-empty. First, it is easy to see that, for
![]() $\sigma$
close enough to
$\sigma$
close enough to
![]() $\rho$
, the subgraphs
$\rho$
, the subgraphs
![]() $T_\sigma (K)$
and
$T_\sigma (K)$
and
![]() $T_\rho (K)$
have non-empty intersection.
$T_\rho (K)$
have non-empty intersection.
Now consider the set
![]() $V \subset \mathcal {E}^{(0)}$
of vertices of
$V \subset \mathcal {E}^{(0)}$
of vertices of
![]() $\mathcal {E}$
which are on the boundary of
$\mathcal {E}$
which are on the boundary of
![]() $T_\rho (K)$
. Let
$T_\rho (K)$
. Let
![]() $v \in V$
. We can show that if
$v \in V$
. We can show that if
![]() $[\sigma ] \in \mathfrak {X}_c$
is close enough to
$[\sigma ] \in \mathfrak {X}_c$
is close enough to
![]() $[\rho ]$
, then
$[\rho ]$
, then
![]() $v$
is also not in the interior of
$v$
is also not in the interior of
![]() $T_\sigma (K)$
. From the definition of
$T_\sigma (K)$
. From the definition of
![]() $T_\rho (K)$
we can see that if
$T_\rho (K)$
we can see that if
![]() $v = (X, X')$
, then we have
$v = (X, X')$
, then we have
![]() $| \mathrm {tr}(\rho (X))| \gt K$
or
$| \mathrm {tr}(\rho (X))| \gt K$
or
![]() $| \mathrm {tr} (\rho (X'))| \gt K$
. If we choose
$| \mathrm {tr} (\rho (X'))| \gt K$
. If we choose
![]() $\sigma$
close enough to
$\sigma$
close enough to
![]() $\rho$
, then we can show that the same inequality will be true for
$\rho$
, then we can show that the same inequality will be true for
![]() $\sigma$
as well. Since the subgraph
$\sigma$
as well. Since the subgraph
![]() $T_\rho (K)$
is finite, there is only a finite number of vertices in
$T_\rho (K)$
is finite, there is only a finite number of vertices in
![]() $V$
, so we can choose
$V$
, so we can choose
![]() $\sigma$
close enough to
$\sigma$
close enough to
![]() $\rho$
such that any vertex
$\rho$
such that any vertex
![]() $v \in V$
is not on the interior of
$v \in V$
is not on the interior of
![]() $T_\sigma (K)$
.
$T_\sigma (K)$
.
Now, since
![]() $T_\sigma (K)$
is connected and
$T_\sigma (K)$
is connected and
![]() $T_\sigma (K) \cap T_\rho (K)$
is non-empty, we have that the subgraph
$T_\sigma (K) \cap T_\rho (K)$
is non-empty, we have that the subgraph
![]() $T_\sigma (K)$
is contained in
$T_\sigma (K)$
is contained in
![]() $T_\rho (K)$
.
$T_\rho (K)$
.
The last result of this paper proves proper discontinuity for the action of
![]() $\mathrm {Out}(F_2)$
on
$\mathrm {Out}(F_2)$
on
![]() $\mathfrak {X}_{BQ, c}$
.
$\mathfrak {X}_{BQ, c}$
.
Theorem 4.13.
The set
![]() $\mathfrak {X}_{BQ, c}$
is open in
$\mathfrak {X}_{BQ, c}$
is open in
![]() $\mathfrak {X}_c$
and the action of
$\mathfrak {X}_c$
and the action of
![]() $\mathrm {Out}(F_2)$
is properly discontinuous on
$\mathrm {Out}(F_2)$
is properly discontinuous on
![]() $\mathfrak {X}_{BQ, c}$
.
$\mathfrak {X}_{BQ, c}$
.
Proof.
The previous lemma directly implies openness, using the characterization of representations in
![]() $\mathfrak {X}_{BQ, c}$
given by Proposition4.10.
$\mathfrak {X}_{BQ, c}$
given by Proposition4.10.
In order to prove that the action of
![]() $\mathrm {Out}(F_2)$
is properly discontinuous, let
$\mathrm {Out}(F_2)$
is properly discontinuous, let
![]() $\mathsf {C}$
be a compact subset of
$\mathsf {C}$
be a compact subset of
![]() $\mathfrak {X}_{BQ, c}$
. We want to prove that the set
$\mathfrak {X}_{BQ, c}$
. We want to prove that the set
is finite.
Let
![]() $K \geqslant M(c)$
be such that, for any
$K \geqslant M(c)$
be such that, for any
![]() $[\rho ] \in \mathsf {C}$
, the tree
$[\rho ] \in \mathsf {C}$
, the tree
![]() $T_\rho (K)$
is non-empty. Now around each element of
$T_\rho (K)$
is non-empty. Now around each element of
![]() $\mathsf {C}$
there exists a neighborhood
$\mathsf {C}$
there exists a neighborhood
![]() $U_\rho$
given by the previous lemma. So we have that the set
$U_\rho$
given by the previous lemma. So we have that the set
![]() $(U_{\sigma })_{[\sigma ] \in \mathsf {C}}$
is an open covering of
$(U_{\sigma })_{[\sigma ] \in \mathsf {C}}$
is an open covering of
![]() $\mathsf {C}$
. Using the compactness of
$\mathsf {C}$
. Using the compactness of
![]() $\mathsf {C}$
, we take a finite subcover
$\mathsf {C}$
, we take a finite subcover
![]() $(U_{\rho _i})_{i\in I}$
, where
$(U_{\rho _i})_{i\in I}$
, where
![]() $I$
is a finite set.
$I$
is a finite set.
Now, for each element
![]() $\rho _i$
, we take the tree
$\rho _i$
, we take the tree
![]() $T_{\rho _i} (K)$
and consider the union
$T_{\rho _i} (K)$
and consider the union
By construction, for each element
![]() $[\sigma ] \in \mathsf {C}$
, the subgraph
$[\sigma ] \in \mathsf {C}$
, the subgraph
![]() $T_\sigma (K)$
is contained in
$T_\sigma (K)$
is contained in
![]() $\mathcal {T}(K)$
. Since the subgraph
$\mathcal {T}(K)$
. Since the subgraph
![]() $\mathcal {T}(K)$
is a finite union of finite subgraphs, it is itself finite. It follows that the set
$\mathcal {T}(K)$
is a finite union of finite subgraphs, it is itself finite. It follows that the set
is finite. Finally, as
![]() $T_{g\sigma } (K) = g T_\sigma (K)$
, we have that
$T_{g\sigma } (K) = g T_\sigma (K)$
, we have that
![]() $\Gamma _{\mathsf {C}} \subset \Gamma _1$
, and hence
$\Gamma _{\mathsf {C}} \subset \Gamma _1$
, and hence
![]() $\Gamma _{\mathsf {C}}$
is finite, which proves that
$\Gamma _{\mathsf {C}}$
is finite, which proves that
![]() $\mathrm {Out} (F_2)$
acts on
$\mathrm {Out} (F_2)$
acts on
![]() $\mathfrak {X}_{BQ, c}$
properly discontinuously.
$\mathfrak {X}_{BQ, c}$
properly discontinuously.
Appendix A. Computations
A.1
 $f=0$
case
$f=0$
case
Recall the set-up from Section 3.3. Let
![]() $\alpha$
be the region in
$\alpha$
be the region in
![]() $\mathcal {C}^{(0)}$
which will serve as our central region. The neighbors are all of the form
$\mathcal {C}^{(0)}$
which will serve as our central region. The neighbors are all of the form
![]() $\gamma _n = \alpha ^n \beta$
for all
$\gamma _n = \alpha ^n \beta$
for all
![]() $n \in \mathbb {N}$
. Let
$n \in \mathbb {N}$
. Let
![]() $[\rho ] \in \mathfrak {X}_c$
be a representation, with
$[\rho ] \in \mathfrak {X}_c$
be a representation, with
![]() $c \in \mathbb {C}$
(and
$c \in \mathbb {C}$
(and
![]() $P,Q \in \mathbb {R}$
). Let
$P,Q \in \mathbb {R}$
). Let
![]() $x = \mathrm {tr} (\rho (\alpha ))$
and consider the sequence
$x = \mathrm {tr} (\rho (\alpha ))$
and consider the sequence
![]() $u_n = \mathrm {tr} (\rho (\gamma _n))$
. The trace identity gives, for all
$u_n = \mathrm {tr} (\rho (\gamma _n))$
. The trace identity gives, for all
![]() $n \in \mathbb {Z}$
, the following relation:
$n \in \mathbb {Z}$
, the following relation:
To study the solutions of this recurrence relation we consider the matrix
 \begin{equation*}M_x = \left(\begin{matrix} x & - \overline x & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{matrix}\right),\end{equation*}
\begin{equation*}M_x = \left(\begin{matrix} x & - \overline x & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{matrix}\right),\end{equation*}
and we define
 \begin{equation*}X_n = \left(\begin{matrix} u_{n+2} \\ u_{n+1} \\ u_n \end{matrix}\right) \in \mathbb {C}^3,\end{equation*}
\begin{equation*}X_n = \left(\begin{matrix} u_{n+2} \\ u_{n+1} \\ u_n \end{matrix}\right) \in \mathbb {C}^3,\end{equation*}
so that we have
![]() $X_{n+1} = M_x X_n$
. The matrix
$X_{n+1} = M_x X_n$
. The matrix
![]() $M_x$
is conjugate to a matrix in
$M_x$
is conjugate to a matrix in
![]() $\textrm {SU} (2,1)$
.
$\textrm {SU} (2,1)$
.
Given a matrix
![]() $A\in \textrm {SU} (2,1)$
, recall that its characteristic polynomial is given by
$A\in \textrm {SU} (2,1)$
, recall that its characteristic polynomial is given by
![]() $\chi _A(x) = x^3 - t x^2 + \overline t x -1$
, where
$\chi _A(x) = x^3 - t x^2 + \overline t x -1$
, where
![]() $t=\mathrm {tr}(A)$
. The resultant of
$t=\mathrm {tr}(A)$
. The resultant of
![]() $\chi _A$
and its derivative tells us when
$\chi _A$
and its derivative tells us when
![]() $\chi _A$
has multiple roots, and hence when
$\chi _A$
has multiple roots, and hence when
![]() $A$
has an eigenvalue with multiplicity greater than
$A$
has an eigenvalue with multiplicity greater than
![]() $1$
. Recall also the definition of the function
$1$
. Recall also the definition of the function
![]() $f\colon \thinspace \mathbb {C}\longrightarrow \mathbb {R}$
by
$f\colon \thinspace \mathbb {C}\longrightarrow \mathbb {R}$
by
Lemma A.1.
If
![]() $f(x)= 0$
, then the coefficients of the matrix
$f(x)= 0$
, then the coefficients of the matrix
![]() $M_x^n$
grow at most quadratically in
$M_x^n$
grow at most quadratically in
![]() $n$
, and hence the growth of the sequence
$n$
, and hence the growth of the sequence
![]() $(X_n)_{n\in \mathbb {Z}}$
, and hence of the sequence
$(X_n)_{n\in \mathbb {Z}}$
, and hence of the sequence
![]() $(u_n)_{n\in \mathbb {Z}}$
, is at most quadratic.
$(u_n)_{n\in \mathbb {Z}}$
, is at most quadratic.
Proof.
Since
![]() $f(x)=0$
there are repeated roots to the characteristic polynomial and all roots have modulus
$f(x)=0$
there are repeated roots to the characteristic polynomial and all roots have modulus
![]() $1$
. So, up to conjugation (potentially in
$1$
. So, up to conjugation (potentially in
![]() $\mathrm {GL}(3,\mathbb {C})$
), the matrix
$\mathrm {GL}(3,\mathbb {C})$
), the matrix
![]() $M_x$
is of the form
$M_x$
is of the form
 \begin{equation*}\left ( \begin{array}{c@{\quad}c@{\quad}c} a & 1 & 0 \\ 0 & a & 1 \\ 0 & 0 & a \\ \end{array} \right )\text { or }\left ( \begin{array}{c@{\quad}c@{\quad}c} a & 1 & 0 \\ 0 & a & 0 \\ 0 & 0 & \frac {1}{a^2} \\ \end{array} \right ),\end{equation*}
\begin{equation*}\left ( \begin{array}{c@{\quad}c@{\quad}c} a & 1 & 0 \\ 0 & a & 1 \\ 0 & 0 & a \\ \end{array} \right )\text { or }\left ( \begin{array}{c@{\quad}c@{\quad}c} a & 1 & 0 \\ 0 & a & 0 \\ 0 & 0 & \frac {1}{a^2} \\ \end{array} \right ),\end{equation*}
where
![]() $a$
is a cube root of unity. In the first case,
$a$
is a cube root of unity. In the first case,
 \begin{equation*}M_x^n=\left ( \begin{array}{c@{\quad}c@{\quad}c} a^n & na^{n-1} & n\left (\frac {n-1}{2}\right )a^{n-2} \\ 0 & a^n & na^{n-1} \\ 0 & 0 & a^n \\ \end{array} \right ),\end{equation*}
\begin{equation*}M_x^n=\left ( \begin{array}{c@{\quad}c@{\quad}c} a^n & na^{n-1} & n\left (\frac {n-1}{2}\right )a^{n-2} \\ 0 & a^n & na^{n-1} \\ 0 & 0 & a^n \\ \end{array} \right ),\end{equation*}
and so the matrix entries are bounded above by
![]() $n\left (\frac {n-1}{2}\right )$
. In the second case,
$n\left (\frac {n-1}{2}\right )$
. In the second case,
 \begin{equation*}M_x^n=\left ( \begin{array}{c@{\quad}c@{\quad}c} a^n & na^{n-1} & 0 \\ 0 & a^n & 0 \\ 0 & 0 & a^{-2n} \\ \end{array} \right ),\end{equation*}
\begin{equation*}M_x^n=\left ( \begin{array}{c@{\quad}c@{\quad}c} a^n & na^{n-1} & 0 \\ 0 & a^n & 0 \\ 0 & 0 & a^{-2n} \\ \end{array} \right ),\end{equation*}
and so the entries are bounded above by
![]() $n$
. In both cases the growth is at most quadratic.
$n$
. In both cases the growth is at most quadratic.
A.2
 $P=6$
case
$P=6$
case
Recall from earlier that
We can identify the quadruple
![]() $(x, u_{n+1}, u_{n+2}, \overline {u_n})$
as the character of a representation in
$(x, u_{n+1}, u_{n+2}, \overline {u_n})$
as the character of a representation in
![]() $\mathfrak {X}_c$
, and hence the quadruple will satisfy the equations for
$\mathfrak {X}_c$
, and hence the quadruple will satisfy the equations for
![]() $P$
and
$P$
and
![]() $Q$
. For large
$Q$
. For large
![]() $n$
, the quadruple is arbitrarily close to a vector of the form
$n$
, the quadruple is arbitrarily close to a vector of the form
![]() $(x, B, B{\bar \lambda }{\lambda ^{-1}}, \overline {B}{\bar \lambda }{\lambda ^{-1}})$
for
$(x, B, B{\bar \lambda }{\lambda ^{-1}}, \overline {B}{\bar \lambda }{\lambda ^{-1}})$
for
![]() $\lambda \in \mathbb {C}^*$
and
$\lambda \in \mathbb {C}^*$
and
![]() $B\in \mathbb {C}$
.
$B\in \mathbb {C}$
.
Therefore, this quadruple satisfies the equations for
![]() $P$
and
$P$
and
![]() $Q$
:
$Q$
:
 \begin{align*} P & = |x|^2 |B|^2 + |x|^2 + |B|^2+|B|^2+|B|^2 - 2 \Re (x B {\lambda }{\bar \lambda }^{-1} \overline {B}) - 2 \Re (\overline {x} B {\bar \lambda }{\lambda ^{-1}} \overline {B} ) -2 \\ & = |B|^2 ( |x|^2 - 4 \Re ( x {\lambda }{ \bar \lambda }^{-1} ) +3) - 3 + |x|^2. \end{align*}
\begin{align*} P & = |x|^2 |B|^2 + |x|^2 + |B|^2+|B|^2+|B|^2 - 2 \Re (x B {\lambda }{\bar \lambda }^{-1} \overline {B}) - 2 \Re (\overline {x} B {\bar \lambda }{\lambda ^{-1}} \overline {B} ) -2 \\ & = |B|^2 ( |x|^2 - 4 \Re ( x {\lambda }{ \bar \lambda }^{-1} ) +3) - 3 + |x|^2. \end{align*}
So we obtain an expression for
![]() $|B|$
in terms of
$|B|$
in terms of
![]() $P$
and
$P$
and
![]() $x$
:
$x$
:
Recall that
![]() $x = \lambda + {\bar \lambda }{\lambda ^{-1}} + {\bar \lambda }^{-1}$
and
$x = \lambda + {\bar \lambda }{\lambda ^{-1}} + {\bar \lambda }^{-1}$
and
![]() $|x|^2 = x \overline {x}$
. Letting
$|x|^2 = x \overline {x}$
. Letting
![]() $P = 6$
, and
$P = 6$
, and
![]() $\lambda =re^{is}$
we derive (using Mathematica):
$\lambda =re^{is}$
we derive (using Mathematica):
This expression is well-defined for every value of
![]() $r$
and
$r$
and
![]() $s$
except where
$s$
except where
![]() $r=1$
and
$r=1$
and
![]() $s=0, 2\pi /3,$
or
$s=0, 2\pi /3,$
or
![]() $4\pi /3$
. In those cases the numerator and denominator are both 0.
$4\pi /3$
. In those cases the numerator and denominator are both 0.
However, for every fixed value of
![]() $s$
not equal to
$s$
not equal to
![]() $0, 2\pi /3$
or
$0, 2\pi /3$
or
![]() $4\pi /3$
, as
$4\pi /3$
, as
![]() $r\longrightarrow 1$
the limit of
$r\longrightarrow 1$
the limit of
![]() $|B|^2$
is 1. But for
$|B|^2$
is 1. But for
![]() $s$
equal to any of
$s$
equal to any of
![]() $0, 2\pi /3, 4\pi /3$
, the limit as
$0, 2\pi /3, 4\pi /3$
, the limit as
![]() $r\longrightarrow 1$
is
$r\longrightarrow 1$
is
![]() $-3$
. So when
$-3$
. So when
![]() $\lambda$
converges to an element of
$\lambda$
converges to an element of
![]() $\zeta _3$
, despite both the numerator and the denominator going to
$\zeta _3$
, despite both the numerator and the denominator going to
![]() $0$
, the expression stays bounded (see Figure 7). If this was not the case, then we would not have the situation that, for all fixed value of
$0$
, the expression stays bounded (see Figure 7). If this was not the case, then we would not have the situation that, for all fixed value of
![]() $s$
not equal to
$s$
not equal to
![]() $0, 2\pi /3$
or
$0, 2\pi /3$
or
![]() $4\pi /3$
, as
$4\pi /3$
, as
![]() $r\longrightarrow 1$
the limit of
$r\longrightarrow 1$
the limit of
![]() $|B|^2$
is
$|B|^2$
is
![]() $1$
.
$1$
.

Figure 7. Graph of
![]() $|B|^2$
when
$|B|^2$
when
![]() $P=6$
.
$P=6$
.
A.3
 $P\gt 6$
case
$P\gt 6$
case
If
![]() $P \gt 6$
, then the expression for
$P \gt 6$
, then the expression for
![]() $|B|^2$
as a function of
$|B|^2$
as a function of
![]() $\lambda$
is unbounded when
$\lambda$
is unbounded when
![]() $\lambda$
gets close to
$\lambda$
gets close to
![]() $1$
. In that case, we also need to use the expression for
$1$
. In that case, we also need to use the expression for
![]() $Q$
which, after simplification, is
$Q$
which, after simplification, is
 \begin{align*} Q = & |B|^4 \left (5 + |x|^2 + 2 \Re \left ( 2 (\frac {\bar \lambda }{\lambda })^3- 2 \overline x \frac {\bar \lambda }{\lambda } - x (\frac {\bar \lambda }{\lambda })^2 \right ) \right ) \\ & + |B|^2 \left ( |x|^4+3|x|^2-18+2\Re \left ( 2 x^2 \frac {\bar \lambda }{\lambda }-3 x (\frac {\bar \lambda }{\lambda })^2+6 \overline x \frac {\bar \lambda }{\lambda } - 2 |x|^2 \overline x \frac {\bar \lambda }{\lambda }+\overline x^2( \frac {\bar \lambda }{\lambda })^2-x^3 \right ) \right ) \\ & + 9 - 6|x|^2+2\Re (x^3). \end{align*}
\begin{align*} Q = & |B|^4 \left (5 + |x|^2 + 2 \Re \left ( 2 (\frac {\bar \lambda }{\lambda })^3- 2 \overline x \frac {\bar \lambda }{\lambda } - x (\frac {\bar \lambda }{\lambda })^2 \right ) \right ) \\ & + |B|^2 \left ( |x|^4+3|x|^2-18+2\Re \left ( 2 x^2 \frac {\bar \lambda }{\lambda }-3 x (\frac {\bar \lambda }{\lambda })^2+6 \overline x \frac {\bar \lambda }{\lambda } - 2 |x|^2 \overline x \frac {\bar \lambda }{\lambda }+\overline x^2( \frac {\bar \lambda }{\lambda })^2-x^3 \right ) \right ) \\ & + 9 - 6|x|^2+2\Re (x^3). \end{align*}
Replacing the expression of
![]() $|B|^2$
in terms of
$|B|^2$
in terms of
![]() $P$
and
$P$
and
![]() $\lambda$
found previously and substituting
$\lambda$
found previously and substituting
![]() $\lambda =re^{is}$
, we have an expression relating
$\lambda =re^{is}$
, we have an expression relating
![]() $Q, P$
and
$Q, P$
and
![]() $\lambda$
(derived using Mathematica):
$\lambda$
(derived using Mathematica):
Amazingly
![]() $Q_P(\lambda )$
does not depend on
$Q_P(\lambda )$
does not depend on
![]() $s$
at all. Letting
$s$
at all. Letting
![]() $r\longrightarrow 1$
we see that
$r\longrightarrow 1$
we see that
![]() $Q_P (\lambda ) \longrightarrow \frac {P^2}{4}$
.
$Q_P (\lambda ) \longrightarrow \frac {P^2}{4}$
.
Acknowledgments
The authors acknowledge support from U.S. National Science Foundation grant nos. DMS 1107452, 1107263, 1107367 RNMS: ‘Geometric Structures and Representation Varieties’ (the GEAR Network). S. Lawton was supported by the Simons Foundation. S. Maloni was partially supported by U.S. National Science Foundation grant no. DMS-1848346 (NSF CAREER). Lastly, we thank the referees for many helpful suggestions which improved the paper.
Conflicts of Interest
None
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.