We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We inspect the relationship between relative Fourier multipliers on noncommutative Lebesgue–Orlicz spaces of a discrete group 
$\Gamma$ and relative Toeplitz-Schur multipliers on Schatten–von-Neumann–Orlicz classes. Four applications are given: lacunary sets, unconditional Schauder bases for the subspace of a Lebesgue space determined by a given spectrum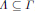 
$\Lambda \,\subseteq \,\Gamma$, the norm of the Hilbert transformand the Riesz projection on Schatten–von-Neumann classes with exponent a power of 2, and the norm of Toeplitz Schur multipliers on Schatten–von-Neumann classes with exponent less than 1.
