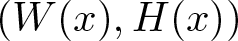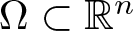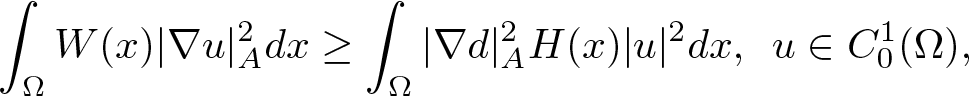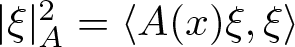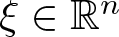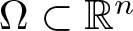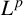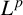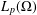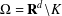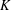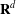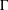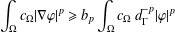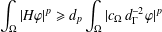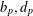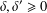4 results
Hardy and Rellich Inequalities with Bessel Pairs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 31 March 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME
 $\boldsymbol {L^p}$
-HARDY AND
$\boldsymbol {L^p}$
-HARDY AND
 $\boldsymbol {L^p}$
-RELLICH TYPE INEQUALITIES WITH REMAINDER TERMS
$\boldsymbol {L^p}$
-RELLICH TYPE INEQUALITIES WITH REMAINDER TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 79-98
- Print publication:
- August 2022
-
- Article
- Export citation
New sharp Hardy and Rellich type inequalities on Cartan–Hadamard manifolds and their improvements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 2952-2981
- Print publication:
- December 2020
-
- Article
- Export citation
HARDY AND RELLICH INEQUALITIES ON THE COMPLEMENT OF CONVEX SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 98-119
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation