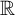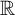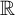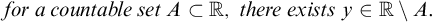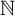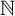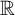The uncountability of 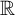$\mathbb {R}$ is one of its most basic properties, known far outside of mathematics. Cantor’s 1874 proof of the uncountability of 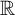$\mathbb {R}$ even appears in the very first paper on set theory, i.e., a historical milestone. In this paper, we study the uncountability of 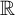${\mathbb R}$ in Kohlenbach’s higher-order Reverse Mathematics (RM for short), in the guise of the following principle:

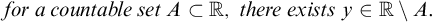$$\begin{align*}\mathit{for \ a \ countable \ set } \ A\subset \mathbb{R}, \mathit{\ there \ exists } \ y\in \mathbb{R}\setminus A. \end{align*}$$

An important conceptual observation is that the usual definition of countable set—based on injections or bijections to 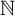${\mathbb N}$—does not seem suitable for the RM-study of mainstream mathematics; we also propose a suitable (equivalent over strong systems) alternative definition of countable set, namely union over 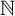${\mathbb N}$ of finite sets; the latter is known from the literature and closer to how countable sets occur ‘in the wild’. We identify a considerable number of theorems that are equivalent to the centred theorem based on our alternative definition. Perhaps surprisingly, our equivalent theorems involve most basic properties of the Riemann integral, regulated or bounded variation functions, Blumberg’s theorem, and Volterra’s early work circa 1881. Our equivalences are also robust, promoting the uncountability of 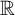${\mathbb R}$ to the status of ‘big’ system in RM.

Sampling efficiency (p), estimated from the Zippin depletion model and the percentage of fish obtained during first runs (single-pass electrofishing), which is also named relative abundance (C1), calculated as the ratio of C1 to estimated density for a site (Ce), were analysed in five contiguous sites in a small lowland stream in Poland over 23 years. The sampled reach was unregulated during the first decade of the study period, but regulated by weirs and sluices in the latter 13 years. The sites were populated with 17 fish species during this period. Sampling efficiency p calculated for all species did not differ significantly between the five sites in any given year, between benthic and non-benthic species, or between the natural and regulated periods. Differences in p were only observed between some species. C1 differed significantly between large and small species and, except for roach, was not dependent on the number of runs. Results indicate a high stability of both sampling indices in this small stream, despite changes in channel morphology after regulation: information which could be useful for future sampling research in streams.