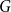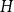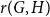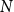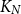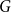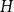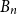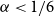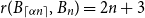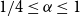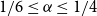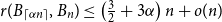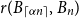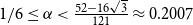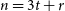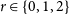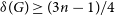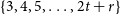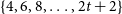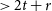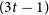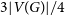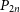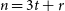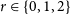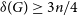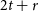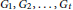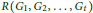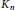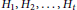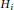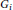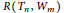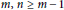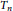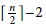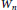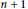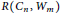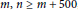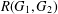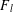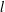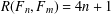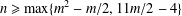6 results
ON THE RAMSEY NUMBERS OF TREE GRAPHS VERSUS CERTAIN GENERALISED WHEEL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 08 October 2024, pp. 564-565
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
On a conjecture of Conlon, Fox, and Wigderson
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 432-445
-
- Article
-
- You have access
- HTML
- Export citation
Monochromatic paths and cycles in 2-edge-coloured graphs with large minimum degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 14 June 2021, pp. 109-122
-
- Article
- Export citation
Ramsey Number of Wheels Versus Cycles and Trees
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 1 / 01 March 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-196
- Print publication:
- 01 March 2016
-
- Article
-
- You have access
- Export citation
A NOTE ON RAMSEY NUMBERS FOR FANS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 13 May 2015, pp. 19-23
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
RAMSEY NUMBERS FOR TREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 164-176
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation