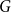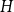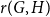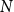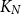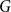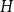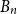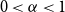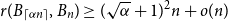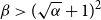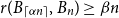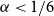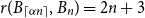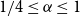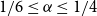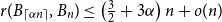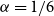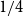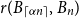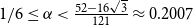1. Introduction
For graphs
![]() $G$
and
$G$
and
![]() $H$
, the Ramsey number
$H$
, the Ramsey number
![]() $r(G,H)$
is the smallest positive integer
$r(G,H)$
is the smallest positive integer
![]() $N$
such that any red/blue edge colouring of the complete graph
$N$
such that any red/blue edge colouring of the complete graph
![]() $K_N$
contains either a red
$K_N$
contains either a red
![]() $G$
or a blue
$G$
or a blue
![]() $H$
. A central problem in extremal graph theory is to determine the Ramsey number
$H$
. A central problem in extremal graph theory is to determine the Ramsey number
![]() $r(G,H)$
.
$r(G,H)$
.
Let
![]() $B_{n}^{(k)}$
be the book graph consisting of
$B_{n}^{(k)}$
be the book graph consisting of
![]() $n$
copies of
$n$
copies of
![]() $K_{k+1}$
, all sharing a common
$K_{k+1}$
, all sharing a common
![]() $K_k$
. We always call
$K_k$
. We always call
![]() $n$
the size of the book. When
$n$
the size of the book. When
![]() $k=2$
, we write
$k=2$
, we write
![]() $B_{n}$
instead of
$B_{n}$
instead of
![]() $B_{n}^{(2)}$
. Books have attracted a great deal of attention in graph Ramsey theory, see, for example, the recent breakthrough of Campos, Griffiths, Morris and Sahasrabudhe [Reference Campos, Griffiths, Morris and Sahasrabudhe1].
$B_{n}^{(2)}$
. Books have attracted a great deal of attention in graph Ramsey theory, see, for example, the recent breakthrough of Campos, Griffiths, Morris and Sahasrabudhe [Reference Campos, Griffiths, Morris and Sahasrabudhe1].
For the diagonal Ramsey number of books, Erdős, Faudree, Rousseau and Schelp [Reference Erdős, Faudree, Rousseau and Schelp2] and independently Thomason [Reference Thomason3] proved that
![]() $(2^k+o(1))n\le r(B_n^{(k)},B_n^{(k)})\le 4^kn.$
In particular, Rousseau and Sheehan [Reference Rousseau and Sheehan4] showed that
$(2^k+o(1))n\le r(B_n^{(k)},B_n^{(k)})\le 4^kn.$
In particular, Rousseau and Sheehan [Reference Rousseau and Sheehan4] showed that
![]() $r(B_n,B_n)=4n+2$
if
$r(B_n,B_n)=4n+2$
if
![]() $4n+1$
is a prime power. Recently, a breakthrough result of Conlon [Reference Conlon5] established that for each
$4n+1$
is a prime power. Recently, a breakthrough result of Conlon [Reference Conlon5] established that for each
![]() $k\ge 2$
,
$k\ge 2$
,
which confirms a conjecture of Thomason [Reference Thomason3] asymptotically and also gives an answer to a problem proposed by Erdős, Faudree, Rousseau and Schelp [Reference Erdős, Faudree, Rousseau and Schelp2]. The error term
![]() $o(n)$
of the upper bound has been improved to
$o(n)$
of the upper bound has been improved to
![]() $O\big (\frac{n}{(\log \log \log n)^{1/25}}\big )$
by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6] using a different method, in particular avoiding the use of the full regularity lemma.
$O\big (\frac{n}{(\log \log \log n)^{1/25}}\big )$
by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6] using a different method, in particular avoiding the use of the full regularity lemma.
For the off-diagonal Ramsey number of books, a simple lower bound is as follows: for any
![]() $k,m,n\in \mathbb{N}$
with
$k,m,n\in \mathbb{N}$
with
![]() $m\le n$
,
$m\le n$
,
Indeed, this follows from an observation of Chvátal and Harary [Reference Chvátal and Harary7] which states that if
![]() $H$
is connected, then
$H$
is connected, then
![]() $r(G,H)\ge (\chi (G)-1)(|V(H)|-1)+1$
. We say that
$r(G,H)\ge (\chi (G)-1)(|V(H)|-1)+1$
. We say that
![]() $H$
is
$H$
is
![]() $G$
-good if this inequality is tight. Burr and Erdős [Reference Burr and Erdös8] initiated the study of such Ramsey goodness problems; the reader is referred to the survey of Conlon, Fox, and Sudakov [Reference Conlon, Fox and Sudakov9] for a detailed history of the area. Among these results, Nikiforov and Rousseau [Reference Nikiforov and Rousseau10] obtained extremely general results. In particular, they proved the following theorem; see Fox, He and Wigderson [Reference Fox, He and Wigderson11] for a new proof avoiding the application of the regularity lemma.
$G$
-good if this inequality is tight. Burr and Erdős [Reference Burr and Erdös8] initiated the study of such Ramsey goodness problems; the reader is referred to the survey of Conlon, Fox, and Sudakov [Reference Conlon, Fox and Sudakov9] for a detailed history of the area. Among these results, Nikiforov and Rousseau [Reference Nikiforov and Rousseau10] obtained extremely general results. In particular, they proved the following theorem; see Fox, He and Wigderson [Reference Fox, He and Wigderson11] for a new proof avoiding the application of the regularity lemma.
Theorem 1.1 (Nikiforov and Rousseau [Reference Nikiforov and Rousseau10]). For every
![]() $k\ge 2$
, there exists some
$k\ge 2$
, there exists some
![]() $\alpha _0\in (0,1)$
such that, for any
$\alpha _0\in (0,1)$
such that, for any
![]() $0\lt \alpha \le \alpha _0$
and sufficiently large
$0\lt \alpha \le \alpha _0$
and sufficiently large
![]() $n$
,
$n$
,
Since we are concerned with the asymptotic behaviour of the Ramsey number, we always omit the ceiling and floor signs henceforth.
We know that
![]() $\alpha _0$
in Theorem 1.1 is always small. In fact, if
$\alpha _0$
in Theorem 1.1 is always small. In fact, if
![]() $\alpha$
is sufficiently far from
$\alpha$
is sufficiently far from
![]() $0$
, then the situation of the lower bound is much different. As pointed out by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12], we can get a random lower bound for
$0$
, then the situation of the lower bound is much different. As pointed out by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12], we can get a random lower bound for
![]() $r(B_{\alpha n}^{(k)},B_n^{(k)})$
as follows (one can also see [Reference Chen, Lin and You13] for the special case of
$r(B_{\alpha n}^{(k)},B_n^{(k)})$
as follows (one can also see [Reference Chen, Lin and You13] for the special case of
![]() $k=2$
). Indeed, for any
$k=2$
). Indeed, for any
![]() $k\in \mathbb{N}$
and
$k\in \mathbb{N}$
and
![]() $0\lt \alpha \le 1$
, let
$0\lt \alpha \le 1$
, let
![]() $p=\frac 1{\alpha ^{1/k}+1}$
and
$p=\frac 1{\alpha ^{1/k}+1}$
and
![]() $N=(p^{-k}-o(1))n$
. Then we randomly and independently colour every edge of
$N=(p^{-k}-o(1))n$
. Then we randomly and independently colour every edge of
![]() $K_N$
blue with probability
$K_N$
blue with probability
![]() $p$
and red with probability
$p$
and red with probability
![]() $1-p$
. A standard application of the Chernoff bound yields that the probability containing a blue
$1-p$
. A standard application of the Chernoff bound yields that the probability containing a blue
![]() $B_n^{(k)}$
or a red
$B_n^{(k)}$
or a red
![]() $B_{\alpha n}^{(k)}$
is
$B_{\alpha n}^{(k)}$
is
![]() $o(1)$
. Therefore, for any
$o(1)$
. Therefore, for any
![]() $k\in \mathbb{N}$
and
$k\in \mathbb{N}$
and
![]() $0\lt \alpha \le 1$
,
$0\lt \alpha \le 1$
,
A simple calculation implies that for large
![]() $k$
, if
$k$
, if
![]() $\alpha \gt ((1+o(1))\frac{\log k}k)^k$
, then the above lower bound is much larger than that of (1), where the logarithm is to base
$\alpha \gt ((1+o(1))\frac{\log k}k)^k$
, then the above lower bound is much larger than that of (1), where the logarithm is to base
![]() $e$
.
$e$
.
Furthermore, Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12] show that the random lower bound becomes asymptotically tight at this point.
Theorem 1.2 (Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12]). For every
![]() $k\ge 2$
, there exists some
$k\ge 2$
, there exists some
![]() $\alpha _1=\alpha _1(k)\in (0,1]$
such that, for any fixed
$\alpha _1=\alpha _1(k)\in (0,1]$
such that, for any fixed
![]() $\alpha _1\le \alpha \le 1$
,
$\alpha _1\le \alpha \le 1$
,
Moreover, one may take
![]() $\alpha _1(k)=((1+o(1))\frac{\log k}k)^k$
.
$\alpha _1(k)=((1+o(1))\frac{\log k}k)^k$
.
From Theorem 1.1 and Theorem 1.2, we know that for every
![]() $k\ge 2$
, there exist
$k\ge 2$
, there exist
![]() $\alpha _0,\alpha _1\in (0,1]$
such that the following holds:
$\alpha _0,\alpha _1\in (0,1]$
such that the following holds:
-
(i) if
 $0\lt \alpha \le \alpha _0$
, then
$0\lt \alpha \le \alpha _0$
, then
 $r(B_{\alpha n}^{(k)},B_n^{(k)})= k(n+k-1)+1$
;
$r(B_{\alpha n}^{(k)},B_n^{(k)})= k(n+k-1)+1$
; -
(ii) if
 $\alpha _1\le \alpha \le 1$
, then
$\alpha _1\le \alpha \le 1$
, then
 $r(B_{\alpha n}^{(k)},B_n^{(k)})= (\alpha ^{1/k}+1)^kn+o(n).$
$r(B_{\alpha n}^{(k)},B_n^{(k)})= (\alpha ^{1/k}+1)^kn+o(n).$
However, the values of
![]() $\alpha _0$
and
$\alpha _0$
and
![]() $\alpha _1$
are not very clear in general. Moreover, although Theorem 1.2 shows that the random lower bound becomes asymptotically tight when
$\alpha _1$
are not very clear in general. Moreover, although Theorem 1.2 shows that the random lower bound becomes asymptotically tight when
![]() $k\to \infty$
, it does not say anything non-trivial in the simplest case
$k\to \infty$
, it does not say anything non-trivial in the simplest case
![]() $k=2$
except when
$k=2$
except when
![]() $\alpha =1$
.
$\alpha =1$
.
Nikiforov and Rousseau [Reference Nikiforov and Rousseau14] proved that
which implies the Ramsey goodness of large books. Moreover, the constant
![]() $1/6$
is asymptotically best possible, i.e., for any
$1/6$
is asymptotically best possible, i.e., for any
![]() $\alpha \gt 1/6$
and all large
$\alpha \gt 1/6$
and all large
![]() $n$
,
$n$
,
Recently, the second author together with Chen and You [Reference Chen, Lin and You13] proved that for all large
![]() $m\le n$
,
$m\le n$
,
![]() $r(B_m, B_n)\le 2(m+n)+o(n).$
However, the behaviour of
$r(B_m, B_n)\le 2(m+n)+o(n).$
However, the behaviour of
![]() $r(B_{\alpha n},B_n)$
is still not well-understood for
$r(B_{\alpha n},B_n)$
is still not well-understood for
![]() $1/6\le \alpha \lt 1$
.
$1/6\le \alpha \lt 1$
.
More recently, Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12, Conjecture 6.1] proposed the following conjecture, which would imply that the random lower bound
![]() $r(B_{\alpha n},B_n)\ge (\sqrt{\alpha }+1)^2n-o(n)$
is not tight for any
$r(B_{\alpha n},B_n)\ge (\sqrt{\alpha }+1)^2n-o(n)$
is not tight for any
![]() $\alpha \lt 1$
.
$\alpha \lt 1$
.
Conjecture 1.3 (Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12]). For every
![]() $\alpha \lt 1$
, the random lower bound for
$\alpha \lt 1$
, the random lower bound for
![]() $r(B_{\alpha n},B_n)$
is not tight. In other words, there exists some
$r(B_{\alpha n},B_n)$
is not tight. In other words, there exists some
![]() $\beta \gt (\sqrt{\alpha }+1)^2$
such that
$\beta \gt (\sqrt{\alpha }+1)^2$
such that
![]() $r(B_{\alpha n},B_n)\ge \beta n$
for all
$r(B_{\alpha n},B_n)\ge \beta n$
for all
![]() $n$
sufficiently large.
$n$
sufficiently large.
Note that Conjecture 1.3 holds for any
![]() $\alpha \le 1/6$
, by (2). However, in this paper, we disprove Conjecture 1.3 by showing that the random lower bound is asymptotically tight for any
$\alpha \le 1/6$
, by (2). However, in this paper, we disprove Conjecture 1.3 by showing that the random lower bound is asymptotically tight for any
![]() $1/4\leq \alpha \leq 1$
.
$1/4\leq \alpha \leq 1$
.
Theorem 1.4.
For any fixed
![]() $1/4\leq \alpha \leq 1$
and sufficiently large
$1/4\leq \alpha \leq 1$
and sufficiently large
![]() $n$
,
$n$
,
Moreover, we give an upper bound of
![]() $r(B_{\alpha n}, B_n)$
for
$r(B_{\alpha n}, B_n)$
for
![]() $1/6\leq \alpha \le 1/4$
.
$1/6\leq \alpha \le 1/4$
.
Theorem 1.5.
For any fixed
![]() $1/6\leq \alpha \le 1/4$
and sufficiently large
$1/6\leq \alpha \le 1/4$
and sufficiently large
![]() $n$
,
$n$
,
The inequality is asymptotically tight when
![]() $\alpha =1/6$
or
$\alpha =1/6$
or
![]() $1/4$
.
$1/4$
.
We also have the following lower bound.
Theorem 1.6.
Let
![]() $1/6\le \alpha \le \frac{52-16\sqrt{3}}{121}\approx 0.2007$
be fixed, and let
$1/6\le \alpha \le \frac{52-16\sqrt{3}}{121}\approx 0.2007$
be fixed, and let
![]() $p=\frac{1-\sqrt{\alpha (3-2\alpha )}}{1-2\alpha }$
. Then for all sufficiently large
$p=\frac{1-\sqrt{\alpha (3-2\alpha )}}{1-2\alpha }$
. Then for all sufficiently large
![]() $n$
,
$n$
,
The inequality is asymptotically tight when
![]() $\alpha =1/6$
.
$\alpha =1/6$
.
Remark 1.7. Since
![]() $\frac{3}{1+2p^2}\gt (\sqrt{\alpha }+1)^2$
for any
$\frac{3}{1+2p^2}\gt (\sqrt{\alpha }+1)^2$
for any
![]() $1/6\le \alpha \lt \frac{52-16\sqrt{3}}{121}$
, we have that Conjecture 1.3 holds in this interval.
$1/6\le \alpha \lt \frac{52-16\sqrt{3}}{121}$
, we have that Conjecture 1.3 holds in this interval.
1.1. Notation
For a book
![]() $B_n$
, we refer to the common edge as the base of the book
$B_n$
, we refer to the common edge as the base of the book
![]() $B_n$
. For a graph
$B_n$
. For a graph
![]() $G=(V,E)$
with vertex set
$G=(V,E)$
with vertex set
![]() $V$
and edge set
$V$
and edge set
![]() $E$
, we write
$E$
, we write
![]() $bk_G$
for the size of the largest book in a graph
$bk_G$
for the size of the largest book in a graph
![]() $G$
. Let
$G$
. Let
![]() $uv$
denote an edge of
$uv$
denote an edge of
![]() $G$
. For
$G$
. For
![]() $X \subseteq V$
,
$X \subseteq V$
,
![]() $e(X)$
is the number of edges in
$e(X)$
is the number of edges in
![]() $X$
. For two disjoint subsets
$X$
. For two disjoint subsets
![]() $X,Y\subseteq V$
,
$X,Y\subseteq V$
,
![]() $e_G(X,Y)$
denotes the number of edges between
$e_G(X,Y)$
denotes the number of edges between
![]() $X$
and
$X$
and
![]() $Y$
. The neighbourhood of a vertex
$Y$
. The neighbourhood of a vertex
![]() $v$
in
$v$
in
![]() $U\subseteq V$
is denoted by
$U\subseteq V$
is denoted by
![]() $N_G(v,U)$
, and
$N_G(v,U)$
, and
![]() $\deg _G(v,U)=|N_G(v,U)|$
and the degree of
$\deg _G(v,U)=|N_G(v,U)|$
and the degree of
![]() $v$
in
$v$
in
![]() $G$
is
$G$
is
![]() $\deg _G(v)=|N_G(v,V)|$
. Let
$\deg _G(v)=|N_G(v,V)|$
. Let
![]() $X \sqcup Y$
denote the disjoint union of
$X \sqcup Y$
denote the disjoint union of
![]() $X$
and
$X$
and
![]() $Y$
. Let
$Y$
. Let
![]() $[n]=\{1,2,\dots,n\}$
, and
$[n]=\{1,2,\dots,n\}$
, and
![]() $[m,n]=\{m,m+1,\dots,n\}$
. We always delete the subscriptions if there is no confusion from the context.
$[m,n]=\{m,m+1,\dots,n\}$
. We always delete the subscriptions if there is no confusion from the context.
The rest of the paper is organised as follows. In Section 2, we will collect several useful lemmas. In Sections 3 and 4, we shall present the proofs of Theorems 1.4, 1.5 and 1.6. Finally, we will have some discussion in Section 5.
2. Preliminaries
The proofs rely on the regularity method [Reference Szemerédi15], which is a powerful tool in extremal graph theory. There are many important applications of the regularity lemma, and we refer the reader to the nice surveys [Reference Komlós, Shokoufandeh, Simonovits and Szemerédi16–Reference Rödl and Schacht18] and many other recent references.
Let
![]() $G=(V,E)$
be a graph. For two vertex sets
$G=(V,E)$
be a graph. For two vertex sets
![]() $A,B\subseteq V(G)$
, we call
$A,B\subseteq V(G)$
, we call
![]() $d(A,B)=\frac{e(A,B)}{|A||B|}$
the density of the pair
$d(A,B)=\frac{e(A,B)}{|A||B|}$
the density of the pair
![]() $(A,B)$
. Let
$(A,B)$
. Let
![]() $\varepsilon \gt 0$
, a pair
$\varepsilon \gt 0$
, a pair
![]() $(A,B)$
is said to be
$(A,B)$
is said to be
![]() $\varepsilon$
-regular if
$\varepsilon$
-regular if
![]() $|d(A,B)-d(X,Y)|\le \varepsilon$
for every
$|d(A,B)-d(X,Y)|\le \varepsilon$
for every
![]() $X\subseteq A$
,
$X\subseteq A$
,
![]() $Y\subseteq B$
with
$Y\subseteq B$
with
![]() $|X|\ge \varepsilon |A|$
and
$|X|\ge \varepsilon |A|$
and
![]() $|Y|\ge \varepsilon |B|$
. Also, a subset
$|Y|\ge \varepsilon |B|$
. Also, a subset
![]() $A$
is said to be
$A$
is said to be
![]() $\varepsilon$
-regular if the pair
$\varepsilon$
-regular if the pair
![]() $(A,A)$
is
$(A,A)$
is
![]() $\varepsilon$
-regular.
$\varepsilon$
-regular.
Given a graph
![]() $G$
, an equitable
$G$
, an equitable
![]() $\varepsilon$
-regular partition
$\varepsilon$
-regular partition
![]() $V(G)=\sqcup _{i=1}^k V_i$
of
$V(G)=\sqcup _{i=1}^k V_i$
of
![]() $G$
is a partition of
$G$
is a partition of
![]() $V(G)$
such that (i)
$V(G)$
such that (i)
![]() $||V_i|-|V_j||\le 1$
for all distinct
$||V_i|-|V_j||\le 1$
for all distinct
![]() $i$
and
$i$
and
![]() $j$
; (ii) each
$j$
; (ii) each
![]() $V_{i}$
is
$V_{i}$
is
![]() $\varepsilon$
-regular; and (iii) for every
$\varepsilon$
-regular; and (iii) for every
![]() $1\le i\le k$
, there are at most
$1\le i\le k$
, there are at most
![]() $\varepsilon k$
values
$\varepsilon k$
values
![]() $1\le j\le k$
such that the pair
$1\le j\le k$
such that the pair
![]() $(V_i, V_j)$
is not
$(V_i, V_j)$
is not
![]() $\varepsilon$
-regular.
$\varepsilon$
-regular.
When establishing the asymptotic order of
![]() $r(B^{(k)}_n,B^{(k)}_n)$
, Conlon [Reference Conlon5, Lemma 3] applied a refined version of the regularity lemma which guarantees a regular subset in each part of the partition for any graph. We will use the following refined regularity lemma due to Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6, Lemma 2.1], which is a strengthening of that due to Conlon [Reference Conlon5] and the usual version of Szemerédi’s regularity lemma [Reference Szemerédi15].
$r(B^{(k)}_n,B^{(k)}_n)$
, Conlon [Reference Conlon5, Lemma 3] applied a refined version of the regularity lemma which guarantees a regular subset in each part of the partition for any graph. We will use the following refined regularity lemma due to Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6, Lemma 2.1], which is a strengthening of that due to Conlon [Reference Conlon5] and the usual version of Szemerédi’s regularity lemma [Reference Szemerédi15].
Lemma 2.1 (Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6]).For every
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $M_0\in \mathbb{N}$
, there is some
$M_0\in \mathbb{N}$
, there is some
![]() $M=M(\varepsilon, M_0)\gt M_0$
such that for every graph
$M=M(\varepsilon, M_0)\gt M_0$
such that for every graph
![]() $G$
, there is an equitable
$G$
, there is an equitable
![]() $\varepsilon$
-regular partition
$\varepsilon$
-regular partition
![]() $V(G)=\sqcup _{i=1}^k V_i$
where
$V(G)=\sqcup _{i=1}^k V_i$
where
![]() $M_0\le k\le M$
.
$M_0\le k\le M$
.
We will use the following version of the counting lemma, proved by Conlon [Reference Conlon5, Lemma 5]. (A similar counting lemma was proved by Nikiforov and Rousseau [Reference Nikiforov and Rousseau14, Corollary 11], but they required all of the clusters to be different.) For the general local counting lemma, see Rödl and Schacht [Reference Rödl and Schacht18, Theorem 18].
Lemma 2.2 (Conlon [Reference Conlon5]). For any
![]() $\delta \gt 0$
, there is
$\delta \gt 0$
, there is
![]() $\varepsilon \gt 0$
such that if
$\varepsilon \gt 0$
such that if
![]() $U_{1},U_{2}$
(not necessarily distinct),
$U_{1},U_{2}$
(not necessarily distinct),
![]() $W_{1},\ldots,W_{l}$
are vertex sets with
$W_{1},\ldots,W_{l}$
are vertex sets with
![]() $(U_{1},U_{2})$
$(U_{1},U_{2})$
![]() $\varepsilon$
-regular of density at least
$\varepsilon$
-regular of density at least
![]() $\delta$
and
$\delta$
and
![]() $(U_{i},W_{j})$
$(U_{i},W_{j})$
![]() $\varepsilon$
-regular of density
$\varepsilon$
-regular of density
![]() $d_{ij}$
for all
$d_{ij}$
for all
![]() $i\in [2]$
and
$i\in [2]$
and
![]() $j\in [l]$
, then there exists an edge
$j\in [l]$
, then there exists an edge
![]() $u_1 u_2$
where
$u_1 u_2$
where
![]() $u_1\in U_1$
and
$u_1\in U_1$
and
![]() $u_2\in U_2$
such that
$u_2\in U_2$
such that
![]() $u_1$
and
$u_1$
and
![]() $u_2$
have at least
$u_2$
have at least
![]() $\sum ^{l}_{j=1}(d_{1j}d_{2j}-\delta )|W_{j}|$
common neighbours in
$\sum ^{l}_{j=1}(d_{1j}d_{2j}-\delta )|W_{j}|$
common neighbours in
![]() $\sqcup _{j=1}^l W_j$
.
$\sqcup _{j=1}^l W_j$
.
We will also use the following well-known Turán’s bound.
Lemma 2.3 (Turán [Reference Turán19]). For any graph
![]() $G$
of order
$G$
of order
![]() $n$
with average degree
$n$
with average degree
![]() $d$
, the independence number
$d$
, the independence number
![]() $\alpha (G)$
is at least
$\alpha (G)$
is at least
![]() $\frac{n}{1+d}.$
$\frac{n}{1+d}.$
3. Proofs of Theorem 1.4 and Theorem 1.5
In the following, for a red/blue edge colouring of
![]() $K_N$
, we always use
$K_N$
, we always use
![]() $R/B$
to denote the subgraph induced by all red/blue edges. For every
$R/B$
to denote the subgraph induced by all red/blue edges. For every
![]() $i,j, (i \neq j$
), let
$i,j, (i \neq j$
), let
![]() $d_{ij}$
be the red density of the pair
$d_{ij}$
be the red density of the pair
![]() $(V_i, V_j)$
, i.e.,
$(V_i, V_j)$
, i.e.,
![]() $d_{ij}=\frac{e_R(V_i, V_j)}{|V_i||V_j|}$
.
$d_{ij}=\frac{e_R(V_i, V_j)}{|V_i||V_j|}$
.
We will use the following definition introduced by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12].
Definition 3.1. Fix parameters
![]() $\ell \in \mathbb{N}$
and
$\ell \in \mathbb{N}$
and
![]() $\varepsilon,\gamma \in (0,1)$
and suppose that we are given a red/blue colouring of
$\varepsilon,\gamma \in (0,1)$
and suppose that we are given a red/blue colouring of
![]() $E(K_N)$
. Then an
$E(K_N)$
. Then an
![]() $\ell$
-tuple of pairwise disjoint vertex sets
$\ell$
-tuple of pairwise disjoint vertex sets
![]() $V_1,\ldots, V_\ell \subseteq V(K_N)$
is called an
$V_1,\ldots, V_\ell \subseteq V(K_N)$
is called an
![]() $(\ell,\varepsilon,\gamma )$
-red-blocked configuration if the following properties are satisfied:
$(\ell,\varepsilon,\gamma )$
-red-blocked configuration if the following properties are satisfied:
-
1. Each
 $V_i$
is
$V_i$
is
 $\varepsilon$
-regular with itself,
$\varepsilon$
-regular with itself, -
2. Each
 $V_i$
has internal red density at least
$V_i$
has internal red density at least
 $\gamma$
, and
$\gamma$
, and -
3. For all
 $i\neq j$
, the pair
$i\neq j$
, the pair
 $(V_i,V_j)$
is
$(V_i,V_j)$
is
 $\varepsilon$
-regular and has blue density at least
$\varepsilon$
-regular and has blue density at least
 $\gamma$
.
$\gamma$
.
Similarly, we say that
![]() $V_1,\ldots, V_\ell$
is an
$V_1,\ldots, V_\ell$
is an
![]() $(\ell,\varepsilon,\gamma )$
-blue-blocked configuration if properties (1–3) hold, but the roles of red and blue interchanged.
$(\ell,\varepsilon,\gamma )$
-blue-blocked configuration if properties (1–3) hold, but the roles of red and blue interchanged.
We first have a specific structure as in the following lemma, where the proof relies on the refined regularity lemma due to Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6] together with the idea from Nikiforov and Rousseau [Reference Nikiforov and Rousseau14].
Lemma 3.2.
Let
![]() $1/6\leq \alpha \leq 1$
,
$1/6\leq \alpha \leq 1$
,
![]() $\varepsilon,\gamma \in (0,1)$
where
$\varepsilon,\gamma \in (0,1)$
where
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\gamma$
, and
$\gamma$
, and
![]() $n$
is a large integer. Consider a red/blue edge colouring of
$n$
is a large integer. Consider a red/blue edge colouring of
![]() $K_N$
and an equitable
$K_N$
and an equitable
![]() $\varepsilon$
-regular partition of
$\varepsilon$
-regular partition of
![]() $V(R)$
guaranteed by Lemma 2.1 with
$V(R)$
guaranteed by Lemma 2.1 with
![]() $N=(x+y\alpha )n+o(n)$
, where
$N=(x+y\alpha )n+o(n)$
, where
![]() $x+y=xy$
,
$x+y=xy$
,
![]() $1\leq x\leq y\leq 2x$
. If
$1\leq x\leq y\leq 2x$
. If
![]() $R$
is
$R$
is
![]() $B_n$
-free and
$B_n$
-free and
![]() $B$
is
$B$
is
![]() $B_{\alpha n}$
-free, then the following two properties hold:
$B_{\alpha n}$
-free, then the following two properties hold:
-
(1) there exists no
 $(3,\varepsilon,\gamma )$
-red-blocked configuration;
$(3,\varepsilon,\gamma )$
-red-blocked configuration;
-
(2) there exists no
 $(2,\varepsilon,\gamma )$
-blue-blocked configuration.
$(2,\varepsilon,\gamma )$
-blue-blocked configuration.
Proof. Let
![]() $N=(x+y\alpha +\eta )n$
where
$N=(x+y\alpha +\eta )n$
where
![]() $\eta \gt 0$
is sufficiently small. Consider a red/blue edge colouring of
$\eta \gt 0$
is sufficiently small. Consider a red/blue edge colouring of
![]() $K_N$
on vertex set
$K_N$
on vertex set
![]() $[N]$
. We assume that
$[N]$
. We assume that
![]() $\gamma \gt 0$
is taken sufficiently small in terms of
$\gamma \gt 0$
is taken sufficiently small in terms of
![]() $\eta$
. Set
$\eta$
. Set
![]() $\delta =\gamma ^2/2$
. Note that
$\delta =\gamma ^2/2$
. Note that
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\delta$
, since
$\delta$
, since
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\gamma$
.
$\gamma$
.
By Lemma 2.1, there is an equitable
![]() $\varepsilon$
-regular partition
$\varepsilon$
-regular partition
![]() $[N]=\sqcup _{i=1}^k V_i$
for the red graph
$[N]=\sqcup _{i=1}^k V_i$
for the red graph
![]() $R$
, i.e., (i)
$R$
, i.e., (i)
![]() $||V_i|-|V_j||\le 1$
for all distinct
$||V_i|-|V_j||\le 1$
for all distinct
![]() $i$
and
$i$
and
![]() $j$
; (ii) each part
$j$
; (ii) each part
![]() $V_{i}$
is
$V_{i}$
is
![]() $\varepsilon$
-regular; and (iii) for every
$\varepsilon$
-regular; and (iii) for every
![]() $1\le i\le k$
, there are at most
$1\le i\le k$
, there are at most
![]() $\varepsilon k$
values
$\varepsilon k$
values
![]() $1\le j\le k$
such that the pair
$1\le j\le k$
such that the pair
![]() $(V_i, V_j)$
is not
$(V_i, V_j)$
is not
![]() $\varepsilon$
-regular. Because the colours are complementary, the same conclusion holds for the blue graph. For convenience, we may assume
$\varepsilon$
-regular. Because the colours are complementary, the same conclusion holds for the blue graph. For convenience, we may assume
![]() $|V_i|=N/k\,{=:}\,t$
for all
$|V_i|=N/k\,{=:}\,t$
for all
![]() $i\in [k]$
. By the assumption that
$i\in [k]$
. By the assumption that
![]() $R$
is
$R$
is
![]() $B_n$
-free and
$B_n$
-free and
![]() $B$
is
$B$
is
![]() $B_{\alpha n}$
-free, we have
$B_{\alpha n}$
-free, we have
Now we shall prove that there exists no
![]() $(3,\varepsilon,\gamma )$
-red-blocked configuration. On the contrary, we may assume that
$(3,\varepsilon,\gamma )$
-red-blocked configuration. On the contrary, we may assume that
![]() $V_1,V_2,V_3$
is a
$V_1,V_2,V_3$
is a
![]() $(3,\varepsilon,\gamma )$
-red-blocked configuration. Let
$(3,\varepsilon,\gamma )$
-red-blocked configuration. Let
![]() $M$
be the set of all
$M$
be the set of all
![]() $s\in [k]\setminus [3]$
such that every pair
$s\in [k]\setminus [3]$
such that every pair
![]() $(V_i,V_s)$
for
$(V_i,V_s)$
for
![]() $i\in [3]$
is
$i\in [3]$
is
![]() $\varepsilon$
-regular; clearly,
$\varepsilon$
-regular; clearly,
![]() $|M|\ge (k-3)-3\varepsilon k\geq (1-4\varepsilon )k$
.
$|M|\ge (k-3)-3\varepsilon k\geq (1-4\varepsilon )k$
.
We compute the maximum size of the red books with bases in
![]() $E(V_i)$
for
$E(V_i)$
for
![]() $i\in [3]$
. Since the red density of the pair
$i\in [3]$
. Since the red density of the pair
![]() $(V_i,V_s)$
is
$(V_i,V_s)$
is
![]() $d_{is}$
, we apply Lemma 2.2 to obtain that
$d_{is}$
, we apply Lemma 2.2 to obtain that
On the other hand, applying Lemma 2.2, we obtain that the maximum size
![]() $S$
of the blue books with bases in
$S$
of the blue books with bases in
![]() $E(V_1,V_2)$
satisfies
$E(V_1,V_2)$
satisfies
Considering in turn
![]() $(V_1,V_3)$
and
$(V_1,V_3)$
and
![]() $(V_2,V_3)$
, we obtain exactly in the same way,
$(V_2,V_3)$
, we obtain exactly in the same way,
Let
 \begin{equation*}d_s=\sum _{i=1}^3d_{is},\;\;\text {and} \;\;d_0=\frac {1}{|M|}\sum \limits _{s\in M}d_s.\end{equation*}
\begin{equation*}d_s=\sum _{i=1}^3d_{is},\;\;\text {and} \;\;d_0=\frac {1}{|M|}\sum \limits _{s\in M}d_s.\end{equation*}
Adding (6), (7), and (8) each multiplied by
![]() $y/3$
together with (5) for each
$y/3$
together with (5) for each
![]() $i\in [3]$
multiplied by
$i\in [3]$
multiplied by
![]() $x/3$
, noting
$x/3$
, noting
![]() $2x\ge y$
, and applying Cauchy’s inequality to the double sum we obtain
$2x\ge y$
, and applying Cauchy’s inequality to the double sum we obtain
 \begin{align*} y\cdot bk_B+x\cdot bk_R \geq & \frac{y}{3}\sum \limits _{s\in M}\left (3-2d_s+\sum \limits _{1\le i\lt j\le 3}d_{is}d_{js}-3\delta \right )t+\frac{x}{3}\sum _{s\in M}\left (\sum _{i=1}^3d_{is}^2-3\delta \right )t \\[3pt] \ge & \sum _{s\in M}\left (\frac{y}{3}\left (3-2d_s+\frac{d_s^2}{2}-\frac{1}{2}\sum _{i=1}^3d_{is}^2\right ) +\frac{x}{3}\sum _{i=1}^3d_{is}^2\right )t-(x+y)\delta kt \\[3pt] \geq & \sum _{s\in M}\left (\frac{y}{3}\left (3-2d_s+\frac{d_s^2}{2}\right )+\left (\frac{x}{3}-\frac y6\right )\cdot \frac 13{d_s^2}\right )t-(x+y)\delta kt \\[3pt] =&\sum _{s\in M}\left (\frac{y}{3}\left (3-2d_s\right )+\frac{x+y}{9}{d_s^2}\right )t-(x+y)\delta kt \\[3pt] \geq & |M|\left (\frac{y}{3}\left (3-2d_0\right )+\frac{x+y}{9}{d_0^2}\right )t-(x+y)\delta kt. \end{align*}
\begin{align*} y\cdot bk_B+x\cdot bk_R \geq & \frac{y}{3}\sum \limits _{s\in M}\left (3-2d_s+\sum \limits _{1\le i\lt j\le 3}d_{is}d_{js}-3\delta \right )t+\frac{x}{3}\sum _{s\in M}\left (\sum _{i=1}^3d_{is}^2-3\delta \right )t \\[3pt] \ge & \sum _{s\in M}\left (\frac{y}{3}\left (3-2d_s+\frac{d_s^2}{2}-\frac{1}{2}\sum _{i=1}^3d_{is}^2\right ) +\frac{x}{3}\sum _{i=1}^3d_{is}^2\right )t-(x+y)\delta kt \\[3pt] \geq & \sum _{s\in M}\left (\frac{y}{3}\left (3-2d_s+\frac{d_s^2}{2}\right )+\left (\frac{x}{3}-\frac y6\right )\cdot \frac 13{d_s^2}\right )t-(x+y)\delta kt \\[3pt] =&\sum _{s\in M}\left (\frac{y}{3}\left (3-2d_s\right )+\frac{x+y}{9}{d_s^2}\right )t-(x+y)\delta kt \\[3pt] \geq & |M|\left (\frac{y}{3}\left (3-2d_0\right )+\frac{x+y}{9}{d_0^2}\right )t-(x+y)\delta kt. \end{align*}
Therefore, from (3) and (4), we obtain that
Since
![]() $|M|\geq (1-4\varepsilon )k$
, we have
$|M|\geq (1-4\varepsilon )k$
, we have
Thus, by noting
![]() $\delta =\gamma ^2/2$
,
$\delta =\gamma ^2/2$
,
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\gamma$
, we have
$\gamma$
, we have
This leads to a contradiction since the right-hand side is negative for sufficiently small
![]() $\gamma$
and the left-hand side is non-negative for
$\gamma$
and the left-hand side is non-negative for
![]() $\frac{x+y}{9}\gt 0$
and the discriminant of the quadratic form
$\frac{x+y}{9}\gt 0$
and the discriminant of the quadratic form
![]() $\Delta =(\frac{2y}{3})^2-\frac{4(x+y)(y-1)}{9}=\frac 49({-}xy+x+y)=0$
since
$\Delta =(\frac{2y}{3})^2-\frac{4(x+y)(y-1)}{9}=\frac 49({-}xy+x+y)=0$
since
![]() $x+y=xy$
.
$x+y=xy$
.
It remains to prove that there exists no
![]() $(2,\varepsilon,\gamma )$
-blue-blocked configuration. On the contrary, suppose that
$(2,\varepsilon,\gamma )$
-blue-blocked configuration. On the contrary, suppose that
![]() $V_1,V_2$
is a
$V_1,V_2$
is a
![]() $(2,\varepsilon,\gamma )$
-blue-blocked configuration without loss of generality. Let
$(2,\varepsilon,\gamma )$
-blue-blocked configuration without loss of generality. Let
![]() $M$
be the set of all
$M$
be the set of all
![]() $s\in [k]\setminus [2]$
such that all pairs
$s\in [k]\setminus [2]$
such that all pairs
![]() $(V_1, V_s)$
and
$(V_1, V_s)$
and
![]() $(V_2, V_s)$
are
$(V_2, V_s)$
are
![]() $\varepsilon$
-regular; clearly
$\varepsilon$
-regular; clearly
![]() $|M|\ge (k-2)-2\varepsilon k\geq (1-3\varepsilon )k$
.
$|M|\ge (k-2)-2\varepsilon k\geq (1-3\varepsilon )k$
.
By a similar argument as aforementioned, we obtain that for
![]() $i\in [2]$
,
$i\in [2]$
,
Similarly,
Let
![]() $d_s=\sum _{i=1}^2 d_{is}$
, and
$d_s=\sum _{i=1}^2 d_{is}$
, and
![]() $d_0=\frac{1}{|M|}\sum _{s\in M}d_s.$
Adding (10) multiplied by
$d_0=\frac{1}{|M|}\sum _{s\in M}d_s.$
Adding (10) multiplied by
![]() $x$
together with (9) for each
$x$
together with (9) for each
![]() $i\in [2]$
multiplied by
$i\in [2]$
multiplied by
![]() $y/2$
, noting
$y/2$
, noting
![]() $x\le y$
, and applying Cauchy’s inequality to the double sum we obtain
$x\le y$
, and applying Cauchy’s inequality to the double sum we obtain
 \begin{align*} y\cdot bk_B+x\cdot bk_R \geq & \frac y2\sum _{s\in M}\left (2-2d_s+\sum _{i=1}^2 d_{is}^2-2\delta \right )t+x\sum _{s\in M}\left (d_{1s}d_{2s}-\delta \right )t \\\ge & \sum _{s\in M}\left (\frac y2(2-2d_s)+\frac{y}{2}\sum _{i=1}^2 d_{is}^2+\frac x2\left (d_s^2-\sum _{i=1}^2 d_{is}^2\right )\right )t-(x+y)\delta kt \\ \geq & \sum _{s\in M}\left (\frac y2(2-2d_s)+\frac{y+x}{2}\cdot \frac{d_s^2}{2}\right )t-(x+y)\delta kt \\ \geq & |M|\left (\frac y2(2-2d_0)+\frac{y+x}{4}d_0^2\right )t-(x+y)\delta kt. \end{align*}
\begin{align*} y\cdot bk_B+x\cdot bk_R \geq & \frac y2\sum _{s\in M}\left (2-2d_s+\sum _{i=1}^2 d_{is}^2-2\delta \right )t+x\sum _{s\in M}\left (d_{1s}d_{2s}-\delta \right )t \\\ge & \sum _{s\in M}\left (\frac y2(2-2d_s)+\frac{y}{2}\sum _{i=1}^2 d_{is}^2+\frac x2\left (d_s^2-\sum _{i=1}^2 d_{is}^2\right )\right )t-(x+y)\delta kt \\ \geq & \sum _{s\in M}\left (\frac y2(2-2d_s)+\frac{y+x}{2}\cdot \frac{d_s^2}{2}\right )t-(x+y)\delta kt \\ \geq & |M|\left (\frac y2(2-2d_0)+\frac{y+x}{4}d_0^2\right )t-(x+y)\delta kt. \end{align*}
Therefore, from (3) and (4), we obtain that
Since
![]() $|M|\geq (1-3\varepsilon )k$
, we have
$|M|\geq (1-3\varepsilon )k$
, we have
Thus, by noting
![]() $\delta =\gamma ^2/2$
,
$\delta =\gamma ^2/2$
,
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\gamma$
, we have that
$\gamma$
, we have that
This leads to a contradiction since the right-hand side is negative for sufficiently small
![]() $\gamma$
and the left-hand side is non-negative for
$\gamma$
and the left-hand side is non-negative for
![]() $\frac{y+x}{4}\gt 0$
and the discriminant of the quadratic form
$\frac{y+x}{4}\gt 0$
and the discriminant of the quadratic form
![]() $\Delta =y^2-(y+x)(y-1)=-xy+x+y=0$
. This completes the proof of Lemma 3.2.
$\Delta =y^2-(y+x)(y-1)=-xy+x+y=0$
. This completes the proof of Lemma 3.2.
Now, we are ready to give proofs for Theorem 1.4 and Theorem 1.5.
Proof sketches of Theorem 1.4 and Theorem 1.5. Consider a red/blue edge colouring of
![]() $K_N$
for some suitable
$K_N$
for some suitable
![]() $N$
. On the contrary, we suppose that
$N$
. On the contrary, we suppose that
![]() $bk_R\lt n$
and
$bk_R\lt n$
and
![]() $bk_B\lt \alpha n$
. Firstly, we apply the refined regularity lemma due to Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6] to obtain an equitable
$bk_B\lt \alpha n$
. Firstly, we apply the refined regularity lemma due to Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6] to obtain an equitable
![]() $\varepsilon$
-regular partition of
$\varepsilon$
-regular partition of
![]() $V(R)$
which guarantees the regularity of each cluster with itself. Secondly, from the assumption that
$V(R)$
which guarantees the regularity of each cluster with itself. Secondly, from the assumption that
![]() $bk_R\lt n$
and
$bk_R\lt n$
and
![]() $bk_B\lt \alpha n$
, Lemma 3.2 implies that there are no
$bk_B\lt \alpha n$
, Lemma 3.2 implies that there are no
![]() $(3,\varepsilon,\gamma )$
-red-blocked and
$(3,\varepsilon,\gamma )$
-red-blocked and
![]() $(2,\varepsilon,\gamma )$
-blue-blocked configurations, which are the bases for subsequent calculations of the corresponding book sizes. According to the densities of clusters, we partition these clusters into red clusters and blue clusters. For Theorem 1.4, applying the counting lemma due to Conlon [Reference Conlon5] to a single red/blue cluster, and combining with Turán’s bound on the subgraph
$(2,\varepsilon,\gamma )$
-blue-blocked configurations, which are the bases for subsequent calculations of the corresponding book sizes. According to the densities of clusters, we partition these clusters into red clusters and blue clusters. For Theorem 1.4, applying the counting lemma due to Conlon [Reference Conlon5] to a single red/blue cluster, and combining with Turán’s bound on the subgraph
![]() $H$
defined on the red clusters, we finally obtain
$H$
defined on the red clusters, we finally obtain
![]() $2bk_R+bk_B\ge 2n + \alpha n$
, which leads to a contradiction. For Theorem 1.5, based on the lower bounds of the book sizes of
$2bk_R+bk_B\ge 2n + \alpha n$
, which leads to a contradiction. For Theorem 1.5, based on the lower bounds of the book sizes of
![]() $R/B$
, we need to consider the total blue/red densities between red-cluster sets and blue-cluster sets. The situation is more complicated and the computation is much more technical.
$R/B$
, we need to consider the total blue/red densities between red-cluster sets and blue-cluster sets. The situation is more complicated and the computation is much more technical.
The reason we have some improvements is that the specific structure, i.e., there exists no
![]() $(3,\varepsilon,\gamma )$
-red-blocked and
$(3,\varepsilon,\gamma )$
-red-blocked and
![]() $(2,\varepsilon,\gamma )$
-blue-blocked configurations, is more in line with the essence for 2-books than the structure that no
$(2,\varepsilon,\gamma )$
-blue-blocked configurations, is more in line with the essence for 2-books than the structure that no
![]() $(2,\varepsilon,\gamma )$
-red-blocked and
$(2,\varepsilon,\gamma )$
-red-blocked and
![]() $(2,\varepsilon,\gamma )$
-blue-blocked configurations used by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12]. In particular, the refined regularity lemma by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6] is a key ingredient of the proofs.
$(2,\varepsilon,\gamma )$
-blue-blocked configurations used by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12]. In particular, the refined regularity lemma by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson6] is a key ingredient of the proofs.
Proof of Theorem
1.4. Let
![]() $1/4\leq \alpha \leq 1$
be fixed, and
$1/4\leq \alpha \leq 1$
be fixed, and
![]() $\eta \gt 0$
is sufficiently small and
$\eta \gt 0$
is sufficiently small and
![]() $n$
is sufficiently large. Let
$n$
is sufficiently large. Let
![]() $N=(x+y\alpha +\eta )n$
where
$N=(x+y\alpha +\eta )n$
where
![]() $x+y=xy$
,
$x+y=xy$
,
![]() $1\leq x\leq y\leq 2x$
. Consider a red/blue edge colouring of
$1\leq x\leq y\leq 2x$
. Consider a red/blue edge colouring of
![]() $K_N$
on vertex set
$K_N$
on vertex set
![]() $[N]$
. Let
$[N]$
. Let
![]() $\gamma \gt 0$
be sufficiently small in terms of
$\gamma \gt 0$
be sufficiently small in terms of
![]() $\eta$
. Set
$\eta$
. Set
![]() $\delta =\gamma ^2/2$
. We assume that
$\delta =\gamma ^2/2$
. We assume that
![]() $\varepsilon \gt 0$
is sufficiently small in terms of
$\varepsilon \gt 0$
is sufficiently small in terms of
![]() $\delta$
and
$\delta$
and
![]() $\gamma$
.
$\gamma$
.
By Lemma 2.1, there is an equitable
![]() $\varepsilon$
-regular partition
$\varepsilon$
-regular partition
![]() $[N]=\sqcup _{i=1}^k V_i$
for the red graph
$[N]=\sqcup _{i=1}^k V_i$
for the red graph
![]() $R$
, i.e., (i)
$R$
, i.e., (i)
![]() $||V_i|-|V_j||\le 1$
for all distinct
$||V_i|-|V_j||\le 1$
for all distinct
![]() $i$
and
$i$
and
![]() $j$
; (ii) each part
$j$
; (ii) each part
![]() $V_{i}$
is
$V_{i}$
is
![]() $\varepsilon$
-regular; and (iii) for every
$\varepsilon$
-regular; and (iii) for every
![]() $1\le i\le k$
, there are at most
$1\le i\le k$
, there are at most
![]() $\varepsilon k$
values
$\varepsilon k$
values
![]() $1\le j\le k$
such that the pair
$1\le j\le k$
such that the pair
![]() $(V_i, V_j)$
is not
$(V_i, V_j)$
is not
![]() $\varepsilon$
-regular. Because the colours are complementary, the same conclusion holds for the blue graph. For convenience, we may assume
$\varepsilon$
-regular. Because the colours are complementary, the same conclusion holds for the blue graph. For convenience, we may assume
![]() $|V_i|=N/k\,{=:}\,t$
for all
$|V_i|=N/k\,{=:}\,t$
for all
![]() $i\in [k]$
. It suffices to show that for all sufficiently large
$i\in [k]$
. It suffices to show that for all sufficiently large
![]() $n$
, there exists a red
$n$
, there exists a red
![]() $B_n$
or a blue
$B_n$
or a blue
![]() $B_{\alpha n}$
. On the contrary,
$B_{\alpha n}$
. On the contrary,
We call a cluster
![]() $V_{i}$
red if at least half of its internal edges are red and blue otherwise. Clearly, every cluster is either red or blue.
$V_{i}$
red if at least half of its internal edges are red and blue otherwise. Clearly, every cluster is either red or blue.
Now we assume that
![]() $V_1,\ldots, V_l$
are blue clusters without loss of generality and set
$V_1,\ldots, V_l$
are blue clusters without loss of generality and set
![]() $l=\lambda k$
,
$l=\lambda k$
,
![]() $0\le \lambda \le 1$
. To finish the proof, we will show that (11) or (12) is not true.
$0\le \lambda \le 1$
. To finish the proof, we will show that (11) or (12) is not true.
We first fix a blue cluster
![]() $V_i$
and compute the maximum size of the blue books whose bases lie in
$V_i$
and compute the maximum size of the blue books whose bases lie in
![]() $E(V_i)$
. Let
$E(V_i)$
. Let
![]() $M_i$
be the set of all
$M_i$
be the set of all
![]() $s\in [k]\setminus \{i\}$
such that
$s\in [k]\setminus \{i\}$
such that
![]() $(V_i, V_s)$
is an
$(V_i, V_s)$
is an
![]() $\varepsilon$
-regular pair, and let
$\varepsilon$
-regular pair, and let
![]() $M_{i1} =M_i\cap [l].$
Clearly,
$M_{i1} =M_i\cap [l].$
Clearly,
![]() $l\ge |M_{i1}|\ge l-1-\varepsilon k\ge (\lambda -2\varepsilon )k$
since
$l\ge |M_{i1}|\ge l-1-\varepsilon k\ge (\lambda -2\varepsilon )k$
since
![]() $|M_i|\ge (1-\varepsilon )k$
.
$|M_i|\ge (1-\varepsilon )k$
.
By Lemma 3.2 (2), for every
![]() $s\in M_{i1}$
, the red density
$s\in M_{i1}$
, the red density
![]() $d_{is}$
of the pair
$d_{is}$
of the pair
![]() $(V_i, V_s)$
satisfies
$(V_i, V_s)$
satisfies
![]() $d_{is}\le \gamma$
, so the blue density of
$d_{is}\le \gamma$
, so the blue density of
![]() $(V_i, V_s)$
is at least
$(V_i, V_s)$
is at least
![]() $1-\gamma$
. Therefore, by Lemma 2.2 and noting
$1-\gamma$
. Therefore, by Lemma 2.2 and noting
![]() $\delta =\gamma ^2/2$
, the maximum size
$\delta =\gamma ^2/2$
, the maximum size
![]() $S$
of the blue books whose bases are in
$S$
of the blue books whose bases are in
![]() $E(V_i)$
satisfies
$E(V_i)$
satisfies
Then, by noting
![]() $|M_{i1}|\ge (\lambda -2\varepsilon )k$
, we find that
$|M_{i1}|\ge (\lambda -2\varepsilon )k$
, we find that
Next we consider the maximum size of the red books whose bases are contained in a red cluster. Let us define the graph
![]() $H$
as follows. The vertex set of
$H$
as follows. The vertex set of
![]() $H$
is
$H$
is
![]() $[l+1,k]$
and two vertices
$[l+1,k]$
and two vertices
![]() $i,j\in [l+1,k]$
are joined if and only if the red density
$i,j\in [l+1,k]$
are joined if and only if the red density
![]() $d_{ij}$
of the
$d_{ij}$
of the
![]() $\varepsilon$
-regular pair
$\varepsilon$
-regular pair
![]() $(V_i, V_j)$
satisfies
$(V_i, V_j)$
satisfies
![]() $d_{ij}\gt 1-\gamma .$
$d_{ij}\gt 1-\gamma .$
By Lemma 3.2 (1), the complement of
![]() $H$
is triangle-free, i.e., the independence number of
$H$
is triangle-free, i.e., the independence number of
![]() $H$
is at most two, hence Lemma 2.3 implies that the average degree of
$H$
is at most two, hence Lemma 2.3 implies that the average degree of
![]() $H$
is at least
$H$
is at least
![]() $(k-l)/2-1$
. So there exists a vertex
$(k-l)/2-1$
. So there exists a vertex
![]() $i\in [l+1,k]$
such that the degree of
$i\in [l+1,k]$
such that the degree of
![]() $i$
in
$i$
in
![]() $H$
is at least
$H$
is at least
![]() $(k-l)/2-1$
. Let
$(k-l)/2-1$
. Let
![]() $N_i$
be the set of all
$N_i$
be the set of all
![]() $s\in [k]\setminus \{i\}$
such that
$s\in [k]\setminus \{i\}$
such that
![]() $(V_i, V_s)$
is an
$(V_i, V_s)$
is an
![]() $\varepsilon$
-regular pair, and let
$\varepsilon$
-regular pair, and let
![]() $ N_{i1}=N_i\cap N_H(i).$
Clearly,
$ N_{i1}=N_i\cap N_H(i).$
Clearly,
![]() $k-l\ge |N_{i1}|\ge (k-l)/2-1-\varepsilon k$
since
$k-l\ge |N_{i1}|\ge (k-l)/2-1-\varepsilon k$
since
![]() $|N_i|\geq (1-\varepsilon )k$
.
$|N_i|\geq (1-\varepsilon )k$
.
By Lemma 2.2 and
![]() $\delta =\gamma ^2/2$
, the maximum size
$\delta =\gamma ^2/2$
, the maximum size
![]() $S$
of the red books whose bases lie in
$S$
of the red books whose bases lie in
![]() $E(V_i)$
satisfies
$E(V_i)$
satisfies
Then, by noting
![]() $|N_{i1}|\ge (k-l)/2-1-\varepsilon k\geq \left (\frac{1-\lambda }{2}-2\varepsilon \right )k$
, we find that
$|N_{i1}|\ge (k-l)/2-1-\varepsilon k\geq \left (\frac{1-\lambda }{2}-2\varepsilon \right )k$
, we find that
Adding (13) and (14) multiplied by
![]() $2$
, we obtain
$2$
, we obtain
To prove Theorem 1.4, we take
![]() $x=\sqrt{\alpha }+1$
,
$x=\sqrt{\alpha }+1$
,
![]() $y=1+\frac{1}{\sqrt{\alpha }}$
. Since
$y=1+\frac{1}{\sqrt{\alpha }}$
. Since
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\gamma$
and
$\gamma$
and
![]() $\frac{2+\alpha }{x+y\alpha }\leq 1$
for
$\frac{2+\alpha }{x+y\alpha }\leq 1$
for
![]() $\frac 14\leq \alpha \leq 1$
, we have
$\frac 14\leq \alpha \leq 1$
, we have
It follows that either
![]() $2bk_R\geq (\frac{2}{x+y\alpha }-2\gamma ) kt$
, or
$2bk_R\geq (\frac{2}{x+y\alpha }-2\gamma ) kt$
, or
![]() $bk_B\geq (\frac{\alpha }{x+y\alpha }-\alpha \gamma ) kt,$
which contradicts (11) or (12), respectively. The proof of Theorem 1.4 is complete.
$bk_B\geq (\frac{\alpha }{x+y\alpha }-\alpha \gamma ) kt,$
which contradicts (11) or (12), respectively. The proof of Theorem 1.4 is complete.
Proof of Theorem
1.5. Let
![]() $1/6\leq \alpha \leq 1/4$
be fixed, and
$1/6\leq \alpha \leq 1/4$
be fixed, and
![]() $\eta \gt 0$
is sufficiently small and
$\eta \gt 0$
is sufficiently small and
![]() $n$
is sufficiently large. Let
$n$
is sufficiently large. Let
![]() $N=(x+y\alpha +\eta )n$
, where
$N=(x+y\alpha +\eta )n$
, where
![]() $x=3/2$
and
$x=3/2$
and
![]() $y=3$
, so
$y=3$
, so
![]() $x+y=xy$
. Consider a red/blue edge colouring of
$x+y=xy$
. Consider a red/blue edge colouring of
![]() $K_N$
on vertex set
$K_N$
on vertex set
![]() $[N]$
. Let
$[N]$
. Let
![]() $\gamma \gt 0$
be sufficiently small in terms of
$\gamma \gt 0$
be sufficiently small in terms of
![]() $\eta$
. Set
$\eta$
. Set
![]() $\delta =\gamma ^2/2$
, and
$\delta =\gamma ^2/2$
, and
![]() $\varepsilon \gt 0$
is taken sufficiently small in terms of
$\varepsilon \gt 0$
is taken sufficiently small in terms of
![]() $\delta$
and
$\delta$
and
![]() $\gamma$
.
$\gamma$
.
Similarly, by Lemma 2.1, there is an equitable
![]() $\varepsilon$
-regular partition
$\varepsilon$
-regular partition
![]() $[N]=\sqcup _{i=1}^k V_i$
for the red graph
$[N]=\sqcup _{i=1}^k V_i$
for the red graph
![]() $R$
. For convenience, we may assume
$R$
. For convenience, we may assume
![]() $|V_i|=N/k\,{=:}\,t$
for all
$|V_i|=N/k\,{=:}\,t$
for all
![]() $i\in [k]$
. It suffices to show that for all sufficiently large
$i\in [k]$
. It suffices to show that for all sufficiently large
![]() $n$
, there exists a red
$n$
, there exists a red
![]() $B_n$
or a blue
$B_n$
or a blue
![]() $B_{\alpha n}$
. On the contrary,
$B_{\alpha n}$
. On the contrary,
We call a cluster
![]() $V_{i}$
red if at least half of its internal edges are red and blue otherwise. Clearly, every cluster is either red or blue. Now we assume that
$V_{i}$
red if at least half of its internal edges are red and blue otherwise. Clearly, every cluster is either red or blue. Now we assume that
![]() $V_1,\ldots, V_l$
are blue clusters without loss of generality and set
$V_1,\ldots, V_l$
are blue clusters without loss of generality and set
![]() $l=\lambda k$
,
$l=\lambda k$
,
![]() $0\le \lambda \le 1$
. We first consider a blue cluster
$0\le \lambda \le 1$
. We first consider a blue cluster
![]() $V_i$
and compute the maximum size of the blue books whose bases lie in
$V_i$
and compute the maximum size of the blue books whose bases lie in
![]() $E(V_i)$
. Let
$E(V_i)$
. Let
![]() $M_i$
be the set of all
$M_i$
be the set of all
![]() $s\in [k]\setminus \{i\}$
such that
$s\in [k]\setminus \{i\}$
such that
![]() $(V_i, V_s)$
is an
$(V_i, V_s)$
is an
![]() $\varepsilon$
-regular pair, and let
$\varepsilon$
-regular pair, and let
Clearly,
![]() $l\ge |M_{i1}|\ge l-1-\varepsilon k\geq (\lambda -2\varepsilon ) k$
since
$l\ge |M_{i1}|\ge l-1-\varepsilon k\geq (\lambda -2\varepsilon ) k$
since
![]() $|M_i|\ge (1-\varepsilon )k$
.
$|M_i|\ge (1-\varepsilon )k$
.
By Lemma 3.2 (2), for every
![]() $s\in M_{i1}$
, the red density
$s\in M_{i1}$
, the red density
![]() $d_{is}$
of the pair
$d_{is}$
of the pair
![]() $(V_i, V_s)$
satisfies
$(V_i, V_s)$
satisfies
![]() $d_{is}\le \gamma$
, so the blue density of
$d_{is}\le \gamma$
, so the blue density of
![]() $(V_i, V_s)$
is at least
$(V_i, V_s)$
is at least
![]() $1-\gamma$
. Therefore, by Lemma 2.2 and noting
$1-\gamma$
. Therefore, by Lemma 2.2 and noting
![]() $\delta =\gamma ^2/2$
, the maximum size
$\delta =\gamma ^2/2$
, the maximum size
![]() $S$
of the blue books whose bases are in
$S$
of the blue books whose bases are in
![]() $E(V_i)$
satisfies
$E(V_i)$
satisfies
 \begin{align*} S&\ge \sum _{s\in M_{i1}}\left ((1-\gamma )^2-\delta \right )t+\sum _{s\in M_{i2}}((1-d_{is})^2-\delta )t\\&\ge (1-2\gamma ) |M_{i1}|t+\sum _{s\in M_{i2}}(1-d_{is})^2 t -\delta |M_{i2}|t. \end{align*}
\begin{align*} S&\ge \sum _{s\in M_{i1}}\left ((1-\gamma )^2-\delta \right )t+\sum _{s\in M_{i2}}((1-d_{is})^2-\delta )t\\&\ge (1-2\gamma ) |M_{i1}|t+\sum _{s\in M_{i2}}(1-d_{is})^2 t -\delta |M_{i2}|t. \end{align*}
Then, by noting
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\delta$
,
$\delta$
,
![]() $|M_{i1}|\ge (\lambda -2\varepsilon )k$
and
$|M_{i1}|\ge (\lambda -2\varepsilon )k$
and
![]() $|M_{i2}|\leq k$
, and applying Cauchy’s inequality, we obtain
$|M_{i2}|\leq k$
, and applying Cauchy’s inequality, we obtain
 \begin{align*} bk_B\ge S \ge & (1-2\gamma )(\lambda -2\varepsilon )kt+\sum _{s\in M_{i2}}(1-d_{is})^2 t -\delta kt \\ \geq & (1-2\gamma )\lambda kt+\frac{1}{|M_{i2}|}\left (\sum _{s\in M_{i2}}(1-d_{is})\right )^2 t -2\delta kt. \end{align*}
\begin{align*} bk_B\ge S \ge & (1-2\gamma )(\lambda -2\varepsilon )kt+\sum _{s\in M_{i2}}(1-d_{is})^2 t -\delta kt \\ \geq & (1-2\gamma )\lambda kt+\frac{1}{|M_{i2}|}\left (\sum _{s\in M_{i2}}(1-d_{is})\right )^2 t -2\delta kt. \end{align*}
Recall (16) and
![]() $\delta =\gamma ^2/2$
, we obtain that
$\delta =\gamma ^2/2$
, we obtain that
 \begin{align} \frac{1}{|M_{i2}|}\left (\sum _{s\in M_{i2}}(1-d_{is})\right )^2 t \lt \left (\frac{\alpha }{x+y\alpha }-20\gamma -(1-2\gamma )\lambda +2\delta \right )kt \leq \left (\frac{\alpha }{x+y\alpha }-\lambda -15\gamma \right )kt. \end{align}
\begin{align} \frac{1}{|M_{i2}|}\left (\sum _{s\in M_{i2}}(1-d_{is})\right )^2 t \lt \left (\frac{\alpha }{x+y\alpha }-20\gamma -(1-2\gamma )\lambda +2\delta \right )kt \leq \left (\frac{\alpha }{x+y\alpha }-\lambda -15\gamma \right )kt. \end{align}
We may assume
![]() $\lambda \leq \frac{\alpha }{x+y\alpha }\lt 1/2$
, otherwise the right-hand side of (17) is negative, which is not possible since the left-hand side is non-negative. Since
$\lambda \leq \frac{\alpha }{x+y\alpha }\lt 1/2$
, otherwise the right-hand side of (17) is negative, which is not possible since the left-hand side is non-negative. Since
![]() $|M_{i2}|\leq k-l=(1-\lambda )k$
, we have
$|M_{i2}|\leq k-l=(1-\lambda )k$
, we have
 \begin{equation*} \sum _{s\in M_{i2}}(1-d_{is}) \lt k\sqrt {\left (\frac {\alpha }{x+y\alpha }-\lambda -15\gamma \right )(1-\lambda )}. \end{equation*}
\begin{equation*} \sum _{s\in M_{i2}}(1-d_{is}) \lt k\sqrt {\left (\frac {\alpha }{x+y\alpha }-\lambda -15\gamma \right )(1-\lambda )}. \end{equation*}
Summing over all
![]() $i\in [l]$
and noting that
$i\in [l]$
and noting that
![]() $l=\lambda k\lt k/2$
, we obtain that the total blue densities of all regular pairs
$l=\lambda k\lt k/2$
, we obtain that the total blue densities of all regular pairs
![]() $(V_i,V_s)$
where
$(V_i,V_s)$
where
![]() $i\in [l]$
and
$i\in [l]$
and
![]() $s\in [l+1,k]$
satisfies that
$s\in [l+1,k]$
satisfies that
 \begin{align} \sum _{i=1}^l \sum _{s\in M_{i2}}(1-d_{is}) \lt \lambda k^2\sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda -15\gamma \right )(1-\lambda )}. \end{align}
\begin{align} \sum _{i=1}^l \sum _{s\in M_{i2}}(1-d_{is}) \lt \lambda k^2\sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda -15\gamma \right )(1-\lambda )}. \end{align}
Next we consider the maximum size of the red books whose bases are contained in a red cluster. Let us define the graph
![]() $H$
as follows. The vertices of
$H$
as follows. The vertices of
![]() $H$
are the numbers
$H$
are the numbers
![]() $[l+1,k]$
and two vertices
$[l+1,k]$
and two vertices
![]() $i,j$
are joined if and only if the red density
$i,j$
are joined if and only if the red density
![]() $d_{ij}$
of the
$d_{ij}$
of the
![]() $\varepsilon$
-regular pair
$\varepsilon$
-regular pair
![]() $(V_i, V_j)$
satisfies
$(V_i, V_j)$
satisfies
![]() $d_{ij}\gt 1-\gamma .$
$d_{ij}\gt 1-\gamma .$
By Lemma 3.2 (1), the complement of
![]() $H$
is triangle-free, hence Lemma 2.3 implies that the average degree of
$H$
is triangle-free, hence Lemma 2.3 implies that the average degree of
![]() $H$
is at least
$H$
is at least
![]() $(k-l)/2-1$
. Thus, recall
$(k-l)/2-1$
. Thus, recall
![]() $l\leq k/2$
, if
$l\leq k/2$
, if
![]() $k$
is sufficiently large, then
$k$
is sufficiently large, then
For any
![]() $i\in [l+1,k]$
, let
$i\in [l+1,k]$
, let
![]() $N_i$
be the set of all
$N_i$
be the set of all
![]() $s\in [k]\setminus \{i\}$
such that
$s\in [k]\setminus \{i\}$
such that
![]() $(V_i, V_s)$
is
$(V_i, V_s)$
is
![]() $\varepsilon$
-regular, and let
$\varepsilon$
-regular, and let
Since
![]() $|N_i|\ge (1-\varepsilon )k$
, we have
$|N_i|\ge (1-\varepsilon )k$
, we have
![]() $ \deg _H(i)\ge |N_{i1}|\ge \deg _H(i)-\varepsilon k.$
Therefore, since
$ \deg _H(i)\ge |N_{i1}|\ge \deg _H(i)-\varepsilon k.$
Therefore, since
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\delta$
, the maximum size
$\delta$
, the maximum size
![]() $S_i$
of the red books whose bases lie in
$S_i$
of the red books whose bases lie in
![]() $E(V_i)$
satisfies
$E(V_i)$
satisfies
 \begin{align*} S_i\ge & \sum _{s\in N_{i1}}\left ((1-\gamma )^2-\delta \right )t+\sum _{s\in N_{i2}}(d_{is}^2-\delta )t \\ \ge & (1-2\gamma )|N_{i1}|t+\sum _{s\in N_{i2}}d_{is}^2 t-\delta |N_{i2}|t \\ \ge & (1-2\gamma )\deg _H(i)t+\sum _{s\in N_{i2}}d_{is}^2 t-2\delta kt. \end{align*}
\begin{align*} S_i\ge & \sum _{s\in N_{i1}}\left ((1-\gamma )^2-\delta \right )t+\sum _{s\in N_{i2}}(d_{is}^2-\delta )t \\ \ge & (1-2\gamma )|N_{i1}|t+\sum _{s\in N_{i2}}d_{is}^2 t-\delta |N_{i2}|t \\ \ge & (1-2\gamma )\deg _H(i)t+\sum _{s\in N_{i2}}d_{is}^2 t-2\delta kt. \end{align*}
It follows that
 \begin{align*} \sum _{i=l+1}^k S_i\ge & \sum _{i=l+1}^k (1-2\gamma )\deg _H(i)t+\sum _{i=l+1}^k \sum _{s\in N_{i2}}d_{is}^2 t-2\delta k(k-l)t \\ \geq & (1-2\gamma )2e(H)t+\sum _{i=l+1}^k\sum _{s\in N_{i2}}d_{is}^2 t-2\delta k(k-l)t. \end{align*}
\begin{align*} \sum _{i=l+1}^k S_i\ge & \sum _{i=l+1}^k (1-2\gamma )\deg _H(i)t+\sum _{i=l+1}^k \sum _{s\in N_{i2}}d_{is}^2 t-2\delta k(k-l)t \\ \geq & (1-2\gamma )2e(H)t+\sum _{i=l+1}^k\sum _{s\in N_{i2}}d_{is}^2 t-2\delta k(k-l)t. \end{align*}
Hence by (19) and
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\delta$
, we obtain that
$\delta$
, we obtain that
 \begin{align*} \sum _{i=l+1}^k S_i \ge & (1-2\gamma )(1/2-2\varepsilon )(k-l)^2t+\sum _{i=l+1}^k\sum _{s\in N_{i2}}d_{is}^2 t-2\delta k(k-l)t \\ \ge & \frac{1}{2}(1-2\gamma )(k-l)^2t+\sum _{i=l+1}^k\sum _{s\in N_{i2}}d_{is}^2 t-4\delta k(k-l)t. \end{align*}
\begin{align*} \sum _{i=l+1}^k S_i \ge & (1-2\gamma )(1/2-2\varepsilon )(k-l)^2t+\sum _{i=l+1}^k\sum _{s\in N_{i2}}d_{is}^2 t-2\delta k(k-l)t \\ \ge & \frac{1}{2}(1-2\gamma )(k-l)^2t+\sum _{i=l+1}^k\sum _{s\in N_{i2}}d_{is}^2 t-4\delta k(k-l)t. \end{align*}
Then by noting that
![]() $|N_{i2}|\leq l=\lambda k$
and applying Cauchy’s inequality to the double sum, we have
$|N_{i2}|\leq l=\lambda k$
and applying Cauchy’s inequality to the double sum, we have
 \begin{align*} bk_R\ge \frac{1}{k-l}\sum _{i=l+1}^k S_i\ge &\frac{1}{2}(1-2\gamma )(k-l)t+\frac{1}{k-l}\sum _{i=l+1}^k\sum _{s\in N_{i2}}d_{is}^2 t-4\delta kt \\ \geq &\frac{1}{2}(1-2\gamma )(1-\lambda )kt+ \frac{1}{(k-l)l}\sum _{i=l+1}^k\left (\sum _{s\in N_{i2}}d_{is}\right )^2 t-4\delta kt \\ \geq &\frac{1}{2}(1-2\gamma )(1-\lambda )kt+ \frac{1}{(k-l)^2l}\left (\sum _{i=l+1}^k \sum _{s\in N_{i2}}d_{is}\right )^2 t-4\delta kt. \end{align*}
\begin{align*} bk_R\ge \frac{1}{k-l}\sum _{i=l+1}^k S_i\ge &\frac{1}{2}(1-2\gamma )(k-l)t+\frac{1}{k-l}\sum _{i=l+1}^k\sum _{s\in N_{i2}}d_{is}^2 t-4\delta kt \\ \geq &\frac{1}{2}(1-2\gamma )(1-\lambda )kt+ \frac{1}{(k-l)l}\sum _{i=l+1}^k\left (\sum _{s\in N_{i2}}d_{is}\right )^2 t-4\delta kt \\ \geq &\frac{1}{2}(1-2\gamma )(1-\lambda )kt+ \frac{1}{(k-l)^2l}\left (\sum _{i=l+1}^k \sum _{s\in N_{i2}}d_{is}\right )^2 t-4\delta kt. \end{align*}
So we obtain
Recall (15), we obtain that
 \begin{align*} \frac{1}{(k-l)^2l}\left (\sum _{i=l+1}^k \sum _{s\in N_{i2}}d_{is}\right )^2 t \lt &\left (\frac{1}{x+y\alpha }-\gamma \right )kt-\frac{1}{2}(1-2\gamma )(1-\lambda )kt +4\delta kt \\ \leq & \left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}+4\delta \right )kt. \end{align*}
\begin{align*} \frac{1}{(k-l)^2l}\left (\sum _{i=l+1}^k \sum _{s\in N_{i2}}d_{is}\right )^2 t \lt &\left (\frac{1}{x+y\alpha }-\gamma \right )kt-\frac{1}{2}(1-2\gamma )(1-\lambda )kt +4\delta kt \\ \leq & \left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}+4\delta \right )kt. \end{align*}
Recall
![]() $l=\lambda k$
, we obtain that the total red densities of all regular pairs
$l=\lambda k$
, we obtain that the total red densities of all regular pairs
![]() $(V_i,V_s)$
where
$(V_i,V_s)$
where
![]() $i\in [l+1,k]$
and
$i\in [l+1,k]$
and
![]() $s\in [l]$
satisfies that
$s\in [l]$
satisfies that
 \begin{align} \sum _{i=l+1}^k \sum _{s\in N_{i2}} d_{is} \lt (1-\lambda )k^2\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}+4\delta \right )\lambda }. \end{align}
\begin{align} \sum _{i=l+1}^k \sum _{s\in N_{i2}} d_{is} \lt (1-\lambda )k^2\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}+4\delta \right )\lambda }. \end{align}
Therefore, adding (18) and (21), we obtain
 \begin{align*} \sum _{i=1}^{l}\sum _{s\in M_{i2}}1 &=\sum _{i=1}^l \sum _{s\in M_{i2}}(1-d_{is})+\sum _{i=1}^l \sum _{s\in M_{i2}} d_{is} =\sum _{i=1}^l \sum _{s\in M_{i2}}(1-d_{is})+\sum _{i=l+1}^k \sum _{s\in N_{i2}} d_{is} \\&\lt \lambda k^2\sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda -15\gamma \right )(1-\lambda )}+ (1-\lambda )k^2\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}+4\delta \right )\lambda }. \end{align*}
\begin{align*} \sum _{i=1}^{l}\sum _{s\in M_{i2}}1 &=\sum _{i=1}^l \sum _{s\in M_{i2}}(1-d_{is})+\sum _{i=1}^l \sum _{s\in M_{i2}} d_{is} =\sum _{i=1}^l \sum _{s\in M_{i2}}(1-d_{is})+\sum _{i=l+1}^k \sum _{s\in N_{i2}} d_{is} \\&\lt \lambda k^2\sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda -15\gamma \right )(1-\lambda )}+ (1-\lambda )k^2\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}+4\delta \right )\lambda }. \end{align*}
Note that
![]() $\sum _{i=1}^{l}\sum _{s\in M_{i2}}1\geq (k-l)l-\varepsilon k^2=((1-\lambda )\lambda -\varepsilon )k^2$
, we have
$\sum _{i=1}^{l}\sum _{s\in M_{i2}}1\geq (k-l)l-\varepsilon k^2=((1-\lambda )\lambda -\varepsilon )k^2$
, we have
 \begin{align*} ((1-\lambda )\lambda -\varepsilon )k^2\lt \lambda k^2\sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda -15\gamma \right )(1-\lambda )} +(1-\lambda )k^2\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}+4\delta \right )\lambda }. \end{align*}
\begin{align*} ((1-\lambda )\lambda -\varepsilon )k^2\lt \lambda k^2\sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda -15\gamma \right )(1-\lambda )} +(1-\lambda )k^2\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}+4\delta \right )\lambda }. \end{align*}
Suppose
![]() $\lambda \leq \eta/10$
, then we are done from (20) that
$\lambda \leq \eta/10$
, then we are done from (20) that
by noting
![]() $\alpha \ge 1/6$
, and
$\alpha \ge 1/6$
, and
![]() $\gamma$
and
$\gamma$
and
![]() $\delta$
are sufficiently small in terms of
$\delta$
are sufficiently small in terms of
![]() $\eta$
. Therefore, we may assume
$\eta$
. Therefore, we may assume
![]() $\lambda \gt \eta/10$
.
$\lambda \gt \eta/10$
.
Since
![]() $\gamma$
is sufficiently small in terms of
$\gamma$
is sufficiently small in terms of
![]() $\lambda$
,
$\lambda$
,
![]() $\alpha$
,
$\alpha$
,
![]() $x$
and
$x$
and
![]() $y$
, and
$y$
, and
![]() $\delta =\gamma ^2/2$
, and
$\delta =\gamma ^2/2$
, and
![]() $\varepsilon$
is sufficiently small in terms of
$\varepsilon$
is sufficiently small in terms of
![]() $\gamma$
, we obtain
$\gamma$
, we obtain
 \begin{align*} (1-\lambda )\lambda \lt & \lambda \sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda \right )(1-\lambda )}+(1-\lambda )\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}\right )\lambda }, \end{align*}
\begin{align*} (1-\lambda )\lambda \lt & \lambda \sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda \right )(1-\lambda )}+(1-\lambda )\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}\right )\lambda }, \end{align*}
and consequently,
 \begin{align} \sqrt{(1-\lambda )\lambda }\lt \sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda \right )\lambda } +\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}\right )(1-\lambda )}. \end{align}
\begin{align} \sqrt{(1-\lambda )\lambda }\lt \sqrt{\left (\frac{\alpha }{x+y\alpha }-\lambda \right )\lambda } +\sqrt{\left (\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}\right )(1-\lambda )}. \end{align}
Since (22) makes sense, we obtain
![]() $1-\frac{2}{x+y\alpha }\leq \lambda \leq \frac{\alpha }{x+y\alpha }$
. Recall that
$1-\frac{2}{x+y\alpha }\leq \lambda \leq \frac{\alpha }{x+y\alpha }$
. Recall that
![]() $1/6\leq \alpha \leq 1/4$
,
$1/6\leq \alpha \leq 1/4$
,
![]() $x=3/2$
and
$x=3/2$
and
![]() $y=3$
, so
$y=3$
, so
![]() $\frac{\alpha +{11}/{6}}{x+y\alpha }\leq 1$
, implying
$\frac{\alpha +{11}/{6}}{x+y\alpha }\leq 1$
, implying
![]() $\frac{\alpha }{x+y\alpha } \leq \frac{1}{12}+\frac{11}{12}(1-\frac{2}{x+y\alpha }) \leq \frac{1}{12}+\frac{11}{12}\lambda = \frac{1}{12}(1-\lambda )+\lambda .$
Thus
$\frac{\alpha }{x+y\alpha } \leq \frac{1}{12}+\frac{11}{12}(1-\frac{2}{x+y\alpha }) \leq \frac{1}{12}+\frac{11}{12}\lambda = \frac{1}{12}(1-\lambda )+\lambda .$
Thus
![]() $\frac{\alpha }{x+y\alpha }-\lambda \leq \frac{1}{12}(1-\lambda )$
, and so
$\frac{\alpha }{x+y\alpha }-\lambda \leq \frac{1}{12}(1-\lambda )$
, and so
![]() $\sqrt{(\frac{\alpha }{x+y\alpha }-\lambda )\lambda }\le \frac{1}{2\sqrt{3}}\sqrt{(1-\lambda )\lambda }$
.
$\sqrt{(\frac{\alpha }{x+y\alpha }-\lambda )\lambda }\le \frac{1}{2\sqrt{3}}\sqrt{(1-\lambda )\lambda }$
.
Moreover, since
![]() $\frac{1}{2}-\frac{1}{x+y\alpha }\ge 0$
, we obtain that
$\frac{1}{2}-\frac{1}{x+y\alpha }\ge 0$
, we obtain that
 \begin{equation*}\frac {1}{x+y\alpha }-\frac {1}{2} \leq \left (2\left (1-\frac {1}{2\sqrt {3}}\right )^2-1\right )\left (\frac {1}{2}-\frac {1}{x+y\alpha }\right ) \leq \left (\left (1-\frac {1}{2\sqrt {3}}\right )^2-\frac 12\right )\lambda .\end{equation*}
\begin{equation*}\frac {1}{x+y\alpha }-\frac {1}{2} \leq \left (2\left (1-\frac {1}{2\sqrt {3}}\right )^2-1\right )\left (\frac {1}{2}-\frac {1}{x+y\alpha }\right ) \leq \left (\left (1-\frac {1}{2\sqrt {3}}\right )^2-\frac 12\right )\lambda .\end{equation*}
Thus
![]() $\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}\leq (1-\frac{1}{2\sqrt{3}})^2\lambda$
, and so
$\frac{1}{x+y\alpha }-\frac{1-\lambda }{2}\leq (1-\frac{1}{2\sqrt{3}})^2\lambda$
, and so
![]() $\sqrt{(\frac{1}{x+y\alpha }-\frac{1-\lambda }{2})(1-\lambda )}\le (1-\frac{1}{2\sqrt{3}})\sqrt{(1-\lambda )\lambda }$
.
$\sqrt{(\frac{1}{x+y\alpha }-\frac{1-\lambda }{2})(1-\lambda )}\le (1-\frac{1}{2\sqrt{3}})\sqrt{(1-\lambda )\lambda }$
.
Therefore, adding these two terms, the right-hand side of (22) is at most
![]() $\sqrt{(1-\lambda )\lambda }$
, which leads to a contradiction. The proof of Theorem 1.5 is complete.
$\sqrt{(1-\lambda )\lambda }$
, which leads to a contradiction. The proof of Theorem 1.5 is complete.
4. Proof of Theorem 1.6
Let
![]() $\frac 16\le \alpha \le \frac{52-16\sqrt{3}}{121}$
be fixed, and
$\frac 16\le \alpha \le \frac{52-16\sqrt{3}}{121}$
be fixed, and
![]() $p=\frac{1-\sqrt{\alpha (3-2\alpha )}}{1-2\alpha }$
, and
$p=\frac{1-\sqrt{\alpha (3-2\alpha )}}{1-2\alpha }$
, and
![]() $N=(\frac{3}{1+2p^2}-\eta )n$
, where
$N=(\frac{3}{1+2p^2}-\eta )n$
, where
![]() $\eta \gt 0$
is sufficiently small and
$\eta \gt 0$
is sufficiently small and
![]() $n$
is sufficiently large. We shall show that for sufficiently large
$n$
is sufficiently large. We shall show that for sufficiently large
![]() $N$
there exists a partially random red/blue colouring of the edges of
$N$
there exists a partially random red/blue colouring of the edges of
![]() $K_{N}$
for which
$K_{N}$
for which
For convenience, assume that
![]() $N$
is divisible by 3. Partition
$N$
is divisible by 3. Partition
![]() $[N]$
into three sets
$[N]$
into three sets
![]() $A_{1},A_{2},A_{3}$
, each with
$A_{1},A_{2},A_{3}$
, each with
![]() $N/3$
vertices, and colour the graphs induced by
$N/3$
vertices, and colour the graphs induced by
![]() $A_{1},A_{2},A_{3}$
in red. Then edges of the form
$A_{1},A_{2},A_{3}$
in red. Then edges of the form
![]() $uv$
where
$uv$
where
![]() $u\in A_i,v\in A_{j}$
$u\in A_i,v\in A_{j}$
![]() $(1\le i\lt j\le 3)$
are independently coloured red with probability
$(1\le i\lt j\le 3)$
are independently coloured red with probability
![]() $p$
and blue with probability
$p$
and blue with probability
![]() $1-p$
. For
$1-p$
. For
![]() $u,v\in A_{i}$
, the size of the red book with base
$u,v\in A_{i}$
, the size of the red book with base
![]() $uv$
is a random variable with expected value
$uv$
is a random variable with expected value
Now suppose
![]() $u\in A_{i}$
and
$u\in A_{i}$
and
![]() $v\in A_{j}$
where
$v\in A_{j}$
where
![]() $i\neq j$
. If
$i\neq j$
. If
![]() $uv$
is a blue edge, the size of the blue book with base
$uv$
is a blue edge, the size of the blue book with base
![]() $uv$
is a random variable with expected value
$uv$
is a random variable with expected value
by noting that
![]() $\alpha =\frac{(1-p)^2}{1+2p^2}$
.
$\alpha =\frac{(1-p)^2}{1+2p^2}$
.
By noting (23), if
![]() $uv$
is a red edge, then the size of the red book with base
$uv$
is a red edge, then the size of the red book with base
![]() $uv$
is a random variable with expected value
$uv$
is a random variable with expected value
We will use the following version of the Chernoff bound [Reference Janson, Łuczak and Rucinski20, Corollary 2.4 and Theorem 2.8]: let
![]() $X_1, \ldots, X_t$
be independent random variables taking values in {0,1} and let
$X_1, \ldots, X_t$
be independent random variables taking values in {0,1} and let
![]() $X=\sum _{i=1}^t X_i$
. If
$X=\sum _{i=1}^t X_i$
. If
![]() $x\geq c\mathbb{E}(X)$
for some
$x\geq c\mathbb{E}(X)$
for some
![]() $c\gt 1$
, then
$c\gt 1$
, then
![]() $\mathrm{Pr}(X\geq x)\leq e^{-c'x}$
, where
$\mathrm{Pr}(X\geq x)\leq e^{-c'x}$
, where
![]() $c'=\ln c-1+\frac 1c$
.
$c'=\ln c-1+\frac 1c$
.
Plugging in
![]() $c=1/(1-\frac{(1+2p^2)\eta }{3})$
, since
$c=1/(1-\frac{(1+2p^2)\eta }{3})$
, since
![]() $y=\ln x-1+\frac 1x$
is increasing when
$y=\ln x-1+\frac 1x$
is increasing when
![]() $x\geq 1$
, we find that
$x\geq 1$
, we find that
![]() $c'\gt 0$
. Since
$c'\gt 0$
. Since
![]() $\mathrm{Pr}(X_1\geq n)\leq e^{-c'n}$
and
$\mathrm{Pr}(X_1\geq n)\leq e^{-c'n}$
and
![]() $\mathrm{Pr}(X_2\geq \alpha n)\leq e^{-c'\alpha n}$
, where
$\mathrm{Pr}(X_2\geq \alpha n)\leq e^{-c'\alpha n}$
, where
![]() $X_1$
denotes the size of a red book and
$X_1$
denotes the size of a red book and
![]() $X_2$
denotes the size of a blue book, applying a union bound over all edges, we obtain that the probability that there is a red book
$X_2$
denotes the size of a blue book, applying a union bound over all edges, we obtain that the probability that there is a red book
![]() $B_n$
or a blue book
$B_n$
or a blue book
![]() $B_{\alpha n}$
tends to 0 as
$B_{\alpha n}$
tends to 0 as
![]() $n\to \infty$
. Thus for large enough
$n\to \infty$
. Thus for large enough
![]() $N$
the desired red/blue colouring of the edges of
$N$
the desired red/blue colouring of the edges of
![]() $K_{N}$
exists.
$K_{N}$
exists.
5. Concluding remarks
From the result of Nikiforov and Rousseau [Reference Nikiforov and Rousseau14], we know the exact value of
![]() $r(B_{\alpha n}, B_n)$
for
$r(B_{\alpha n}, B_n)$
for
![]() $0\lt \alpha \lt 1/6$
; and from Theorem 1.4, we know the asymptotic behaviour of
$0\lt \alpha \lt 1/6$
; and from Theorem 1.4, we know the asymptotic behaviour of
![]() $r(B_{\alpha n}, B_n)$
for
$r(B_{\alpha n}, B_n)$
for
![]() $1/4\le \alpha \le 1$
, i.e., the random lower bound
$1/4\le \alpha \le 1$
, i.e., the random lower bound
![]() $r(B_{\alpha n},B_n)\ge (\sqrt{\alpha }+1)^2n+o(n)$
is asymptotically tight for
$r(B_{\alpha n},B_n)\ge (\sqrt{\alpha }+1)^2n+o(n)$
is asymptotically tight for
![]() $1/4\le \alpha \le 1$
. Moreover, the asymptotic behaviour of
$1/4\le \alpha \le 1$
. Moreover, the asymptotic behaviour of
![]() $r(B_{n}, B_n)$
is already known from a more general result, see [Reference Conlon5,Reference Conlon, Fox and Wigderson6]. For the remaining cases, when
$r(B_{n}, B_n)$
is already known from a more general result, see [Reference Conlon5,Reference Conlon, Fox and Wigderson6]. For the remaining cases, when
![]() $1/6\le \alpha \le 1/4$
, we only know that
$1/6\le \alpha \le 1/4$
, we only know that
![]() $r(B_{\alpha n}, B_n)\le (\frac 32+3\alpha )n+o(n)$
from Theorem 1.5. We do not know whether this upper bound is asymptotically tight or not for any
$r(B_{\alpha n}, B_n)\le (\frac 32+3\alpha )n+o(n)$
from Theorem 1.5. We do not know whether this upper bound is asymptotically tight or not for any
![]() $1/6\lt \alpha \lt 1/4$
. Note that for any
$1/6\lt \alpha \lt 1/4$
. Note that for any
![]() $1/6\lt \alpha \lt 1/4$
,
$1/6\lt \alpha \lt 1/4$
,
therefore, if
![]() $r(B_{\alpha n}, B_n)= (\frac 32+3\alpha )n+o(n)$
holds in this interval, then it means that Conjecture 1.3 proposed by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12] indeed holds in this interval. In particular, we already know that for any
$r(B_{\alpha n}, B_n)= (\frac 32+3\alpha )n+o(n)$
holds in this interval, then it means that Conjecture 1.3 proposed by Conlon, Fox, and Wigderson [Reference Conlon, Fox and Wigderson12] indeed holds in this interval. In particular, we already know that for any
![]() $\frac 16\le \alpha \lt \frac{52-16\sqrt{3}}{121}\approx 0.2007$
, Conjecture 1.3 holds from Theorem 1.6.
$\frac 16\le \alpha \lt \frac{52-16\sqrt{3}}{121}\approx 0.2007$
, Conjecture 1.3 holds from Theorem 1.6.
Acknowledgments
We are grateful to the anonymous referees for giving invaluable comments and suggestions which improve the presentation of the manuscript greatly.