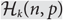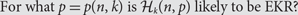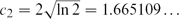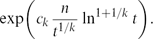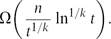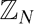6 results
On Erdős–Ko–Rado for random hypergraphs I
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 881-916
-
- Article
- Export citation
On Erdős–Ko–Rado for Random Hypergraphs II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 18 October 2018, pp. 61-80
-
- Article
- Export citation
Computing absorbing times via fluid approximations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 768-790
- Print publication:
- September 2017
-
- Article
- Export citation
The Sharp Threshold for Maximum-Size Sum-Free Subsets in Even-Order Abelian Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 609-640
-
- Article
- Export citation
Counting Independent Sets in Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 08 April 2014, pp. 539-550
-
- Article
- Export citation
Freiman Homomorphisms of Random Subsets of
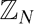 $\mathbb{Z}_{N}$
$\mathbb{Z}_{N}$
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 592-611
-
- Article
- Export citation