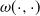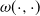2 results
Fluctuation identities for Omega-killed spectrally negative Markov additive processes and dividend problem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 404-432
- Print publication:
- June 2020
-
- Article
- Export citation
FROM RUIN TO BANKRUPTCY FOR COMPOUND POISSON SURPLUS PROCESSES
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 43 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 18 June 2013, pp. 213-243
- Print publication:
- May 2013
-
- Article
- Export citation