Article contents
Fluctuation identities for Omega-killed spectrally negative Markov additive processes and dividend problem
Published online by Cambridge University Press: 15 July 2020
Abstract
In this paper, we solve exit problems for a one-sided Markov additive process (MAP) which is exponentially killed with a bivariate killing intensity  $\omega(\cdot,\cdot)$
dependent on the present level of the process and the current state of the environment. Moreover, we analyze the respective resolvents. All identities are expressed in terms of new generalizations of classical scale matrices for MAPs. We also remark on a number of applications of the obtained identities to (controlled) insurance risk processes. In particular, we show that our results can be applied to the Omega model, where bankruptcy takes place at rate
$\omega(\cdot,\cdot)$
dependent on the present level of the process and the current state of the environment. Moreover, we analyze the respective resolvents. All identities are expressed in terms of new generalizations of classical scale matrices for MAPs. We also remark on a number of applications of the obtained identities to (controlled) insurance risk processes. In particular, we show that our results can be applied to the Omega model, where bankruptcy takes place at rate  $\omega(\cdot,\cdot)$
when the surplus process becomes negative. Finally, we consider Markov-modulated Brownian motion (MMBM) as a special case and present analytical and numerical results for a particular choice of piecewise intensity function
$\omega(\cdot,\cdot)$
when the surplus process becomes negative. Finally, we consider Markov-modulated Brownian motion (MMBM) as a special case and present analytical and numerical results for a particular choice of piecewise intensity function 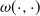 $\omega(\cdot,\cdot)$
.
$\omega(\cdot,\cdot)$
.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 3
- Cited by


