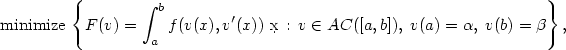We consider the following classical autonomous variational problem

\[ \textrm{minimize\,} \left\{F(v)=\int_a^b f(v(x),v'(x))\ \dx\,:\,v\in AC([a,b]), \;v(a)=\alpha,\; v(b)=\beta\right\},\]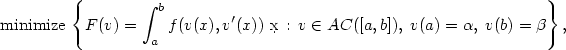

where the Lagrangian f is possibly neither continuous, nor convex, nor coercive.We prove a monotonicity property of the minimizers stating that they satisfy the maximum principle or the minimum one. By virtue of such a property, applying recent results concerning constrained variational problems, we derive a relaxation theorem, the DuBois-Reymond necessary condition and some existenceor non-existence criteria.

Local Lipschitz continuity of minimizers of certain integrals of the Calculus of Variations is obtained when the integrands are convex with respect to the gradient variable, but are not necessarily uniformly convex. In turn, these regularity results entail existence of minimizers of variational problems with non-homogeneous integrands nonconvex with respect to the gradient variable. The x-dependence, explicitly appearing in the integrands, adds significant technical difficulties in the proof.