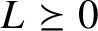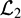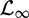3 results
Hilbert’s 17th problem in free skew fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DELAY-DEPENDENT ROBUST H∞ CONTROL FOR SINGULAR SYSTEMS WITH MULTIPLE DELAYS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 209-230
-
- Article
-
- You have access
- Export citation