Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T04:44:14.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Extended state observer-based robust non-linear integral dynamic surface control for triaxial MEMS gyroscope

Published online by Cambridge University Press:  09 November 2018

Mehran Hosseini-Pishrobat Open the ORCID record for Mehran Hosseini-Pishrobat [Opens in a new window]  and
Jafar Keighobadi
Mehran Hosseini-Pishrobat
Affiliation:
Faculty of Mechanical Engineering, University of Tabriz, 29 Bahman, Tabriz P.C. 5166614766, Iran. E-mail: [email protected]
Jafar Keighobadi*
Affiliation:
Faculty of Mechanical Engineering, University of Tabriz, 29 Bahman, Tabriz P.C. 5166614766, Iran. E-mail: [email protected]
*
*Corresponding author. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Summary

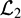This paper reports an extended state observer (ESO)-based robust dynamic surface control (DSC) method for triaxial MEMS gyroscope applications. An ESO with non-linear gain function is designed to estimate both velocity and disturbance vectors of the gyroscope dynamics via measured position signals. Using the sector-bounded property of the non-linear gain function, the design of an $\mathcal{L}_2$-robust ESO is phrased as a convex optimization problem in terms of linear matrix inequalities (LMIs). Next, by using the estimated velocity and disturbance, a certainty equivalence tracking controller is designed based on DSC. To achieve an improved robustness and to remove static steady-state tracking errors, new non-linear integral error surfaces are incorporated into the DSC. Based on the energy-to-peak (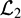$\mathcal{L}_2$-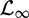$\mathcal{L}_\infty$) performance criterion, a finite number of LMIs are derived to obtain the DSC gains. In order to prevent amplification of the measurement noise in the DSC error dynamics, a multi-objective convex optimization problem, which guarantees a prescribed 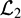$\mathcal{L}_2$-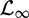$\mathcal{L}_\infty$ performance bound, is considered. Finally, the efficacy of the proposed control method is illustrated by detailed software simulations.

Keywords

Triaxial MEMS gyroscopeDynamics surface controlExtended state observerLinear matrix inequality
Type
Articles
Information
Robotica , Volume 37 , Issue 3 , March 2019 , pp. 481 - 501
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Doostdar, P. and Keighobadi, J., “Design and implementation of SMO for a nonlinear MIMO AHRS,” Mech. Syst. Signal Process. 32, 94–115 (2012).Google Scholar
2. Collin, J., Davidson, P., Kirkko-Jaakkola, M. and Leppkoski, H., “Inertial Sensors and Their Applications,” In: Handbook of Signal Processing Systems (Bhattacharyya, S. S., Deprettere, E. F., Leupers, R. and Takala, J., eds.) (Springer, New York, NY, 2013) pp. 69–96.Google Scholar
3. Zhanshe, G., Fucheng, C., Boyu, L., Le, C., Chao, L. and Ke, S., “Research development of silicon MEMS gyroscopes: A review,” Microsyst. Technol. 21 (10), 2053–2066 (2015).Google Scholar
4. Barbour, N. and Schmidt, G., “Inertial sensor technology trends,” IEEE Sensors J. 1 (4), 332–339 (2001).Google Scholar
5. John, J. D., Adaptively Controlled MEMS Triaxial Angular Rate Sensor PhD Thesis (School of Electrical and Computer Engineering, RMIT University, Melbourne, 2006).Google Scholar
6. John, J. D. and Vinay, T., “Novel concept of a single-mass adaptively controlled triaxial angular rate sensor,” IEEE Sensors J. 6, 588–595 (2006).Google Scholar
7. Acar, C. and Shkel, A., MEMS Vibratory Gyroscopes: Structural Approaches to Improve Robustness (Springer, Boston, MA, 2009).Google Scholar
8. Patel, C., McCluskey, P., “Performance Degradation of the MEMS Vibratory Gyroscope in Harsh Environments,” Proceedings of the ASME. ASME International Mechanical Engineering Congress and Exposition, Volume 11: Nano and Micro Materials, Devices and Systems; Microsystems Integration, Denver, Colorado, USA (2011) pp. 511–515.Google Scholar
9. Park, S., Adaptive Control Strategies for MEMS Gyroscopes PhD Thesis (U.C. Berkeley, Berkeley, CA, USA, 2000).Google Scholar
10. Park, S. and Horowitz, R., “New Adaptive Mode of Operation for MEMS Gyroscopes,” J. Dyn. Syst. Meas. Control 126 (4), 800–810 (2004).Google Scholar
11. Batur, C., Sreeramreddy, T. and Khasawneh, Q., “Sliding mode control of a simulated MEMS gyroscope,” ISA Trans. 45 (1), 99–108 (2006).Google Scholar
12. Zheng, Q., Dong, L., Lee, D. H. and Gao, Z., “Active disturbance rejection control for MEMS gyroscopes,” IEEE Trans. Control Syst. Technol. 17 (6), 1432–1438 (2009).Google Scholar
13. Hosseini-Pishrobat, M. and Keighobadi, J., “Force-balancing model predictive control of MEMS vibratory gyroscope sensor,” Proc. Inst. Mech. Eng., Part C: J. Mech. Eng. Sci. 230 (17), 3055–3065 (2016).Google Scholar
14. Fang, Y., Zhou, J. and Fei, J., “Robust adaptive fuzzy controller with supervisory compensator for MEMS gyroscope sensor,” Robotica 34 (10), 2330–2343 (2016).Google Scholar
15. Song, Z., Li, H. and Sun, K., “Adaptive dynamic surface control for MEMS triaxial gyroscope with nonlinear inputs,” Nonlinear Dyn. 78 (1), 173–182 (2014).Google Scholar
16. Swaroop, D., Hedrick, J. K., Yip, P. P. and Gerdes, J. C., “Dynamic surface control for a class of nonlinear systems,” IEEE Trans. Autom. Control, 45 (10), 1893–1899 (2000).Google Scholar
17. Song, B. and Hedrick, J. K., Dynamic Surface Control of Uncertain Nonlinear Systems (Springer, London, 2011).Google Scholar
18. Song, B. and Hedrick, J.K., “Design of dynamic surface control for fully-actuated mechanical systems,” IFAC Proc. Vol. 44 (1), 7363–7368 (2011).Google Scholar
19. Song, B., Hedrick, J. K. and Howell, A., “Robust stabilization and ultimate boundedness of dynamic surface control systems via convex optimization,” Int. J. Control, 75 (12), 870–881 (2002).Google Scholar
20. Zhou, L., Fei, S. and Jiang, C., “Adaptive integral dynamic surface control based on fully tuned radial basis function neural network,” J. Syst. Eng. Electron. 21 (6), 1072–1078 (2010).Google Scholar
21. Liu, X., Sun, X., Liu, S. and Xu, S., “Nonlinear gains recursive sliding mode dynamic surface control with integral action,” Asian J. Control 17 (5), 1955–1961 (2015).Google Scholar
22. Madoski, R. and Herman, P., “Survey on methods of increasing the efficiency of extended state disturbance observers,” ISA Trans. 56, 18–27 (2015).Google Scholar
23. Younis, M.I., MEMS Linear and Nonlinear Statics and Dynamics (Springer, Boston, MA, 2011).Google Scholar
24. Boyd, S., Ghaoui, L. E., Feron, E. and Balakrishnan, V., Linear Matrix Inequalities in System Control Theory, Society for Industrial and Applied Mathematics, (1994).Google Scholar
25. Xian, B., Dawson, D. M., deQueiroz, M. S. and Chen, J. “A continuous asymptotic tracking control strategy for uncertain nonlinear systems,” IEEE Trans. Autom. Control 49 (7), 1206–1206 (2004).Google Scholar
26. Zhao, B., Xian, B., Zhang, Y. and Zhang, X., “Nonlinear robust adaptive tracking control of a quadrotor UAV via immersion and invariance methodology,” IEEE Trans. Ind. Electron. 62 (5), 2891–2902 (2015).Google Scholar
27. Skelton, R.E., Iwasaki, T. and Grigoriadis, K. M., A Unified Algebraic Approach to Linear Control Design (Taylor & Francis, London, 1997).Google Scholar
28. Polycarpou, M. M. and Ioannou, P. A., “A robust adaptive nonlinear control design,” Automatica 32 (3), 423–427 (1996).Google Scholar
29. Grant, M. 1. and Boyd, S., “Graph Implementations for Nonsmooth Convex Programs,” In: Recent Advances in Learning and Control (Blondel, V. D., Boyd, S. P. and Kimura, H., eds.) (Springer-Verlag Limited, 2008) pp. 95–110.Google Scholar
30. Grant, M., Boyd, S., “CVX: Matlab Software for Disciplined Convex Programming,” version 2.1, cvxr.com/cvx, (2014).Google Scholar
31. Kempe, V., “Gyroscopes,” In: Inertial MEMS: Principles and Practice (Cambridge University Press, Cambridge, 2011), pp. 364–459.Google Scholar