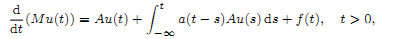Let A and M be closed linear operators defined on a complex Banach space X and let a ∈ L1(ℝ+) be a scalar kernel. We use operator-valued Fourier multipliers techniques to obtain necessary and sufficient conditions to guarantee the existence and uniqueness of periodic solutions to the equation
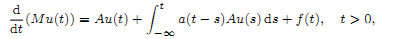
with initial condition Mu(0) = Mu(2π), solely in terms of spectral properties of the data. Our results are obtained in the scales of periodic Besov, Triebel–Lizorkin and Lebesgue vector-valued function spaces.