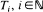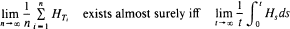It is known (Weizsäcker and Winkler (1990)) that for bounded predictable functions H and a Poisson process with jump times 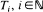
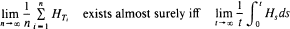 exists almost surely, and that in this case both limits are equal. Here we relax the boundedness condition on H. Our tool is a law of large numbers for local L2-martingales. We show by examples that our condition is close to optimal. Furthermore we indicate a generalization to point processes on more general spaces. The above property is called PASTA (‘Poisson arrivals see time averages') and is heavily used in queueing theory.
exists almost surely, and that in this case both limits are equal. Here we relax the boundedness condition on H. Our tool is a law of large numbers for local L2-martingales. We show by examples that our condition is close to optimal. Furthermore we indicate a generalization to point processes on more general spaces. The above property is called PASTA (‘Poisson arrivals see time averages') and is heavily used in queueing theory.