1 results
On a stochastic difference equation and a representation of non–negative infinitely divisible random variables
-
- Journal:
- Advances in Applied Probability / Volume 11 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 01 July 2016, pp. 750-783
- Print publication:
- December 1979
-
- Article
- Export citation
-
The present paper considers the stochastic difference equation Yn = AnYn-1 + Bn with i.i.d. random pairs (An, Bn) and obtains conditions under which Yn converges in distribution. This convergence is related to the existence of solutions of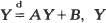
and (A, B) independent, and the convergence w.p. 1 of ∑ A1A2 ··· An-1Bn. A second subject is the series ∑ Cnf(Tn) with (Cn) a sequence of i.i.d. random variables, (Tn) the sequence of points of a Poisson process and f a Borel function on (0, ∞). The resulting random variable turns out to be infinitely divisible, and its Lévy–Hinčin representation is obtained. The two subjects coincide in case An and Cn are independent, Bn = AnCn, An = U1/αn with Un a uniform random variable, f(x) = e−x/α.
and (