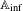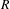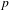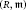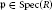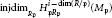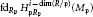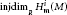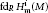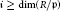6 results
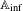 $\mathbb{A}_{\text{inf}}$ IS INFINITE DIMENSIONAL
$\mathbb{A}_{\text{inf}}$ IS INFINITE DIMENSIONAL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 11 May 2020, pp. 1983-1989
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
Classification of Simple Weight Modules over the Schrödinger Algebra
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 16-39
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
KRULL DIMENSION IN MODAL LOGIC
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1356-1386
- Print publication:
- December 2017
-
- Article
- Export citation
A Note on Homological Dimensions of Artinian Local Cohomology Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 491-499
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
BOUNDED AND FULLY BOUNDED MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 04 October 2011, pp. 433-440
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Unruly Hilbert Domains
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 1 / 01 March 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 106-109
- Print publication:
- 01 March 1990
-
- Article
-
- You have access
- Export citation