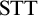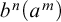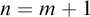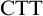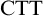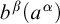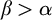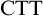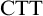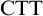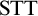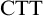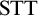1 results
AGAINST CUMULATIVE TYPE THEORY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2021, pp. 907-949
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Standard Type Theory,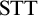
${\textrm {STT}}$, tells us that 
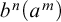$b^n(a^m)$ is well-formed iff 
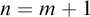$n=m+1$. However, Linnebo and Rayo [23] have advocated the use of Cumulative Type Theory, 
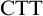$\textrm {CTT}$, which has more relaxed type-restrictions: according to 
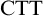$\textrm {CTT}$, 
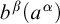$b^\beta (a^\alpha )$ is well-formed iff 
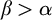$\beta>\alpha $. In this paper, we set ourselves against 
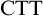$\textrm {CTT}$. We begin our case by arguing against Linnebo and Rayo’s claim that 
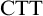$\textrm {CTT}$ sheds new philosophical light on set theory. We then argue that, while 
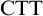$\textrm {CTT}$’s type-restrictions are unjustifiable, the type-restrictions imposed by 
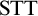${\textrm {STT}}$ are justified by a Fregean semantics. What is more, this Fregean semantics provides us with a principled way to resist Linnebo and Rayo’s Semantic Argument for 
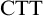$\textrm {CTT}$. We end by examining an alternative approach to cumulative types due to Florio and Jones [10]; we argue that their theory is best seen as a misleadingly formulated version of 
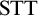${\textrm {STT}}$.
