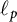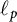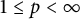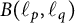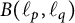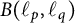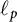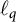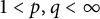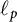1 results
Differentiability of the operator norm on
$\ell _p$ spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper, we present a characterization of strong subdifferentiability of the norm of bounded linear operators on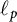
$\ell _p$ spaces, 
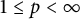$1\leq p<\infty $. Furthermore, we prove that the set of all bounded linear operators in 
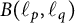${B}(\ell _p, \ell _q)$ for which the norm of 
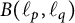${B}(\ell _p, \ell _q)$ is strongly subdifferentiable is dense in 
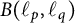${B}(\ell _p, \ell _q)$. Additionally, we present a characterization of Fréchet differentiability of the norm of bounded linear operators from 
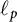$\ell _p$ to 
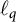$\ell _q$, where 
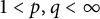$1 < p, q < \infty $. Applying this result, we will show that the Fréchet differentiability and the Gateaux differentiability of the norm of bounded linear operators on 
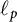$\ell _p$ spaces coincide, extending a known theorem regarding the operator norm on Hilbert 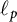spaces.
