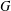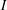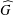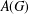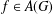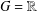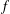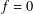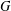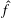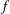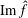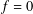1 results
A COMPACT QUALITATIVE UNCERTAINTY PRINCIPLE FOR SOME NONUNIMODULAR GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 114-120
- Print publication:
- February 2019
-
- Article
-
- You have access
- Open access
- Export citation
-
Let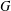
$G$ be a separable locally compact group with type 
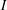$I$ left regular representation, 
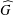$\widehat{G}$ its dual, 
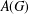$A(G)$ its Fourier algebra and 
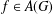$f\in A(G)$ with compact support. If 
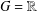$G=\mathbb{R}$ and the Fourier transform of 
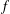$f$ is compactly supported, then, by a classical Paley–Wiener theorem, 
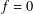$f=0$. There are extensions of this theorem for abelian and some unimodular groups. In this paper, we prove that if 
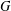$G$ has no (nonempty) open compact subsets, 
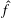$\hat{f}$, the regularised Fourier cotransform of 
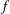$f$, is compactly supported and 
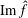$\text{Im}\,\hat{f}$ is finite dimensional, then 
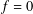$f=0$. In connection with this result, we characterise locally compact abelian groups whose identity components are noncompact.
