Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T03:20:53.355Z Has data issue: false hasContentIssue false
  • English
  • Français

A COMPACT QUALITATIVE UNCERTAINTY PRINCIPLE FOR SOME NONUNIMODULAR GROUPS

Part of: Abstract harmonic analysis

Published online by Cambridge University Press:  28 November 2018

WASSIM NASSERDDINE Open the ORCID record for WASSIM NASSERDDINE [Opens in a new window]
WASSIM NASSERDDINE*
Affiliation:
Faculty of Sciences – Section I, Lebanese University, 2905-3901 Hadath, Beirut, Lebanon email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 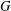$G$ be a separable locally compact group with type 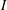$I$ left regular representation, 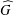$\widehat{G}$ its dual, 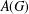$A(G)$ its Fourier algebra and 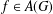$f\in A(G)$ with compact support. If 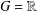$G=\mathbb{R}$ and the Fourier transform of 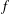$f$ is compactly supported, then, by a classical Paley–Wiener theorem, 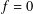$f=0$. There are extensions of this theorem for abelian and some unimodular groups. In this paper, we prove that if 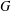$G$ has no (nonempty) open compact subsets, 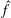$\hat{f}$, the regularised Fourier cotransform of 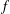$f$, is compactly supported and 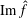$\text{Im}\,\hat{f}$ is finite dimensional, then 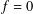$f=0$. In connection with this result, we characterise locally compact abelian groups whose identity components are noncompact.

Keywords

Paley–Wiener propertyqualitative uncertainty principleFourier algebraFourier transformationFourier cotransformation

MSC classification

Primary: 43A30: Fourier and Fourier-Stieltjes transforms on nonabelian groups and on semigroups, etc.
Secondary: 43A25: Fourier and Fourier-Stieltjes transforms on locally compact and other abelian groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 114 - 120
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© 2018 Australian Mathematical Publishing Association Inc.

Footnotes

This project has been funded with support from the Lebanese University.

References

Arnal, D. and Ludwig, J., ‘Q.U.P. and Paley–Wiener properties of unimodular, especially Lie groups’, Proc. Amer. Math. Soc. 125(4) (1997), 1071–1080.Google Scholar
Duflo, M. and Moore, C. C., ‘On the regular representation of a nonunimodular locally compact group’, J. Funct. Anal. 21(2) (1976), 209–243.Google Scholar
Eymard, P. and Terp, M., ‘La transformation de Fourier et son inverse sur le groupe des ax + b d’un corps local’, in: Analyse harmonique sur les groupes de Lie (Sém. Nancy–Strasbourg 1976–1978), II, Lecture Notes in Mathematics, 739 (Springer, Berlin, 1979), 207–248.Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, Vol. I, 2nd edn, Grundlehren der mathematischen Wissenschaften, 115 (Springer, New York, 1979).Google Scholar
Hogan, J. A., ‘A qualitative uncertainty principle for locally compact abelian groups’, in: Miniconf. Harmonic Analysis and Operator Algebras, Canberra, 1987, Proceedings of the Centre for Mathematical Analysis, Australian National University, Canberra, 16 (1988), 133–142.Google Scholar
Hogan, J. A., ‘A qualitative uncertainty principle for unimodular groups of type I’, Trans. Amer. Math. Soc. 340 (1993), 587–594.Google Scholar
Kaniuth, E., ‘Minimizing functions for an uncertainty principle on locally compact groups of bounded representation dimension’, Proc. Amer. Math. Soc. 135 (2007), 217–227.Google Scholar
Kaniuth, E., ‘Qualitative uncertainty principles for groups with finite dimensional irreducible representations’, J. Funct. Anal. 257 (2009), 340–356.Google Scholar
Kaniuth, E., Lau, A. T. and Schlichting, G., ‘A topological Paley–Wiener property for locally compact groups’, Proc. Amer. Math. Soc. 133(7) (2005), 2157–2164.Google Scholar
Kutyniok, G., ‘A weak qualitative uncertainty principle for compact groups’, Illinois J. Math. 47 (2003), 709–724.Google Scholar
Lipsman, R. L., ‘Non-abelian Fourier analysis’, Bull. Sci. Math. (2) 98 (1974), 209–233.Google Scholar
Nasserddine, W., ‘Sur le groupe affine d’un corps local’, C. R. Math. Acad. Sci. Paris Ser. I 342(7) (2006), 493–495.Google Scholar
Nasserddine, W., ‘Une caractérisation de l’algèbre de Fourier pour certains groupes localement compacts’, C. R. Math. Acad. Sci. Paris Ser. I 355 (2017), 543–548.Google Scholar
Nasserddine, W., ‘Some Fourier analysis results on certain non-abelian groups’, submitted.Google Scholar