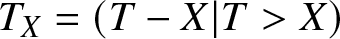1 results
The mean residual life at random age and its connection to variability measures
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 19 February 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We consider a nonnegative random variable T representing the lifetime of a system. We discuss the residual lifetime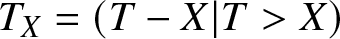
$T_X=(T-X|T \gt X)$, where X denotes the random age of the system. We also discuss the mean residual life (MRL) of T at the random time X. It is shown that the MRL at random age (MRLR) is closely related to some well-known variability measures. In particular, we show that the MRLR can be considered a generalization of Gini’s mean difference (GMD). Under the proportional hazards model, we show that the MRLR gives the extended GMD and the extended cumulative residual entropy as special cases. Then, we provide a decomposition result indicating that the MRLR has a covariance representation. Some comparison results are also established for the MRLs of two systems at random ages.
