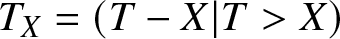The mean residual life at random age and its connection to variability measures

Abstract

We consider a nonnegative random variable T representing the lifetime of a system. We discuss the residual lifetime $T_X=(T-X|T \gt X)$, where X denotes the random age of the system. We also discuss the mean residual life (MRL) of T at the random time X. It is shown that the MRL at random age (MRLR) is closely related to some well-known variability measures. In particular, we show that the MRLR can be considered a generalization of Gini’s mean difference (GMD). Under the proportional hazards model, we show that the MRLR gives the extended GMD and the extended cumulative residual entropy as special cases. Then, we provide a decomposition result indicating that the MRLR has a covariance representation. Some comparison results are also established for the MRLs of two systems at random ages.

1. Introduction

1.1. Background and related literature

The mean residual life (MRL) is a valuable concept in a wide range of fields, such as reliability engineering and survival analysis, providing insights into the expected remaining life of entities or systems. In reliability engineering, the MRL is used to assess the remaining lifetime of systems and components that have survived up to a certain point of time t. Engineers can use it to make predictions about the remaining useful life of machinery or equipment. In the medical field, survival analysis involves studying the time until an event of interest occurs, such as death. The MRL is used to estimate the average remaining lifespan for patients who have already survived for a certain duration. In the last few decades, a large number of research works have been reported in the literature on various aspects of the theory and applications of MRL. We refer the reader to [16] for the theory and applications of the MRL.

Let T be a continuous nonnegative random variable describing the life of a live organism. If T has the survival function $\bar{F}(t)=P(T \gt t)$ and a finite mean µ, then the MRL of T at age t is defined as

\begin{equation*} m(t)\equiv E(T-t|T \gt t)=\frac{\int_{t}^{\infty}\bar{F}(x)dx}{\bar{F}(t)}, \end{equation*}

for t such that $\bar{F}(t) \gt 0$. Note that $m(0)=\mu$ and by the finiteness of µ, we have $m(t) \lt \infty$, for all $t\in(0,\infty)$. As we mentioned, the MRL is a widely used tool in the study and modeling the lifetime data in reliability engineering and survival analysis. We refer the reader, among others, to [22] for the concept and some related theoretical results on MRL. [17] studied discrete bathtub and upside-down bathtub MRLs. [30] showed that the survival function $\bar{F}$ satisfies a variant of lack of memory property involving the MRL, if and only if the MRL is a linear function of time. They also defined the concept of proportional MRLs. [1] used the local linear fitting technique to estimate the MRL. Asadi and Bayramoglu [4] studied the MRL of coherent systems under different conditions. [34] studied a model for an upside-down bathtub-shaped MRL and explored its properties. [35] gave a nonparametric estimator to estimate decreasing MRL based on type II censored data. [12] studied the proportional MRLs model to analyze the survival data in the presence of censored observations. [9] explored the MRL of a system with two dependent components per element. [20] used the MRL as a condition index in condition-based maintenance for decision-making. [25] studied the role of dependence in residual lifetimes in a two-component system. [41] estimated the MRL based on ranked set sampling. [42] studied stochastic comparisons of conditional residual lifetimes and gave some applications.

The MRL has applications in other branches, including extreme value theory, hydrology, actuarial science, environmental science, etc. (see, for example, [15] and references therein).

The residual lifetime at the random age has also been considered in the literature. Let T be a random variable representing the lifetime of a system/device. Let X denote the random age of the system. Then the residual lifetime of the system, given that it survives at random time X, is

\begin{equation*} T_X=(T-X|T \gt X).\end{equation*}

The residual life at random time has applications in different areas, such as queueing theory [26, 37] and reliability [27]. We also refer the reader to [13, 24], and [10] and references therein on some stochastic ordering and preservation results on the residual life at random times under certain classes of aging.

Another notion of random age has also been considered in the literature. Consider a homogeneous population of statistically identical items with lifetime T. Assume that each item has been operating for some time that varies from item to item. Therefore, an item selected randomly from the population can be described by its random age X whose remaining lifetime is a random variable T_X depending on the random age X (see Remark 3.7). We refer to [11, 14, 19] and [6] for details on this notion of random age.

1.2. Contributions of the paper

We consider a non-negative random variable T, which represents the lifetime of a system. Within this context, we investigate the concept of residual lifetime, $T_X=(T-X|T \gt X)$, where X represents the random age of the system. Our discussion centrs on the mean of T_X, which we call the MRL at random age (MRLR) and denote by ${\mathbb{E}}(T_X)$. The analysis reveals a close connection between ${\mathbb{E}}(T_X)$ and several well-known measures of variability. Notably, our proposed MRLR can be viewed as an extension of Gini’s mean difference (GMD). Under the proportional hazards model, we illustrate how the MRLR ${\mathbb{E}}(T_X)$ yields both the extended GMD and the extended cumulative residual entropy (CRE) as special cases. Furthermore, we present a decomposition result, exploring that the MRLR ${\mathbb{E}}(T_X)$ can be represented in terms of covariance functionals and the expected values of T and X, respectively. Finally, we present a copula-based representation of the MRLR ${\mathbb{E}}(T_X)$ in the case that T and X are dependent.

1.3. Organization of the paper

The organization of the paper is as follows: In Section 2, we first give some preliminary results that are useful in subsequent sections. In Section 3, after representing various forms of the MRLR ${\mathbb{E}}(T_X)$, we show that, by choosing different forms for the distribution of X, ${\mathbb{E}}(T_X)$ is connected to different measures of variability. We show that the MRLR ${\mathbb{E}}(T_X)$ can be represented as the conditional expectation of the ordinary MRL of T and the conditional expectation of the mean inactivity time (MIT) of X. Section 4 is devoted to a covariance representation of ${\mathbb{E}}(T_X)$ resulting in some useful inequalities for the MRLR. In Section 5, we give a copula-based representation of the MRLR ${\mathbb{E}}(T_X)$ for the case that T and X are dependent. The paper is finalized with some concluding remarks in Section 6

2. Some variability measures

Various measures have been introduced in the literature to quantify the variability of the probability distribution of a random variable. In this section, we revisit some of the most applied ones in the context of our discussion. Let us consider a continuous random variable T with a distribution function $F(t)=P(T\leq t)$, where $t\in \mathcal{A}\subseteq R$. The most popular measure of variability associated with T is the variance defined as $\mathrm{Var}(T)={\mathbb{E}}(T-\mu)^2$, where $\mu={\mathbb{E}}(T)$. The most similar index of variability to the variance with applications in finance and other fields is GMD. The GMD shares many properties with the variance but can be more informative about the properties of distributions that depart from normality (see Yithzaki [38]). The GMD corresponding to T is defined as

(1)\begin{equation} \mathrm{GMD}(T)= {\mathbb{E}}(|T_1-T_2|)=2\int F(x)\bar{F}(x)dx, \end{equation}

where T ₁ and T ₂ are independent random variables distributed as T. One can easily verify that GMD $(T)=4\mathrm{Cov}(T, F(T))$ (see [40]). [5] have shown that GMD can be represented as $\mathrm{GMD}(T)=2{\mathbb{E}}\big(m_{2}({T})\big)$, where

\begin{equation*} m_{2}(t)=\frac{\int_{t}^{\infty}\bar{F}^{2}(x)dx}{\bar{F}^{2}(t)}.\end{equation*}

Note that $m_{2}(t)$ can be considered as the MRL of a two-component series system with independent components.

The extended GMD, denoted by $\mathrm{EGi}_\nu(T)$, is proposed as a parametric extension of the GMD(T) in the following way:

\begin{equation*} \mathrm{EGi}_\nu(T)=\int_{0}^{\infty}\left(\bar{F}(t)-\bar{F}^{\nu}(t)\right)dt\quad v \gt 0. \end{equation*}

One can verify that $\mathrm{EGi}_\nu(T)$ has the following covariance representation (see [39]).

\begin{equation*}\mathrm{EGi}_\nu(T)=\nu \left[I(0 \lt \nu \lt 1)-I(\nu \gt 1)\right]\mathrm{Cov}(T,\bar{F}^{\nu-1}(T)),\end{equation*}

where I(A) is the indicator function defined over the set A, and ν is a parameter that ranges from 0 to infinity and determines the relative weight attributed to “various portions” of the probability distribution. Obviously, for ν = 2, the extended Gini difference reduces to GMD(T) (up to a constant). Another representation of $\mathrm{EGi}_\nu(T)$ is as $\mathrm{EGi}_\nu(T)= (\nu-1){\mathbb{E}}(m_{\nu}(T))$ (see [5]), where

\begin{equation*} m_{\nu}(t)=\frac{\int_{t}^{\infty}\bar{F}^{\nu}(x)dx}{\bar{F}^{\nu}(t)}. \end{equation*}

For more interpretations and applications of $\mathrm{EGi}_\nu(T)$ in economic studies based on different values of ν, we refer to [40].

Another popular in the literature of information theory measures is the CRE, defined by [31] as

(2)\begin{equation} \mathcal{E}(T)\equiv-\int_{0}^{\infty}\bar{F}(x)\log\bar{F}(x)dx. \end{equation}

As an alternative to the Shannon entropy measure, the cited authors argued that the CRE can be considered as a measure of uncertainty. They obtained several properties of the CRE and provided applications in computer vision. Matching two or more images under diverse conditions like pose, acquisition parameters, etc., is prevalent in fields such as computer vision, medical imaging, geographical information systems, and more. In recent years, information-theoretic measures have become extensively utilized in defining cost functions to optimize these matches. Motivated by this, [31] have utilized the concept of CRE as a valuable tool for image alignment in computer vision. It was reported by [3] that the following equality holds for a non-negative random variable

(3)\begin{equation} \mathcal{E}(T)=\mathrm{Cov}(T,\Lambda(T)), \end{equation}

where $\Lambda(x)=-\log\bar{F}(x)$, is the cumulative failure rate. It was also noticed by [8] that the CRE is closely related to the mean remaining lifetime, m(t), of a non-negative random variable T. In fact, it is always true that the CRE can be represented as $\mathrm{CRE}={\mathbb{E}}(m(T))$.

3. MRL at random age

Let T be a random variable representing the lifetime of a system/device. Let X (independent of T) denote the random age of the system. Then, the residual lifetime of the system, given that it survives at time X, is

(4)\begin{equation} T_X=(T-X|T \gt X). \end{equation}

Assume that F(G) denotes the distribution function of T(X) and denote the corresponding reliability function by $\bar{F}=1-F$( $\bar{G}=1-G)$. Then, the reliability function of T_X is given as

(5)\begin{align} P(T_{X} \gt t)&=P(T-X \gt t|T \gt X)\nonumber\\[4pt] &=\frac{P(T \gt t+X)}{P(T \gt X)}\nonumber\\[4pt] &=\frac{\int_{0}^{\infty}{P(T \gt t+x|X=x)}dG(x)}{\int_{0}^{\infty}{P(T \gt x|X=x)}dG(x)}\nonumber\\[4pt] &=\frac{\int_{0}^{\infty}{\bar{F}(t+x)}dG(x)}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}, \end{align}

where the third equality follows from the assumption of independence between T and X.

A measure of interest in many applications may be the MRLR of T_X, denoted by ${\mathbb{E}}(T_X)$, given by

\begin{equation*} {\mathbb{E}}(T_X)=\int_{0}^{\infty}P(T_{X} \gt t)dt= \frac{\int_{0}^{\infty}\left(\int_{0}^{\infty}{\bar{F}(t+x)}dG(x)\right)dt}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}. \end{equation*}

The next proposition gives a representation of ${\mathbb{E}}(T_X)$.

Proposition 3.1. The MRLR ${\mathbb{E}}(T_X)$ can be represented as

(6)\begin{equation} {\mathbb{E}}(T_X)= \frac{\int_{0}^{\infty}{\bar{F}(t)}G(t)dt }{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}. \end{equation}

Proof. We have

\begin{align*} {\mathbb{E}}(T_X)&= \frac{\int_{0}^{\infty}\left(\int_{0}^{\infty}{\bar{F}(t+x)}dG(x)\right)dt}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\[4pt] &=\frac{\int_{0}^{\infty}\left(\int_{x}^{\infty}{\bar{F}(t)}dt\right)dG(x)}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\[4pt] &=\frac{\int_{0}^{\infty}{\bar{F}(t)}\left(\int_{0}^{t}{dG(x)}\right)dt}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\[4pt] &=\frac{\int_{0}^{\infty}{\bar{F}(t)}G(t)dt }{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}.\end{align*}

Remark 3.2. We must emphasize that while, in general, T and X may be dependent, there are instances in real-life scenarios where they can be independent. For instance, consider a system with a lifetime T that commences operation at t = 0. The system is then monitored by an operator at a random time X, where X (the time of inspection) can be entirely independent of T (the system’s lifetime). In cases where T and X are dependent, and their joint distribution can be modeled by a copula, we provide a brief discussion on the general form of ${\mathbb{E}}(T_X)$ in Section 5.

An interpretation of MRLR

It is known that the GMD can be interpreted as follows: Let one be interested in measuring the variability of a certain quantity in a population of individuals. He or she may draw a random sample of two observations and record the absolute difference between them. Then, the GMD can be interpreted as the expected absolute difference between two randomly drawn members from the population. As an extension of GMD, $E(T_X)$ can be interpreted as a general measure of variability as follows. Consider an investigator who is interested in measuring the variability of a certain quantity (T) in the population with respect to a reference population (X) (given that T > X). The investigator draws a random observation from T and one observation from X and records the difference between them. Repeating the sampling procedure an infinite number of times and averaging the differences yield the $E(T_X)$. Hence, the $E(T_X)$ can be interpreted as the expected difference between two randomly drawn members from the two populations. In Section 3.1, we show that by selecting specific forms for the distribution functions of X, the MRLR ${\mathbb{E}}(T_X)$ becomes associated with well-known variability measures.

Corollary 3.3. Note that, based on the representation (6), the MRLR ${\mathbb{E}}(T_X)$ can also be written as follows:

\begin{align*} {\mathbb{E}}(T_X) &=\frac{\int_{0}^{\infty}{\bar{F}(t)}-\int_{0}^{\infty}\bar{F}(t)\bar{G}(t)dt }{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\ &=\frac{{\mathbb{E}}(T)-{\mathbb{E}}(\min(T,X)) }{{\mathbb{E}}(\bar{F}(X))}\\ &=\frac{{\mathbb{E}}(T)-{\mathbb{E}}(\min(T,X)) }{{\mathbb{E}}({G}(T))}. \end{align*}

It can similarly seen that the MRLR ${\mathbb{E}}(T_X)$ can also be represented as follows:

\begin{align*} {\mathbb{E}}(T_X) &=\frac{{\mathbb{E}}(\max(T,X)) -{\mathbb{E}}(X)}{{\mathbb{E}}({G}(T))}\\ &=\frac{{\mathbb{E}}(\max(T,X)) -{\mathbb{E}}(X)}{{\mathbb{E}}(\bar{F}(X))}. \end{align*}

As illustrations of the MRLR, let us look at the following examples.

Example 3.4. Let T be distributed as exponential distribution with reliability function $\bar{F}(t)=e^{-\lambda t},$ t > 0, λ > 0, and X be distributed as an arbitrary distribution $\bar{G}(t)$ on real positive line. Then, it can be easily seen (based on the memoryless property of the exponential distribution) that

\begin{align*} P(T_{X} \gt t) &=\frac{\int_{0}^{\infty}e^{-\lambda(t+x)}dG(x)dt}{\int_{0}^{\infty}{e^{-\lambda x}}dG(x)}\\ &=e^{-\lambda t}. \end{align*}

That is, T_X has an exponential distribution with parameter λ and thus ${\mathbb{E}}(T_X)=\lambda^{-1}$.

Example 3.5. Let T and X be distributed as Pareto distributions, respectively, with reliability functions $\bar{F}(t)=\big(\frac{1}{1+t}\big)^\alpha,$ t > 0, α > 0, and $\bar{G}(t)=\big(\frac{1}{1+t}\big)^\beta$, t > 0, β > 0. Then, we have

\begin{align*} {\mathbb{E}}_{\alpha,\beta}(T_X)&= \frac{\int_{0}^{\infty}{\bar{F}(t)}G(t)dt }{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\ &= \frac{\int_{0}^{\infty}{\big(\frac{1}{1+t}\big)^\alpha}\left(1-\big(\frac{1}{1+t}\big)^\beta\right)dt }{\int_{0}^{\infty}{\beta \big(\frac{1}{1+t}\big)^{\alpha+\beta+1}}dt}\\ &= \frac{\alpha+\beta}{(\alpha-1)(\alpha+\beta-1)},\quad \alpha \gt 1. \end{align*}

It can be seen that for fixed value β, the MRLR ${\mathbb{E}}_{\alpha,\beta}(T_X)$ is a decreasing function of α. If we assume here that the Pareto distribution with fixed parameter β ₀ is a reference distribution, then ${\mathbb{E}}_{\alpha,\beta_0}(T_X)$ as function α can be interpreted as a measure of variability, which shows the variability of Pareto distribution with shape parameter α with respect to the reference Pareto distribution with shape parameter β ₀. Here, we observe that for $\alpha_1 \lt \alpha_2$, then ${\mathbb{E}}_{\alpha_1,\beta_0}(T_X)\leq {\mathbb{E}}_{\alpha_2,\beta_0}(T_X)$ showing that the Pareto distribution with shape parameter α ₁ is less variable than the Pareto distribution with shape parameter α ₂ in terms of reference Pareto distribution with shape parameter β ₀.

Figure 1. The plot of MRLR ${\mathbb{E}}_\alpha(T_X)$ as a function α for Weibull (left) and Pareto (right) distributions with shape parameter α with random age distributed as exponential.

Example 3.6. We consider two cases:

• • Let T be distributed as Weibull distribution, with reliability function $\bar{F}(t)=e^{-t^{\alpha}},$ t > 0, α > 0, and X be distributed as exponential with reliability function $\bar{G}(t)=e^{-t}$, t > 0. Then, we have

  \begin{align*} {\mathbb{E}}_{\alpha}(T_X)&= \frac{\int_{0}^{\infty}{\bar{F}(t)}G(t)dt }{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\ &=\frac{\int_{0}^{\infty}e^{-t^\alpha}dt}{\int_{0}^{\infty}e^{-t^\alpha-t}dt }-1. \end{align*}

  The MRLR ${\mathbb{E}}_{\alpha}(T_X)$ here does not have a closed form. A plot of ${\mathbb{E}}_{\alpha}(T_X)$, as a function of α, is given in Figure 1 (left). It is seen that ${\mathbb{E}}_{\alpha}(T_X)$ is a decreasing function of α.

• • Let T be distributed as Pareto distribution, with reliability function $\bar{F}(t)=\left(\frac{1}{1+t}\right)^\alpha,$ t > 0, α > 0, and X be distributed as exponential with reliability function $\bar{G}(t)=e^{-t}$, t > 0. Then, we have

  \begin{equation*} {\mathbb{E}}_{\alpha}(T_X)=\frac{\int_{0}^{\infty}\left({1+t}\right)^{-\alpha} dt}{\int_{0}^{\infty}\left({1+t}\right)^{-\alpha} e^{-t}dt}-1. \end{equation*}

  The MRLR ${\mathbb{E}}_{\alpha}(T_X)$ here also does not have a closed form. A plot of ${\mathbb{E}}_{\alpha}(T_X)$ is given in Figure 1 (right) as a function of α. It is seen that the MRLR ${\mathbb{E}}_{\alpha}(T_X)$ is a decreasing function of α.

Remark 3.7. As we mentioned in the Introduction section, another notion of residual life at random age is defined in the literature. Consider a homogeneous population of statistically identical items with random generic lifetimes denoted by T. Assume that each item has been operating for some time that varies from item to item. Therefore, an item selected randomly from the population can be described by its random age X. As a practical example, we can think about manufactured components of used items with a random age X. Let $T^*_{X}$ be the remaining lifetime of the selected item at the random age X. If the cdf of X is denoted by G, then under the independence condition, $T^*_X$ has the survival function

\begin{equation*} P(T^*_X \gt t)= \int_{0}^{\infty}\left(\frac{\bar{F}(t+x)}{\bar{F}(x)}\right)dG(x). \end{equation*}

Recently, [6] investigated several properties of $E(T^*_{X})$ and its connections to variability measures. Note that the reliability functions of T_X (defined in (4)) and $T^*_X$ are connected as

\begin{align*} P(T_X \gt t)&= \frac{\int_{0}^{\infty}{\bar{F}(t+x)}dG(x)}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\ &=\frac{\int_{0}^{\infty}{\frac{\bar{F}(t+x)}{\bar{F}(x)}}\bar{F}(x)dG(x)}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\ &=\int_{0}^{\infty}\frac{\bar{F}(t+x)}{\bar{F}(x)}g^*(x)dx =P(T^{*}_{X} \gt t), \end{align*}

where $g^{*}(x)$ is the conditional distribution of $(X|T \gt X)$ given as

\begin{equation*}g^{*}(t)=\frac{\bar{F}(t)dG(t)}{\int_{0}^{\infty}\bar{F}(t)dG(t)}, \quad t \gt 0.\end{equation*}

We refer also to [23] for more results on these notions of residual life at random ages.

3.1. Some important special cases

In the following, we demonstrate that by selecting specific forms for the distribution function of X, the MRLR ${\mathbb{E}}(T_X)$, becomes associated with well-known variability measures.

• • Extended GMD: Assume that T and X have proportional hazards, i.e., there exists α > 0, such that the reliability function of X is given as $\bar{G}(x)=\bar{F}^{\alpha}(x)$. Then the corresponding MRLR, denoted by ${\mathbb{E}}_{\alpha}(T_X)$ is obtained as

  (7)\begin{align} {\mathbb{E}}_{\alpha}(T_X) &=\frac{\int_{0}^{\infty}{\bar{F}(t)}G(t)dt }{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\nonumber\\ &=\frac{\int_{0}^{\infty}{\bar{F}(t)}\left(1-\bar{F}^{\alpha}(t)\right)dt }{\alpha\int_{0}^{\infty}{\bar{F}(x)}\bar{F}^{\alpha-1}(t)dF(t)}\nonumber\\ &=\frac{\alpha+1}{\alpha}\left({\int_{0}^{\infty}\left(\bar{F}(t)-\bar{F}^{\alpha+1}(t)\right)dt }\right)\nonumber\\ &=\frac{\alpha+1}{\alpha}\mathrm{EGi}_{\alpha+1}(T), \end{align}

  where $\mathrm{EGi}_{\alpha+1}(T)$ is the extended GMD of order α + 1. In particular when α = 1, i.e., T and X have the same distribution, then we arrive at the GMD(T). That is,

  \begin{equation*} {\mathbb{E}}_{1}(T_X)= 2{\int_{0}^{\infty}\left(\bar{F}(t)-\bar{F}^{2}(t)\right)dt }={\rm GMD}(T), \end{equation*}

  Note, using the fact that the extended GMD has the following covariance representation,

  \begin{equation*} \mathrm{EGi}_{\alpha}(T)=-\alpha {\rm Cov}\big(T, \bar{F}^{\alpha-1}(T)\big), \end{equation*}

  we have

  (8)\begin{equation} {\mathbb{E}}_\alpha(T_X)= -\frac{(\alpha+1)^2}{\alpha} {\rm Cov}\big(T, \bar{F}^{\alpha}(T)\big). \end{equation}

  In particular that α = 1, we arrive at

  \begin{equation*} {\mathbb{E}}_1(T_X)= 4 {\rm Cov}\big(T, {F}(T)\big). \end{equation*}

• • Cumulative residual entropy: Using the fact that for any x > 0,

  \begin{equation*}\lim_{\alpha\rightarrow 0}\frac{1-x^\alpha}{\alpha}=-\log x,\end{equation*}

  we obtain from (7) the CRE $\mathcal{E}(X)$ in (2). That is,

  \begin{equation*}\begin{array}{ll} \lim\limits_{\alpha\rightarrow 0}{\mathbb{E}}_{\alpha}(T_{X})&=\lim\limits_{\alpha\rightarrow 0}\frac{\alpha+1}{\alpha}\mathrm{EGi}_{\alpha+1}(T)\\ &=-\int_{0}^{\infty}\bar{F}(x)\log\bar{F}(x)dx \\ &=\mathcal{E}(X). \end{array}\end{equation*}
  [5] proposed the generalized entropy functional of order α (as a general form of CRE) as follows
  (9)\begin{equation} h_{\alpha}(\bar{F})=-\int_{0}^{\infty}\bar{F}^{\alpha}(x) L_{\alpha}(\bar{F}(x))dx, \quad \alpha \gt 0, \end{equation}

  where

  \begin{align*} L_{\alpha}(x)=\left\{ \begin{array}{ll} \frac{x^{1-\alpha}-1}{1-\alpha} & {x\geq 0, \alpha\in(0,1)\bigcup (1,\infty)} \\ \log x & {x \gt 0, \alpha =1}. \end{array} \right. \end{align*}

  Note that the case $\alpha\rightarrow 1$, results in the CRE in (2). It is easily seen from (7) that $E_{\alpha}(T_X)$ can also be represented in terms of generalized entropy functional as

  \begin{equation*}E_{\alpha}(T_X)= h_{\alpha+1}(\bar{F}).\end{equation*}

  On the other hand, it can be easily shown that for a random variable with reliability function $\bar{F}^{\alpha}(t)$, α > 0, if $m_{\alpha}(t)$ denotes the corresponding MRL, i.e.,

  \begin{equation*}m_{\alpha}(t)=\frac{\int_{t}^{\infty}\bar{F}^{\alpha}(x)dx}{\bar{F}^{\alpha}(t)}\end{equation*}

  then,

  \begin{equation*}h_{\alpha}(\bar{F})={\mathbb{E}}(m_{\alpha}(T)).\end{equation*}

  Thus, another alternative for representing $E_{\alpha}(T_X)$ is as follows

  \begin{equation*} E_{\alpha}(T_X)= {\mathbb{E}}(m_{\alpha+1}(T)).\end{equation*}

• • An actuarial index: [36] introduced an actuarial index which measures the right-tail deviation for a nonnegative random variable T. Denoting the reliability function of T by $\bar{F}$, it is defined as

  \begin{equation*} W(T)=\int_{0}^{\infty}\bar{F}^{\frac{1}{2}}(x)dx -{\mathbb{E}}(T). \end{equation*}

  It is easily seen that for the case that T and X both identically distributed as $\bar{F}^{\frac{1}{2}}(t)$, then we have from (6),

  \begin{align*} {\mathbb{E}}(T_X) &=\frac{\int_{0}^{\infty}\bar{F}^{\frac{1}{2}}(t)(1-\bar{F}^{\frac{1}{2}}(t))dt }{\frac{1}{2}\int_{0}^{\infty}{\bar{F}(x)}dF(x)}\\ &=4W(T).\end{align*}

• • Equilibrium distribution: The equilibrium distribution (ED) corresponding to distribution function F is a distribution with the density function given by

  \begin{equation*} g_e(x)= \frac{\bar{F}(x)}{\mu},\end{equation*}

  where $0 \lt \mu \lt \infty$ is the mean of F. In a renewal process, the ED arises as the asymptotic distribution of the waiting time until the next renewal and the time since the last renewal at time t. Also, a delayed renewal process has stationary increments if and only if the distribution of the actual remaining life is $g_{e}(x)$. Such a process is known in the literature as the stationary renewal process or equilibrium renewal process (see [32]). If we assume that the random age X has an ED with density $g_e(x)$, then ${\mathbb{E}}(T_X)$ is given as

  \begin{align*} {\mathbb{E}}(T_X) &=\frac{\int_{0}^{\infty}{\bar{F}(t)}G(t)dt }{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\[8pt] &= \frac{\int_{0}^{\infty}{\bar{F}(t)}\left(\int_{0}^{t}\bar{F}(x)dx\right)dt }{\int_{0}^{\infty}{\bar{F}^2(x)}dx}\\[8pt] &=\frac{\left(\int_{0}^{\infty}{\bar{F}(t)dt}\right)^2 }{\int_{0}^{\infty}{\bar{F}^2(x)}dx} =\frac{\mu^2 }{\mu_2}, \end{align*}

  where µ ₂ is the expectation of a minimum of a random sample of size 2 from distribution F.

• • Upper record values: The upper record values, in a sequence of i.i.d. random variables $X_1, X_2,...$, have applications in different areas of applied probability and reliability engineering (see [2]). Let X_i’s have a common, absolutely continuous cdf F(t). Define a sequence of record times $U(n), n=1,2,...,$ as follows.

  \begin{equation*}U(n+1)=\min\left\{j:j \gt U(n),\;X_{j} \gt X_{U(n)}\right\},\;\; n\geq1,\end{equation*}

  with $ U(1)=1$. Then, the sequence of upper record values $\{R_n, n\geq1\}$ is defined by $R_n= X_{U(n)}, \ n\geq 1$, where $R_1=X_1$. The reliability function of R_n is given as

  (10)\begin{equation} \bar{F}_{n}(t)=\bar{F}(t)\sum_{x=0}^{n-1}\frac{[-\log \bar{F}(t)]^x}{x!}, \ \quad t \gt 0,\ n=1,2\ldots. \end{equation}

  The upper records can be viewed as the maxima in a sample of random size n, where n is determined by the values and the order of occurrence of the observations. From the reliability theory point of view, the nth record is just the failure time of the 1-out-of-U(n) system. Also, if S_n denotes the occurrence time of the n-th event in a non-homogeneous Poisson process (NHPP) with the mean value function $\Lambda(t)=-\log\bar{F}(t)$, then $R_n\stackrel{d}{=}S_n$, $n=1,2,\ldots,$ where $\stackrel{d}{=}$ denotes equality in distribution; see [18]. It is well-known that the process of minimal repairs (that restores an item to the state it has just before a failure) forms the corresponding NHPP. If we assume that n = 2 in (10), and assume that G(x) in (6) is the distribution of R ₂ then, we obtain

  \begin{align*} {\mathbb{E}}(T_X) &=\frac{\int_{0}^{\infty}{\bar{F}(t)}G(t)dt }{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\[4pt] &= \frac{\int_{0}^{\infty}{\bar{F}(t)}\big(1-\bar{F}(t)+\bar{F}(t)\log\bar{F}(t)\big) }{-\int_{0}^{\infty}f(t)\bar{F}(t)\log\bar{F}(t)}\\[4pt] &= \frac{\int_{0}^{\infty}{\bar{F}(t)}F(t)dt+\frac{1}{2}\int_{0}^{\infty}\bar{F}^2(t)\log\bar{F}^2(t)\big) }{-\int_{0}^{\infty}f(t)\bar{F}(t)\log\bar{F}(t)}\\[4pt] &= 2\big[GMD(T) -\mathcal{E}(T^*)], \end{align*}

  where $T^*$ is a random variable showing the minimum of a random sample with size 2 from F.

  If we assume that T has a distribution as of R ₂, and $G(x)=F(x)$, then

  \begin{align*} {\mathbb{E}}(T_X) &= \frac{\int_{0}^{\infty}{\big(\bar{F}(t)-\bar{F}(t)\log\bar{F}(t)\big)\big(1-\bar{F}(t)\big)} }{\int_{0}^{\infty}\big(\bar{F}(t)-\bar{F}(t)\log\bar{F}(t)\big)f(t)}\\ &=\frac{4}{3}\big[{\mathbb{E}}(R_2-R^*_2)\big], \end{align*}

  where $R^*_2$ is the second upper record value based on a sequence of i.i.d random variables with reliability function $\bar{F}^2$.

• • Finite range distributions: Assume that T is a continuous random variable distributed on a finite set $(0,\tau)$, τ > 0 with distribution function F. Furthermore, assume that X has the power distribution on $(0,\tau)$, i.e., $G(x)=(\frac{x}{\tau})^a$, $0 \lt x \lt \tau$, a > 1. Under these circumstances, we have

  \begin{align*} {\mathbb{E}}(T_X) &=\frac{\int_{0}^{\infty}{\bar{F}(t)}G(t)dt }{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\\ &=\frac{\int_{0}^{\tau}{t^a\bar{F}(t)}dt }{\int_{0}^{\tau}{at^{a-1}\bar{F}(x)}dx}\\ &=\frac{{\mathbb{E}}(T^{a+1})}{(a+1){\mathbb{E}}(T^a)}. \end{align*}

3.2. The MRL and MIT representations of ${\mathbb{E}}(T_X)$

As we already mentioned, the mean remaining lifetime of a non-negative random variable T, denoted by m(t), is defined as

\begin{equation*} m(t)={\mathbb{E}}(T-t|T \gt t)=\frac{\int_{t}^{\infty}{\bar{F}(x)dx}}{\bar{F}(t)}. \end{equation*}

The following simple result shows that ${\mathbb{E}}(T_X)$ can be represented in terms of m(t) (see also [13]).

Proposition 3.8. Assume that m(t) is the MRL of T. Then ${\mathbb{E}}(T_X)$ can be represented as

\begin{equation*} {\mathbb{E}}(T_X)={\mathbb{E}}(m(X)|T \gt X), \end{equation*}

where the expectation on the RHS is over the distribution of the conditional random variable $(X|T \gt X).$

Proof. First note that the conditional distribution of $(X|T \gt X) $ has a density function of the form

\begin{equation*}g^{*}(t)\equiv\frac{\bar{F}(t)dG(t)}{\int_{0}^{\infty}\bar{F}(t)dG(t)}, \quad t \gt 0.\end{equation*}

We have (see also Theorem 3.1 of [21]),

(11)\begin{align} {\mathbb{E}}(T_X)&= \frac{\int_{0}^{\infty}\left(\int_{0}^{\infty}{\bar{F}(t+x)}dG(x)\right)dt}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\nonumber\\ &=\frac{\int_{0}^{\infty}\left(\int_{x}^{\infty}{\bar{F}(t)}dt\right)dG(x)}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\nonumber\\ &=\frac{\int_{0}^{\infty}m(x)\bar{F}(x)dG(x)}{\int_{0}^{\infty}{\bar{F}(x)}dG(x)}\nonumber\\ &={\int_{0}^{\infty}m(x)g^*(x)dx}\nonumber\\ &={\mathbb{E}}(m(X)|T \gt X) \end{align}

The result of the theorem shows that ${\mathbb{E}}(T_X)$ can be represented as the conditional expectation of m(X) given that T > X.

For a system with lifetime random variable X having distribution function G, the MIT of X is defined as

\begin{equation*}k(t)\equiv {\mathbb{E}}(t-X|X \lt t)=\frac{\int_{0}^{t}G(x)dx}{G(t)},\end{equation*}

provided that $G(t) \gt 0$. Assuming that the system has already failed before time t, k(t) shows the mean time of the inactivity of the system until time t. Similar to Proposition 3.8, we have the following proposition.

Proposition 3.9. The MRLR ${\mathbb{E}}(T_X)$ can be represented in terms of MIT of X, k(t), as follows

\begin{equation*} {\mathbb{E}}(T_X)=\frac{\int_{0}^{\infty}k(x)G(x)dF(x)}{\int_{0}^{\infty}{G(x)dF(x)}}={\mathbb{E}}(k(T)|X \lt T), \end{equation*}

where the expectation is over the distribution of the conditional random variable $(T|X \lt T)$ with density

\begin{equation*}h(t)\equiv\frac{G(t)dF(t)}{\int_{0}^{\infty} G(x)dF(x)}.\end{equation*}

As an application of (11), we give the following example.

Example 3.10. Let T belong to the class of generalized Pareto distributions (GPD). Recall that a lifetime random variable T belongs to GPD if its survival function is given by

(12)\begin{equation} \bar{F}(t)=\left(\frac{b}{at+b}\right)^{\frac{1}{a}+1} \qquad t\geq 0, \ a \gt -1, b \gt 0. \end{equation}

This family of distributions, depending on the values of a, includes three distributions:

• • The exponential distribution when $a\rightarrow0$;

• • The Pareto distribution when a > 0;

• • The power distribution when $-1 \lt a \lt 0$. In particular, when $a=-1/2$, the distribution is uniform.

The GPD has a linear MRL of the form $m(t)=at+b$. Using representation (11), we observe that ${\mathbb{E}}(T_X)$ is given by

\begin{equation*} {\mathbb{E}}(T_X) =a{\mathbb{E}}(X|T \gt X)+b. \end{equation*}

Before giving the next results, we recall the definitions of stochastic and hazard rate orders between two random variables (see [33]). Let X(Y) be a random variable with reliability function $\bar{F}$( $\bar{G}$), density function f(g), and hazard rate $r(t)=\frac{f(t)}{\bar{F}(t)}$ ( $q(t)=\frac{g(t)}{\bar{G}(t)}$), respectively.

• • If $\bar{F}(t)\le \bar{G}(t)$ for all $t \in (-\infty,+\infty)$, then X is said to be smaller than Y in the usual stochastic order (denoted by $X \le_{st} Y$ ).

• • If $r(t) \ge q(t),$ for all $t\in \mathbb{R}$ then X is said to be smaller than Y in the hazard rate order (denoted as $X \le_{hr} Y$).

The following lemma from Asadi and Shanbhag [7] is useful in the next proposition.

Lemma 3.11. Let X and Y be two random variables such that $X\leq_{hr} Y$ and Z be a continuous random variable independent of X and Y such that $P(Y \gt Z) \gt 0$ (and hence also such that $P(X \gt Z) \gt 0$). Then $(X|X \gt Z)\leq_{st} (Y| Y \gt Z)$.

From the result of this lemma, we get the following proposition.

Proposition 3.12. Let T₁ and T₂ be two random lifetimes with random age X such that $T_1\leq_{hr} T_2$. Let k(t) be the MIT of X such that k(t) is increasing. Then ${\mathbb{E}}(T_{1X})\leq {\mathbb{E}}(T_{2X})$, where T_iX is the remaining lifetime for the lifetime T_i, $i=1,2$.

Proof. We use the fact that for two random variables W ₁ and W ₂, $W_1\leq_{st}W_2$ is equivalent to ${\mathbb{E}}(\eta(W_1))\leq {\mathbb{E}}(\eta(W_2))$ for any increasing function η. Based on this fact, we have

\begin{align*} {\mathbb{E}}(T_{1X})&= \frac{\int_{0}^{\infty}k(x)G(x)dF_1(x)}{\int_{0}^{\infty}{G(x)dF_1(x)}}\\ &\leq \frac{\int_{0}^{\infty}k(x)G(x)dF_2(x)}{\int_{0}^{\infty}{G(x)dF_2(x)}}\\ &={\mathbb{E}}(T_{2X}), \end{align*}

where the inequality follows from the assumption that k(t) is assumed to be increasing and Lemma 3.11 under which the condition $T_1\leq_{hr} T_2$ implies that $(T_1|T_1 \gt X)\leq_{st}(T_2|T_2 \gt X)$.

The following proposition can be proved using a modified version of Lemma 3.11 which we omit the details of the proof.

Proposition 3.13. Let T be a random lifetime and consider two random ages X₁ and X₂ such that $X_1\leq_{hr} X_2$. Let m(t) be the MRL of T such that m(t) is increasing. Then ${\mathbb{E}}(T_{1X})\leq {\mathbb{E}}(T_{2X})$, where T_iX is the remaining lifetime for the lifetime T_i, $i=1,2$.

4. Decomposition of the MRLR

This section gives a decomposition theorem regarding the MRLR ${\mathbb{E}}(T_X)$. In what follows, we assume that all integrals exist. We have the following theorem.

Theorem 4.1. The expectation ${\mathbb{E}}(T_X)$ can be decomposed as

(13)\begin{equation} {\mathbb{E}}(T_X) ={\rm Cov}\left(T,G^*(T)\right)+ {\rm Cov}\left(X,F^*(X)\right)+{\mathbb{E}}(T-X), \end{equation}

where $G^*(T)=\frac{G(T)}{{\mathbb{E}}(G(T))}$ and $F^*(X)=\frac{F(X)}{{\mathbb{E}}(\bar{F}(X))}.$

Proof. Using integration by parts, we have

(14)\begin{align} \int_{0}^{\infty}{\bar{F}(t)}G(t)dt&=\int_{0}^{\infty}tG(t)dF(t)-\int_{0}^{\infty}t\bar{F}(t)dG(t)\nonumber\\ &=E\left[TG(T)\right]-E\left[X\bar{F}(X)\right]\nonumber\\ &={\rm Cov}(T,G(T))+{\rm Cov}(X,{F}(X))+{\mathbb{E}}(T){\mathbb{E}}(G(T))-{\mathbb{E}}(X){\mathbb{E}}(\bar{F}(X)). \end{align}

Using the fact that

\begin{equation*}\int_{0}^{\infty}{\bar{F}(x)}dG(x)={\mathbb{E}}(\bar{F}(X))={\mathbb{E}}(G(T)),\end{equation*}

from (6) and (14) we arrive at the decomposition in (13).

Representation (13) may be interpreted as follows. The MRL ${\mathbb{E}}(T_X)$ can be decomposed into two non-negative parts: one is the difference between the means of lifetime random variable T and random age X and the other one is the sum of covariance between lifetime T and G(T) and the covariance between X and F(X).

The next corollaries immediately follow from this theorem.

Corollary 4.2. In the particular case that $T\stackrel{d}{=}X$, since $E(F(T))=\frac{1}{2}$, the covariance representation (13) reduces to covariance representation of GMD.

\begin{equation*}\begin{array}{ll} {\mathbb{E}}(T_X) &={\rm Cov}\left(T,G^*(T)\right)+ {\rm Cov}\left(X,F^*(X)\right)+{\mathbb{E}}(T-X)\\ &= 2{\rm Cov}\left(T,F(T)\right)+ 2{\rm Cov}\left(X,F(T)\right)\\ &=4{\rm Cov}\left(T,F(T)\right)\!. \end{array}\end{equation*}

It is easy to see that, in the case when $\bar{G}(t)=\bar{F}^{\alpha}(t)$, Eq. (14) results in the covariance representation of extended GMD.

Corollary 4.3. As F and G are both non-decreasing functions the covariances in (13) are both nonnegative and thus we have ${\mathbb{E}}(T_X)\geq {\mathbb{E}}(T-X)$.

Corollary 4.4. As an application of Cauchy-Schwartz inequality, we obtain the following inequality.

(15)\begin{align} {\mathbb{E}}(T_X) &={\rm Cov}\left(T,G(T)\right)+ {\rm Cov}\left(X,F(X)\right)+{\mathbb{E}}(T-X)\nonumber\\ &\leq [\sigma_T\sigma_{G^*(T)}+\sigma_X\sigma_{F^*(X)}]+{\mathbb{E}}(T-X)\nonumber\\ &\leq \frac{\sigma_T+\sigma_X}{a}+{\mathbb{E}}(T-X) \end{align}

where $a=E(G(T))$, $\sigma_{T}(\sigma_X)$ denotes the standard deviation of $T(X)$, and $\sigma_{G(T)}$ $(\sigma_{F(X)})$ is the standard deviation of G(T) $(F(X))$.

From the results of Corollaries 4.3 and 4.4, we conclude that, ${\mathbb{E}}(T_X)$ is bounded as follows:

\begin{equation*} {\mathbb{E}}(T-X)\leq {\mathbb{E}}(T_X) \leq \frac{\sigma_T+\sigma_X}{a}+{\mathbb{E}}(T-X). \end{equation*}

5. MRL in random age: dependent case

Although we have assumed that T and X are independent, in practical situations these may be dependent. In order to model the dependency between two random variables, the copula function has proved to be a very flexible tool independent of their marginal behavior. For more information on the concept of copula and its applications, we refer to the monographs by Nelsen [29]. In a recent paper, Navvaro and Sarabia [28] studied the copula representations for the sum of random variables.

A two-dimensional copula is a bivariate distribution function whose marginal distributions are uniform on $(0, 1)$. The importance of copulas is described in Sklar’s theorem which proves how copulas link joint distribution functions to their one-dimensional marginlas. In fact, according to Sklar’s theorem, any bivariate distribution $H(x, y)$ of variables T and X, with marginal distributions F(x) and G(y), can be written as $H(x, y) = C(F(x), G(y))$, where C is a copula. Thus, any copula and any two marginal distributions result in the construction of a bivariate distribution. Analogously, the bivariate survival function of T and X with marginal survival functions $\bar{F}(x)$ and $\bar{G}(x)$ can be written in terms of bivariate survival copula as $\bar{H}(x, y) = \bar{C}(\bar{F}(x), \bar{G}(y))$, where $\bar{C}$ is a bivariate survival function whose marginals are uniformly distributed on $(0,1)$. According to the definition, we have

\begin{equation*}\bar{C}(u, v)=u+v-1+C(1-u,1-v).\end{equation*}

Assume that T and X are dependent random variables with survival functions $\bar{F}$ and $\bar{G}$, respectively. In this case, the reliability function of T_X can be written as follows:

(16)\begin{align} P(T_{X} \gt t)&=P(T-X \gt t|T \gt X)\nonumber\\ &=\frac{\int_{0}^{\infty}P(T \gt x+t|X=x)dG(x)}{\int_{0}^{\infty}{P(T \gt x|X=x)}dG(x)}. \end{align}

Furthermore, let the dependency between T and X is characterized by joint survival copula $\bar{C}(\bar{F}(x),\bar{G}(x))$. Then it can be easily shown that (see [23])

\begin{equation*}P(T \gt x+t|X=x)=\frac{\partial}{\partial v} \bar{C}(\bar{F}(x+t),\bar{G}(x)),\end{equation*}

where $\frac{\partial}{\partial v} \bar{C}(u,v)$ is the partial derivative of the survival copula in terms of v. Thus, substituting the RHS of this last equality in (16), we get

\begin{align*} P(T_{X} \gt t)&=P(T-X \gt t|T \gt X)\\[4pt] &=\frac{\int_{0}^{\infty}\frac{\partial}{\partial v} \bar{C}(\bar{F}(x+t),\bar{G}(x))dG(x)}{\int_{0}^{\infty}{\frac{\partial}{\partial v} \bar{C}(\bar{F}(x),\bar{G}(x))}dG(x)}. \end{align*}

From this, we get

(17)\begin{align} {\mathbb{E}}(T_X)&=\int_{0}^{\infty}P(T_{X} \gt t)dt\nonumber\\[4pt] &=\frac{\int_{0}^{\infty}\left(\int_{0}^{\infty}\frac{\partial}{\partial v} \bar{C}(\bar{F}(x+t),\bar{G}(x))dG(x)\right)dt}{\int_{0}^{\infty}{\frac{\partial}{\partial v} \bar{C}(\bar{F}(x),\bar{G}(x))}dG(x)}\nonumber\\[4pt] &=\frac{\int_{0}^{\infty}\left(\int_{x}^{\infty}\frac{\partial}{\partial v} \bar{C}(\bar{F}(t),\bar{G}(x))dt\right)dG(x)}{\int_{0}^{\infty}{\frac{\partial}{\partial v} \bar{C}(\bar{F}(x),\bar{G}(x))}dG(x)}\nonumber\\[4pt] &=\frac{\int_{0}^{\infty}\left(\int_{0}^{t}\frac{\partial}{\partial v} \bar{C}(\bar{F}(t),\bar{G}(x))dG(x)\right)dt}{\int_{0}^{\infty}{\frac{\partial}{\partial v} \bar{C}(\bar{F}(x),\bar{G}(x))}dG(x)}\nonumber\\[4pt] &=\frac{\int_{0}^{\infty}\left(\bar{F}(t)-\bar{C}(\bar{F}(t),\bar{G}(t))\right)dt}{\int_{0}^{\infty}{\frac{\partial}{\partial v} \bar{C}(\bar{F}(x),\bar{G}(x))}dG(x)}\nonumber\\[4pt] &=\frac{\int_{0}^{\infty}\bar{F}(t)dt-\int_{0}^{\infty}\bar{C}(\bar{F}(t),\bar{G}(t))dt}{\int_{0}^{\infty}{\frac{\partial}{\partial v} \bar{C}(\bar{F}(x),\bar{G}(x))}dG(x)}. \end{align}

In particular case that T and X are independent, we have $\bar{C}(\bar{F}(t),\bar{G}(t))=\bar{F}(t)\bar{G}(t)$ and thus $\frac{\partial}{\partial v} \bar{C}(\bar{F}(x),\bar{G}(x))=\bar{F}(t)$. This implies that, ${\mathbb{E}}(T_X)$ in (17) reduces to the MRLR ${\mathbb{E}}(T_X)$ in (6).

As an example let T and X have a joint distribution that follows the Ali-Mikhail-Haq survival copula with the joint survival function

\begin{equation*} \bar{H}(x,y)=\bar{C}(\bar{F}(x),\bar{G}(x))=\frac{\bar{F}(x)\bar{G}(y)}{1-\alpha{F}(x){G}(y)}, \qquad x,y \gt 0,\ \alpha\in[-1,1].\end{equation*}

Then, simple calculations show that

\begin{align*} {\mathbb{E}}(T_X) &=\frac{\int_{0}^{\infty}\bar{F}(t)dt-\int_{0}^{\infty}\bar{C}(\bar{F}(t),\bar{G}(t))dt}{\int_{0}^{\infty}{\frac{\partial}{\partial v} \bar{C}(\bar{F}(x),\bar{G}(x))}dG(x)}\\ &=\frac{\int_{0}^{\infty}\phi_{1}(t)\bar{F}(t){G}(t)dt}{\int_{0}^{\infty}\phi_{2}(t)\bar{F}(t)dG(x)}, \end{align*}

where $\phi_{1}(x)=\frac{1-\alpha F(x)}{1-\alpha F(x)G(x)}$ and $\phi_{2}(x)=\frac{1-\alpha F(x)}{[1-\alpha F(x)G(x)]^2}$. Trivially, for the case that T and X are independent (that is, α = 0) we have $\phi_{1}(x)=\phi_{2}(x)=1$, and hence we arrive at the MRLR in the independent case.

6. Concluding remarks

In this paper, we investigated the MRL of a non-negative random variable T at a random age X (MRLR). The results unveiled that there is a significant relationship between the MRLR and several well-established measures of variability. In particular, the MRLR can be considered an extension of GMD. Under the proportional hazards model, we demonstrated how the MRLR encompasses both the extended GMD and the extended CRE as special cases. It is also shown that the MRLR can be represented as the conditional expectation of the ordinary MRL of T and the expectation of the MIT of X. Furthermore, we presented a decomposition result revealing that the MRLR can be decomposed into two covariance functionals and the difference between the means of lifetime T and the random age X. Additionally, we established some stochastic comparison results between the MRLs of two systems at random ages. Finally, we considered the case that T and X are dependent. Under this condition, we have given the formula for $E(T_X)$ in the case where a copula function characterizes the dependency structure between T and X. Assessing the several properties of $E(T_X)$ and its possible connections to variability measures in the dependent are promising problems that need further investigation which we leave for future study.