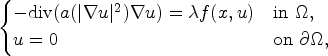1 results
Existence of solution for quasilinear equations involving local conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3074-3086
- Print publication:
- December 2020
-
- Article
- Export citation
-
In this paper, we study the existence of weak solutions of the quasilinear equation
where a : ℝ → [0, ∞) is C1 and a nonincreasing continuous function near the origin, the nonlinear term f : Ω × ℝ → ℝ is a Carathéodory function verifying certain superlinear conditions only at zero, and λ is a positive parameter. The existence of the solution relies on C1-estimates and variational arguments.
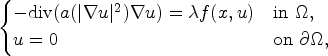\begin{cases} -{\rm div} (a(\vert \nabla u \vert ^2)\nabla u)=\lambda f(x,u) &{\rm in} \ \Omega,\\ u=0 &{\rm on} \ \partial\Omega, \end{cases}
