No CrossRef data available.
Published online by Cambridge University Press: 17 September 2019
In this paper, we study the existence of weak solutions of the quasilinear equation
where a : ℝ → [0, ∞) is C1 and a nonincreasing continuous function near the origin, the nonlinear term f : Ω × ℝ → ℝ is a Carathéodory function verifying certain superlinear conditions only at zero, and λ is a positive parameter. The existence of the solution relies on C1-estimates and variational arguments.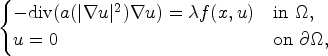 \begin{cases} -{\rm div} (a(\vert \nabla u \vert ^2)\nabla u)=\lambda f(x,u) &{\rm in} \ \Omega,\\ u=0 &{\rm on} \ \partial\Omega, \end{cases}
\begin{cases} -{\rm div} (a(\vert \nabla u \vert ^2)\nabla u)=\lambda f(x,u) &{\rm in} \ \Omega,\\ u=0 &{\rm on} \ \partial\Omega, \end{cases}