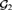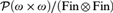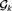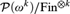2 results
STRUCTURAL CONSIDERATIONS OF RAMSEY ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1677-1692
- Print publication:
- December 2022
-
- Article
- Export citation
HIGH DIMENSIONAL ELLENTUCK SPACES AND INITIAL CHAINS IN THE TUKEY STRUCTURE OF NON-P-POINTS
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 09 March 2016, pp. 237-263
- Print publication:
- March 2016
-
- Article
- Export citation