1 results
On the number of leaves of a euclidean minimal spanning tree
-
- Journal:
- Journal of Applied Probability / Volume 24 / Issue 4 / December 1987
- Published online by Cambridge University Press:
- 14 July 2016, pp. 809-826
- Print publication:
- December 1987
-
- Article
- Export citation
-
Let Vk,n be the number of vertices of degree k in the Euclidean minimal spanning tree of Xi,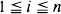
, where the Xi are independent, absolutely continuous random variables with values in Rd. It is proved that n–1Vk,n converges with probability 1 to a constant α k,d. Intermediate results provide information about how the vertex degrees of a minimal spanning tree change as points are added or deleted, about the decomposition of minimal spanning trees into probabilistically similar trees, and about the mean and variance of Vk,n.
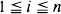, where the 