Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T12:04:30.789Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of leaves of a euclidean minimal spanning tree

Published online by Cambridge University Press:  14 July 2016

J. Michael Steele ,
Lawrence A. Shepp  and
William F. Eddy
J. Michael Steele*
Affiliation:
Princeton University
Lawrence A. Shepp*
Affiliation:
AT&T Bell Laboratories
William F. Eddy*
Affiliation:
Carnegie-Mellon University
*
∗Postal address: Program in Engineering Statistics, Princeton University, Princeton, NJ 08544, USA.
∗∗Postal address: AT&T Bell Laboratories, Murray Hill, NJ 07974, USA.
∗∗∗Postal address: Department of Statistics, Carnegie-Mellon University, Pittsburgh, PA 15213, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

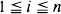Let Vk,n be the number of vertices of degree k in the Euclidean minimal spanning tree of Xi, , where the Xi are independent, absolutely continuous random variables with values in Rd. It is proved that n–1Vk,n converges with probability 1 to a constant α k,d. Intermediate results provide information about how the vertex degrees of a minimal spanning tree change as points are added or deleted, about the decomposition of minimal spanning trees into probabilistically similar trees, and about the mean and variance of Vk,n.

Keywords

SUBADDITIVE EUCLIDEAN FUNCTIONALSVERTEX DEGREESSELF-SIMILAR PROCESSESEFRON–STEIN INEQUALITY
Type
Research Papers
Information
Journal of Applied Probability , Volume 24 , Issue 4 , December 1987 , pp. 809 - 826
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by National Science Foundation Grant DMS-8414069.

References

Beardwood, J., Halton, J. H., and Hammersley, J. M. (1959) The shortest path through many points. Proc. Camb. Phil. Soc. 55, 299–327.CrossRefGoogle Scholar
Bentley, J. L. (1978) Fast algorithms for constructing minimal spanning trees in coordinate spaces. IEEE Comput. 27, 97–105.Google Scholar
Bingham, N. H. (1981) Tauberian theorems and the central limit theorem. Ann. Prob. 9, 221–231.CrossRefGoogle Scholar
De Bruijn, N. D. (1961) Asymptotic Methods in Analysis , 2nd edn. Wiley Interscience, New York.Google Scholar
Chin, F. (1978) Algorithms for updating minimal spanning trees. J. Comput. Syst. 16, 333–344.Google Scholar
Efron, B. and Stein, C. (1981) The jackknife estimate of variance. Ann. Statist. 9, 586–596.CrossRefGoogle Scholar
Friedman, J. H. and Rafsky, L. C. (1979) Multivariate generalizations of the Wolfowitz and Smirnov two-sample tests. Ann. Statist. 7, 697–717.Google Scholar
Hilbert, D. and Cohn-Vossen, S. (1952) Geometry and the Imagination. Chelsea, New York.Google Scholar
Hochbaum, D. and Steele, J. M. (1982) Steinhaus' geometric location problem for random samples in the plane. Adv. Appl. Prob. 14, 55–67.CrossRefGoogle Scholar
Hughes, B. D., Montroll, B. W., and Shlesinger, M. F. (1982) Fractal random walks. J. Statist. Phys. 28, 111–128.CrossRefGoogle Scholar
Jung, H. A. (1974) Determination of minimal paths and spanning trees in graphs. Computing 13, 249.CrossRefGoogle Scholar
Kang, A. N. C. (1977) Storage reduction through minimal spanning trees and spanning forests. IEEE Comput. 26, 425–434.CrossRefGoogle Scholar
Katajainen, J. (1983) On the worst case of a minimal spanning tree algorithm for Euclidean space. BIT 23, 2–8.Google Scholar
Mallion, R. B. (1975) Number of spanning trees in a molecular graph. Chem. Phys. Lett. 36, 170–174.CrossRefGoogle Scholar
Mandelbrot, B. B. (1977) Fractals, Form, Chance, and Dimension. W. H. Freeman, San Francisco.Google Scholar
Najock, D. and Heyde, C. C. (1982) On the number of terminal vertices in certain random trees with an application to stemma construction in philology. J. Appl. Prob. 19, 675–680.Google Scholar
Penny, D. (1980) Techniques for the verification of minimal phylogenetic trees illustrated with 10 mammalian hemoglobin sequences. Biochem. J. 187, 65–74.CrossRefGoogle Scholar
Prodinger, H. (1986) The average height of the d-th highest leaf of a planted tree. Networks 16, 67–75.CrossRefGoogle Scholar
Pynn, C. (1972) Improved algorithm for construction of minimal spanning trees. Elect. Lett. 8, 143.CrossRefGoogle Scholar
Renyi, A. (1959) Some remarks on the theory of random trees. MTA Mat. Ket. Imt. Kozl. 4, 73–85 (also Selected Papers of Alfréd Rényi, Akadémiai Kaidó, Budapest).Google Scholar
Roberts, F. D. K. (1968) Random minimal trees. Biometrika 55, 255–258.CrossRefGoogle Scholar
Roberts, F. D. K. (1969) Nearest neighbors in a Poisson ensemble. Biometrika 54, 401–406.CrossRefGoogle Scholar
Rogers, C. A. (1964) Packing and Covering. Cambridge University Press, Cambridge.Google Scholar
Romane, F. (1977) Possible use of minimum spanning tree in phytoecology. Vegetation 33, 99–106.Google Scholar
Schmidt, R. (1925) Über das Borelsche Summierungsverfahren. Schriften d. Königsberger gel. Gesellschaft 1, 205–256.Google Scholar
Steele, J. M. (1981a) Subadditive Euclidean functionals and non-linear growth in geometric probability. Ann. Prob. 9, 365–376.Google Scholar
Steele, J. M. (1981b) Complete convergence of short paths and Karp's algorithm for the TSP. Math. Operat. Res. 6, 374–378.Google Scholar
Strassen, V. (1965) The existence of probability measures with given marginals. Ann. Math. Statist. 36, 423–439.CrossRefGoogle Scholar
Wald, A. and Wolfowitz, J. (1940) On a test whether two-samples are from the same population. Ann. Math. Statist. 11, 147–162.CrossRefGoogle Scholar
Whitney, V. K. M. (1972) Minimal spanning tree. Comm. ACM 15, 273.CrossRefGoogle Scholar
Wu, F. Y. (1977) Number of spanning trees on a lattice. J. Phys. A 10, L113–L115.CrossRefGoogle Scholar