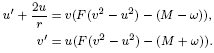2 results
Nonlinear Dirac equations with Coulomb-type potentials and nonlinearities resonating at essential spectrums
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 15 April 2018, pp. 713-730
- Print publication:
- August 2018
-
- Article
- Export citation
-
We consider the nonlinear Dirac equation
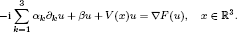
The potential function V satisfies the conditions that the essential spectrum of the Dirac operator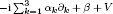
is 
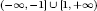and this Dirac operator has infinitely many eigenvalues in (−1, 1) accumulating at 1. This potential function V may change sign in ℝ3 and contains the classical Coulomb potential V (x) = −γ/|x| with γ > 0 as a special case. The nonlinearity F satisfies the resonance-type condition lim
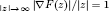. Under some additional conditions on V and F, we prove that this equation has infinitely many solutions.
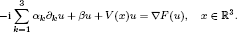
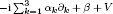is 
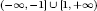and this Dirac operator has infinitely many eigenvalues in (
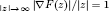. Under some additional conditions on Admissible solutions for Dirac equations with singular and non-monotone nonlinearity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 25 February 2011, pp. 363-371
-
- Article
-
- You have access
- Export citation
-
By making use of Merle's general shooting method we investigate Dirac equations of the form
Here it is possible that F(0) = −∞ and that F(s) defined on (0,+∞) is not monotonously nondecreasing. Our results cover some known ones as a special case.
