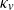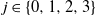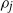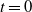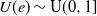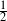2 results
Exponential decay for constrained-degree percolation
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation
Bounding basic characteristics of spatial epidemics with a new percolation model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 335-347
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation