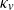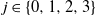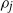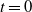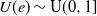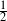1. Introduction
Let
![]() $\mathbb{L}^2=(\mathbb{Z}^2,\mathcal{E})$
be the usual square lattice. With each site
$\mathbb{L}^2=(\mathbb{Z}^2,\mathcal{E})$
be the usual square lattice. With each site
![]() $v\in\mathbb{Z}^2$
we independently associate a random variable
$v\in\mathbb{Z}^2$
we independently associate a random variable
![]() $\kappa_v$
, which takes the value
$\kappa_v$
, which takes the value
![]() $j\in\{0,1,2,3\}$
with probability
$j\in\{0,1,2,3\}$
with probability
![]() $\rho_j$
. Denote by
$\rho_j$
. Denote by
![]() $\mathbb{P}_{\rho}$
the corresponding product measure on
$\mathbb{P}_{\rho}$
the corresponding product measure on
![]() $\{0,1,2,3\}^{{\mathbb{Z}}^2}$
. Consider the following dependent continuous-time percolation process: let
$\{0,1,2,3\}^{{\mathbb{Z}}^2}$
. Consider the following dependent continuous-time percolation process: let
![]() $\{U(e)\}_{e\in\mathcal{E}}$
be a collection of independent and identically distributed random variables with uniform distribution on the interval (0,1]. At time
$\{U(e)\}_{e\in\mathcal{E}}$
be a collection of independent and identically distributed random variables with uniform distribution on the interval (0,1]. At time
![]() $t=0$
, all edges are closed; each edge
$t=0$
, all edges are closed; each edge
![]() $e=\langle u,v\rangle$
opens at time U(e) if
$e=\langle u,v\rangle$
opens at time U(e) if
![]() $|\{z\in\mathbb{Z}^2-\{u\}\colon \langle z,u\rangle\mbox{ is open at time }U(e)\}| < \kappa_{u}$
and
$|\{z\in\mathbb{Z}^2-\{u\}\colon \langle z,u\rangle\mbox{ is open at time }U(e)\}| < \kappa_{u}$
and
![]() $|\{z\in\mathbb{Z}^2-\{v\}\colon \langle z,v\rangle\mbox{ is open at time }U(e)\}| < \kappa_{v}$
. In words, at the random time U(e), the edge e attempts to open. It succeeds if both its endpoints have degrees smaller than their respective attached constraints. Once an edge is open, it remains open.
$|\{z\in\mathbb{Z}^2-\{v\}\colon \langle z,v\rangle\mbox{ is open at time }U(e)\}| < \kappa_{v}$
. In words, at the random time U(e), the edge e attempts to open. It succeeds if both its endpoints have degrees smaller than their respective attached constraints. Once an edge is open, it remains open.
The model described above draws inspiration from the deterministic constraint version introduced in [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5]. In the deterministic model, constraints are fixed to a constant value
![]() $\kappa$
for every vertex. The authors of [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5] proved a non-trivial phase transition for the model on
$\kappa$
for every vertex. The authors of [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5] proved a non-trivial phase transition for the model on
![]() $\mathbb{L}^2$
when
$\mathbb{L}^2$
when
![]() $\kappa=3$
. In contrast, they showed an absence of percolation when
$\kappa=3$
. In contrast, they showed an absence of percolation when
![]() $\kappa=2$
, even at time
$\kappa=2$
, even at time
![]() $t=1$
. In a recent paper, see [Reference Hartarsky and de Lima11], the authors extended some of the results of [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5], proving a phase transition for the model on
$t=1$
. In a recent paper, see [Reference Hartarsky and de Lima11], the authors extended some of the results of [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5], proving a phase transition for the model on
![]() $\mathbb{L}^d$
,
$\mathbb{L}^d$
,
![]() $d\geq 2$
, for several values of a deterministic constant
$d\geq 2$
, for several values of a deterministic constant
![]() $\kappa$
. See [Reference Garet, Marchand and Marcovici8–Reference Grimmett and Li10, Reference Li13] for other models with some type of constraint.
$\kappa$
. See [Reference Garet, Marchand and Marcovici8–Reference Grimmett and Li10, Reference Li13] for other models with some type of constraint.
The random constraint version we approach in this work was initially introduced in [Reference Sanchis, dos Santos and Silva15]. In that work, the authors showed a non-trivial phase transition for the model on
![]() $\mathbb{L}^2$
when
$\mathbb{L}^2$
when
![]() $\rho_3$
is sufficiently large, thus extending the main result of [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5].
$\rho_3$
is sufficiently large, thus extending the main result of [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5].
A formal definition of the constrained-degree percolation model in a random environment (CDPRE) model reads as follows. To each edge
![]() $e\in\mathcal{E}$
, we independently assign a random variable
$e\in\mathcal{E}$
, we independently assign a random variable
![]() $U(e) \sim \mathrm{U}(0,1]$
, independent of
$U(e) \sim \mathrm{U}(0,1]$
, independent of
![]() $\{\kappa_v\}_{v\in{\mathbb{Z}}^2}$
. The corresponding product measure is denoted by
$\{\kappa_v\}_{v\in{\mathbb{Z}}^2}$
. The corresponding product measure is denoted by
![]() $\mathbb{P}$
. We think of U(e) as the time when edge e attempts to open and usually refer to
$\mathbb{P}$
. We think of U(e) as the time when edge e attempts to open and usually refer to
![]() $\{U(e)\}_{e\in\mathcal{E}}$
as a configuration of clocks. Given a collection of constraints
$\{U(e)\}_{e\in\mathcal{E}}$
as a configuration of clocks. Given a collection of constraints
![]() $\kappa=\{\kappa_v\}_{v\in\mathbb{Z}^2}$
and a clock configuration
$\kappa=\{\kappa_v\}_{v\in\mathbb{Z}^2}$
and a clock configuration
![]() $U=\{U(e)\}_{e\in\mathcal{E}}$
, let
$U=\{U(e)\}_{e\in\mathcal{E}}$
, let
![]() $\omega_t\colon\{0,1,2,3\}^{{\mathbb{Z}}^2}\times[0,1]^{\mathcal{E}}\rightarrow\{0,1\}^{\mathcal{E}}$
be the function that associates the pair
$\omega_t\colon\{0,1,2,3\}^{{\mathbb{Z}}^2}\times[0,1]^{\mathcal{E}}\rightarrow\{0,1\}^{\mathcal{E}}$
be the function that associates the pair
![]() $(\kappa,U)$
with a configuration
$(\kappa,U)$
with a configuration
![]() $\omega_t(\kappa,U)$
of open and closed edges at time t. From now on, we use the short notation
$\omega_t(\kappa,U)$
of open and closed edges at time t. From now on, we use the short notation
![]() $\omega_t$
and denote by
$\omega_t$
and denote by
![]() $\omega_{t,e}$
the status of the edge e in the configuration
$\omega_{t,e}$
the status of the edge e in the configuration
![]() $\omega_t$
. We say an edge e is t-open (t-closed) if
$\omega_t$
. We say an edge e is t-open (t-closed) if
![]() $\omega_{t,e}=1$
(
$\omega_{t,e}=1$
(
![]() $\omega_{t,e}=0$
). Formally, writing
$\omega_{t,e}=0$
). Formally, writing
![]() $\textbf{1}\{A\}$
for the indicator function of the event A and
$\textbf{1}\{A\}$
for the indicator function of the event A and
![]() $\mathrm{deg}(v,t)$
for the degree of vertex v in
$\mathrm{deg}(v,t)$
for the degree of vertex v in
![]() $\omega_t$
, the configuration at edge
$\omega_t$
, the configuration at edge
![]() $e=\langle u,v \rangle$
is written as
$e=\langle u,v \rangle$
is written as
Using Harris’s construction, it is straightforward to show that
![]() $\omega_t$
is well defined for almost all sequences
$\omega_t$
is well defined for almost all sequences
![]() $U=\{U(e)\}_{e\in\mathcal{E}}$
and
$U=\{U(e)\}_{e\in\mathcal{E}}$
and
![]() $\kappa=\{\kappa_v\}_{v\in\mathbb{Z}^2}$
and all
$\kappa=\{\kappa_v\}_{v\in\mathbb{Z}^2}$
and all
![]() $t\in[0,1]$
; see the discussion after [Reference Sanchis, dos Santos and Silva15, Theorem 2].
$t\in[0,1]$
; see the discussion after [Reference Sanchis, dos Santos and Silva15, Theorem 2].
Denote by
![]() $\mathbb{P}_{\rho,t}$
the pushforward product law governing
$\mathbb{P}_{\rho,t}$
the pushforward product law governing
![]() $\omega_t$
, that is, for any measurable set
$\omega_t$
, that is, for any measurable set
![]() $A\subset\{0,1\}^{\mathcal{E}}$
,
$A\subset\{0,1\}^{\mathcal{E}}$
,
![]() $\mathbb{P}_{\rho,t}(A)=(\mathbb{P}_{\rho}\times \mathbb{P})(\omega_t^{-1}(A))$
.
$\mathbb{P}_{\rho,t}(A)=(\mathbb{P}_{\rho}\times \mathbb{P})(\omega_t^{-1}(A))$
.
What makes this model interesting is that, at any fixed time
![]() $t>0$
, the configurations exhibit infinite-range dependencies. However, as we will show later, the dependence between the states of any two edges decays at least exponentially as the distance between them increases (see Proposition 1 in Section 2.1), a fact that will be important in this work.
$t>0$
, the configurations exhibit infinite-range dependencies. However, as we will show later, the dependence between the states of any two edges decays at least exponentially as the distance between them increases (see Proposition 1 in Section 2.1), a fact that will be important in this work.
Remark 1. We stress that the model lacks the Fortuin–Kasteleyn–Ginibre (FKG) property, which makes the analysis significantly harder. For instance, consider
![]() $\rho_3=1$
and
$\rho_3=1$
and
![]() $t>0$
. Then, the probability that all four edges incident to some vertex v are open at time t vanishes, while the probability that any pair of such edges are open at time t remains strictly positive.
$t>0$
. Then, the probability that all four edges incident to some vertex v are open at time t vanishes, while the probability that any pair of such edges are open at time t remains strictly positive.
1.1. Results and discussion
Before we state our results, let us introduce some notation. A path of
![]() $\mathbb{L}^2$
is an alternating sequence
$\mathbb{L}^2$
is an alternating sequence
![]() $v_0,e_0,v_1,e_1,\dots,e_{n-1},v_n$
of distinct vertices
$v_0,e_0,v_1,e_1,\dots,e_{n-1},v_n$
of distinct vertices
![]() $v_j$
and edges
$v_j$
and edges
![]() $e_j=\langle v_j,v_{j+1}\rangle$
. Such a path has length n and is said to connect
$e_j=\langle v_j,v_{j+1}\rangle$
. Such a path has length n and is said to connect
![]() $v_0$
to
$v_0$
to
![]() $v_n$
. A path is said to be open if all of its edges are open. Write
$v_n$
. A path is said to be open if all of its edges are open. Write
![]() $C_v$
for the open cluster of
$C_v$
for the open cluster of
![]() $v\in{\mathbb{Z}}^2$
, i.e. the set of vertices connected to v by an open path. By translation invariance of the probability measure, we take this vertex to be the origin and define the percolation and susceptibility critical thresholds
$v\in{\mathbb{Z}}^2$
, i.e. the set of vertices connected to v by an open path. By translation invariance of the probability measure, we take this vertex to be the origin and define the percolation and susceptibility critical thresholds
respectively. Here,
![]() $\mathbb{E}_{\rho,t}$
denotes expectation with respect to
$\mathbb{E}_{\rho,t}$
denotes expectation with respect to
![]() $\mathbb{P}_{\rho,t}$
. Clearly,
$\mathbb{P}_{\rho,t}$
. Clearly,
![]() $\bar{t}_\mathrm{c}(\rho)\leq t_\mathrm{c}(\rho)$
.
$\bar{t}_\mathrm{c}(\rho)\leq t_\mathrm{c}(\rho)$
.
Let
![]() $u,v\in\mathbb{Z}^2$
and denote by d(u,v) the graph distance between u and v. Write
$u,v\in\mathbb{Z}^2$
and denote by d(u,v) the graph distance between u and v. Write
![]() $B(n)=[-n,n]^2$
for the box of side length 2n centered at the origin. For
$B(n)=[-n,n]^2$
for the box of side length 2n centered at the origin. For
![]() $x\in{\mathbb{Z}}^2$
, we define
$x\in{\mathbb{Z}}^2$
, we define
![]() $B(x,n)=x+B(n)$
. Given
$B(x,n)=x+B(n)$
. Given
![]() $\Gamma\subset{\mathbb{Z}}^2$
, we write
$\Gamma\subset{\mathbb{Z}}^2$
, we write
![]() $\mathcal{E}(\Gamma)$
to denote the set of edges with both endpoints in
$\mathcal{E}(\Gamma)$
to denote the set of edges with both endpoints in
![]() $\Gamma$
. We use
$\Gamma$
. We use
![]() $\partial \Gamma$
to denote the vertex boundary of
$\partial \Gamma$
to denote the vertex boundary of
![]() $\Gamma$
, being the set of vertices in
$\Gamma$
, being the set of vertices in
![]() $\Gamma$
which are adjacent to some vertex not in
$\Gamma$
which are adjacent to some vertex not in
![]() $\Gamma$
. We also write
$\Gamma$
. We also write
![]() $\partial^\mathrm{e} \Gamma$
for the external edge boundary of
$\partial^\mathrm{e} \Gamma$
for the external edge boundary of
![]() $\Gamma$
, i.e. the set of edges
$\Gamma$
, i.e. the set of edges
![]() $e=\langle u,v \rangle$
, with
$e=\langle u,v \rangle$
, with
![]() $u\in \Gamma$
and
$u\in \Gamma$
and
![]() $v\notin \Gamma$
.
$v\notin \Gamma$
.
It is not hard to see that the radius of the open cluster of the CDPRE model decays exponentially fast when
![]() $t<\frac12$
. This follows since the model is stochastically dominated by independent Bernoulli percolation, and the fact that the radius of the open cluster of the latter model decays exponentially fast [Reference Aizenman and Barsky1, Reference Duminil-Copin and Tassion6] below its critical threshold [Reference Kesten12]. Theorem 1, whose proof is deferred to Section 2.2, states that
$t<\frac12$
. This follows since the model is stochastically dominated by independent Bernoulli percolation, and the fact that the radius of the open cluster of the latter model decays exponentially fast [Reference Aizenman and Barsky1, Reference Duminil-Copin and Tassion6] below its critical threshold [Reference Kesten12]. Theorem 1, whose proof is deferred to Section 2.2, states that
![]() $\bar{t}_\mathrm{c}(\rho)$
(and consequently
$\bar{t}_\mathrm{c}(\rho)$
(and consequently
![]() $t_\mathrm{c}(\rho)$
) is strictly larger than
$t_\mathrm{c}(\rho)$
) is strictly larger than
![]() $\frac12$
. It is therefore natural to ask: do we have exponential decay for all t smaller than
$\frac12$
. It is therefore natural to ask: do we have exponential decay for all t smaller than
![]() $t_\mathrm{c}(\rho)$
? We prove exponential decay of the radius of the open cluster for all
$t_\mathrm{c}(\rho)$
? We prove exponential decay of the radius of the open cluster for all
![]() $t<\bar{t}_\mathrm{c}(\rho)$
, giving a partial answer to this question. A nice open problem consists in proving that the model exhibits a sharp phase transition, i.e. that the radius of the open cluster decays exponentially fast for all
$t<\bar{t}_\mathrm{c}(\rho)$
, giving a partial answer to this question. A nice open problem consists in proving that the model exhibits a sharp phase transition, i.e. that the radius of the open cluster decays exponentially fast for all
![]() $t<t_\mathrm{c}(\rho)$
. In particular, this would give
$t<t_\mathrm{c}(\rho)$
. In particular, this would give
![]() $t_\mathrm{c}(\rho)=\bar{t}_\mathrm{c}(\rho)$
.
$t_\mathrm{c}(\rho)=\bar{t}_\mathrm{c}(\rho)$
.
Theorem 1.
![]() $\bar{t}_\mathrm{c}(\rho)>\frac 12$
.
$\bar{t}_\mathrm{c}(\rho)>\frac 12$
.
Let
![]() $\theta_n(t)$
denote the probability that the origin is connected to
$\theta_n(t)$
denote the probability that the origin is connected to
![]() $\partial B(n)$
at time t. We omit
$\partial B(n)$
at time t. We omit
![]() $\rho$
from the notation to keep it clean. We will prove the following theorem.
$\rho$
from the notation to keep it clean. We will prove the following theorem.
Theorem 2. Let
![]() $\rho$
and
$\rho$
and
![]() $t<\bar{t}_\mathrm{c}(\rho)$
be given. There exists
$t<\bar{t}_\mathrm{c}(\rho)$
be given. There exists
![]() $\alpha>0$
such that
$\alpha>0$
such that
![]() $\theta_n(t)\leq {\mathrm{e}}^{-\alpha n}$
for all n.
$\theta_n(t)\leq {\mathrm{e}}^{-\alpha n}$
for all n.
In Section 2, we prove Theorems 1 and 2. The proof of Theorem 1 is obtained by showing a sharp phase transition for an intermediate model. The proof of Theorem 2 consists of an application of a Simon–Lieb-type inequality. In Section 3, we make some final remarks and describe some open problems.
Remark 2. Theorem 2 holds in greater generality under the assumption that the constraint random variables are stationary. Moreover, it remains valid when assuming a model with
![]() $\rho_4>0$
.
$\rho_4>0$
.
2. Proofs
2.1. Proof of Theorem 2
To prove Theorem 2, we will apply a Simon–Lieb-type inequality on boxes of several lengths. Observe that if the origin is connected by an open path to
![]() $\partial B(4n)$
, then the origin must be connected by an open path to
$\partial B(4n)$
, then the origin must be connected by an open path to
![]() $\partial B(n)$
, and there must exist a vertex
$\partial B(n)$
, and there must exist a vertex
![]() $w\in\partial B(2n)$
such that w is connected to
$w\in\partial B(2n)$
such that w is connected to
![]() $\partial B(4n)$
by an open path using edges on the complement of B(2n) only. The main difficulty here is to control the decay of connectivity and the decay of correlations between events whose occurrence depends only on the state of edges inside B(n) and those depending on the state of edges outside B(2n). We observe that the decay of correlations obtained in [Reference Sanchis, dos Santos and Silva15, Theorem 2] is no longer sufficient here, and we derive a new decay rate which is improved by a factor of
$\partial B(4n)$
by an open path using edges on the complement of B(2n) only. The main difficulty here is to control the decay of connectivity and the decay of correlations between events whose occurrence depends only on the state of edges inside B(n) and those depending on the state of edges outside B(2n). We observe that the decay of correlations obtained in [Reference Sanchis, dos Santos and Silva15, Theorem 2] is no longer sufficient here, and we derive a new decay rate which is improved by a factor of
![]() $\log n$
.
$\log n$
.
In what follows, the notation ![]() means that the vertex w is connected to some vertex in B using only edges with both endpoints in A. All constants
means that the vertex w is connected to some vertex in B using only edges with both endpoints in A. All constants
![]() $c_1, c_2, c_3, c_4, c_5$
appearing in this section are universal and do not depend on n, t, or
$c_1, c_2, c_3, c_4, c_5$
appearing in this section are universal and do not depend on n, t, or
![]() $\rho$
.
$\rho$
.
Proposition 1. Fix
![]() $m,n\in\mathbb{N}$
such that
$m,n\in\mathbb{N}$
such that
![]() $2m<n$
and
$2m<n$
and
![]() $w\in \partial B(2m)$
. Then
$w\in \partial B(2m)$
. Then

for all
![]() $\rho=(\rho_0, \rho_1, \rho_2, \rho_3)$
and
$\rho=(\rho_0, \rho_1, \rho_2, \rho_3)$
and
![]() $t\in[0,1]$
.
$t\in[0,1]$
.
Proof. We follow the argument in [Reference Amir and Baldasso3, Section 2.1]. Fix
![]() $t>0$
and let
$t>0$
and let
![]() $M_t(x)$
be the set of vertices y such that there is a path
$M_t(x)$
be the set of vertices y such that there is a path
![]() $x,e_1,x_1,e_2,x_2\dots,e_k,y$
with
$x,e_1,x_1,e_2,x_2\dots,e_k,y$
with
![]() $t>U(e_1)>U(e_2)>\cdots>U(e_k)$
. This gives, with the aid of Stirling’s formula,
$t>U(e_1)>U(e_2)>\cdots>U(e_k)$
. This gives, with the aid of Stirling’s formula,
The first inequality in (1) holds because if
![]() $\{M_t(x)\cap\{x+\partial B(m)\}\neq \emptyset)\}$
occurs, there must exist a self-avoiding path of length m starting at x such that all clocks ring in order before time t.
$\{M_t(x)\cap\{x+\partial B(m)\}\neq \emptyset)\}$
occurs, there must exist a self-avoiding path of length m starting at x such that all clocks ring in order before time t.
Write
![]() $M_t(\partial B(n))=\bigcup_{x\in \partial B(n)}M_t(x)$
and let
$M_t(\partial B(n))=\bigcup_{x\in \partial B(n)}M_t(x)$
and let
![]() $w\in\partial B(2m)$
. The union bound and (1) yields
$w\in\partial B(2m)$
. The union bound and (1) yields
 \begin{align*} \mathbb{P}_{\rho,t}\big(M_t(\partial B(m))\cap M_t(w)\neq \emptyset\big) & \leq 2\mathbb{P}_{\rho,t}\big(M_t(\partial B(m))\cap\partial B(\lfloor3m/2 \rfloor)\neq \emptyset\big) \\[5pt] & \leq c_1m\exp\big({-}\tfrac{1}{2}m\log m\big) \end{align*}
\begin{align*} \mathbb{P}_{\rho,t}\big(M_t(\partial B(m))\cap M_t(w)\neq \emptyset\big) & \leq 2\mathbb{P}_{\rho,t}\big(M_t(\partial B(m))\cap\partial B(\lfloor3m/2 \rfloor)\neq \emptyset\big) \\[5pt] & \leq c_1m\exp\big({-}\tfrac{1}{2}m\log m\big) \end{align*}
for
![]() $m>36{\mathrm{e}}^2$
. Note that on
$m>36{\mathrm{e}}^2$
. Note that on
![]() $\{M_t(\partial B(m))\cap M_t(w)= \emptyset\}$
, the events
$\{M_t(\partial B(m))\cap M_t(w)= \emptyset\}$
, the events ![]() and
and ![]() are determined by random variables on disjoint sets of edges. Hence, in this case the covariance vanishes. Therefore, we obtain
are determined by random variables on disjoint sets of edges. Hence, in this case the covariance vanishes. Therefore, we obtain
The proof follows by observing that

Proof of Theorem
2. Fix
![]() $\rho$
,
$\rho$
,
![]() $t<\bar{t}_\mathrm{c}(\rho)$
, and write
$t<\bar{t}_\mathrm{c}(\rho)$
, and write
![]() $\theta_n(t)\equiv\theta_n$
. Following the discussion at the beginning of this section, let us consider boxes of side length
$\theta_n(t)\equiv\theta_n$
. Following the discussion at the beginning of this section, let us consider boxes of side length
![]() $2\lfloor\sqrt{n}\rfloor$
. We have
$2\lfloor\sqrt{n}\rfloor$
. We have
Applying the union bound and then Proposition 1, we have

By translation invariance we have ![]() for any
for any
![]() $w\in\partial B(2\lfloor\sqrt{n}\rfloor)$
. Hence
$w\in\partial B(2\lfloor\sqrt{n}\rfloor)$
. Hence
Iterating this
![]() $\tfrac12\lfloor\sqrt{n}\rfloor$
times and using the same argument for
$\tfrac12\lfloor\sqrt{n}\rfloor$
times and using the same argument for
![]() $\theta_{n-2j\lfloor\sqrt{n}\rfloor}$
,
$\theta_{n-2j\lfloor\sqrt{n}\rfloor}$
,
![]() $j\in\big\{1,2,\dots,\tfrac12\lfloor\sqrt{n}\rfloor\big\}$
, we obtain
$j\in\big\{1,2,\dots,\tfrac12\lfloor\sqrt{n}\rfloor\big\}$
, we obtain
 \begin{equation} \theta_n \leq \big(c_2\lfloor\sqrt{n}\rfloor\theta_{\lfloor\sqrt{n}\rfloor}\big)^{\tfrac12\lfloor\sqrt{n}\rfloor} + c_1n\exp\big({-}\tfrac12\lfloor\sqrt{n}\rfloor\log\lfloor\sqrt n\rfloor\big) \sum_{i=0}^{\lfloor\sqrt{n}\rfloor-1}\big(c_2\lfloor\sqrt{n}\rfloor\theta_{\lfloor\sqrt{n}\rfloor}\big)^i. \end{equation}
\begin{equation} \theta_n \leq \big(c_2\lfloor\sqrt{n}\rfloor\theta_{\lfloor\sqrt{n}\rfloor}\big)^{\tfrac12\lfloor\sqrt{n}\rfloor} + c_1n\exp\big({-}\tfrac12\lfloor\sqrt{n}\rfloor\log\lfloor\sqrt n\rfloor\big) \sum_{i=0}^{\lfloor\sqrt{n}\rfloor-1}\big(c_2\lfloor\sqrt{n}\rfloor\theta_{\lfloor\sqrt{n}\rfloor}\big)^i. \end{equation}
It is easy to see that if
![]() $\mathbb{E}_{\rho,t}(|C|)<\infty$
then
$\mathbb{E}_{\rho,t}(|C|)<\infty$
then
![]() $\sum_{n\geq 1}\theta_n(t)<\infty$
. Since
$\sum_{n\geq 1}\theta_n(t)<\infty$
. Since
![]() $\{\theta_n(t)\}_n$
is decreasing, an exercise in analysis gives
$\{\theta_n(t)\}_n$
is decreasing, an exercise in analysis gives
Hence we can find some
![]() $n_0\in\mathbb{N}$
such that
$n_0\in\mathbb{N}$
such that
![]() $c_2\lfloor\sqrt{n}\rfloor\theta_{\lfloor\sqrt{n}\rfloor} < {\mathrm{e}}^{-2}$
for all
$c_2\lfloor\sqrt{n}\rfloor\theta_{\lfloor\sqrt{n}\rfloor} < {\mathrm{e}}^{-2}$
for all
![]() $n\geq n_0$
. This gives
$n\geq n_0$
. This gives
for all
![]() $n\geq n_0$
. Note that
$n\geq n_0$
. Note that
 \begin{align*} & c_2n\exp\big({-}\tfrac12\lfloor\sqrt{n}\rfloor\log\lfloor{\sqrt{n}}\rfloor\big)\\[5pt] & = \exp\bigg\{{-}\bigg[\frac{\lfloor\sqrt{n}\rfloor}{2} + \frac{(\log\lfloor{\sqrt{n}}\rfloor-1)\lfloor\sqrt{n}\rfloor}{2} - \log(c_3n)\bigg]\bigg\} \leq \exp\big({-}\tfrac14\sqrt{n}\big) \end{align*}
\begin{align*} & c_2n\exp\big({-}\tfrac12\lfloor\sqrt{n}\rfloor\log\lfloor{\sqrt{n}}\rfloor\big)\\[5pt] & = \exp\bigg\{{-}\bigg[\frac{\lfloor\sqrt{n}\rfloor}{2} + \frac{(\log\lfloor{\sqrt{n}}\rfloor-1)\lfloor\sqrt{n}\rfloor}{2} - \log(c_3n)\bigg]\bigg\} \leq \exp\big({-}\tfrac14\sqrt{n}\big) \end{align*}
for all n large enough, and hence
The same reasoning yields, for any
![]() $n,k\in {\mathbb{N}}$
,
$n,k\in {\mathbb{N}}$
,
![]() $\theta_{2(k+1)n}\leq c_4 n\theta_n\theta_{2kn}+c_4n\exp\big({-}\frac12 n\log n\big)$
. By (4), there exists a large fixed
$\theta_{2(k+1)n}\leq c_4 n\theta_n\theta_{2kn}+c_4n\exp\big({-}\frac12 n\log n\big)$
. By (4), there exists a large fixed
![]() $n=N\in{\mathbb{N}}$
and some constant
$n=N\in{\mathbb{N}}$
and some constant
![]() $c_5$
such that
$c_5$
such that
Here,
![]() $\alpha>1$
can be taken as any fixed number, e.g.
$\alpha>1$
can be taken as any fixed number, e.g.
![]() $\alpha=2$
. We claim that
$\alpha=2$
. We claim that
for all
![]() $k=1,2,\dots,k_{\max}$
. The number
$k=1,2,\dots,k_{\max}$
. The number
![]() $k_{\max}$
will be established below, but it suffices that
$k_{\max}$
will be established below, but it suffices that
![]() $k_{\max}\geq 7$
.
$k_{\max}\geq 7$
.
We prove (5) by induction on k. Since
![]() $\theta_n$
is non-increasing, we have
$\theta_n$
is non-increasing, we have
![]() $\theta_{2N}\leq \theta_N$
, and (5) follows when
$\theta_{2N}\leq \theta_N$
, and (5) follows when
![]() $k=1$
. Let
$k=1$
. Let
Assuming (5) holds for
![]() $k=\ell\in\{1,2,\dots,k_{\max}-1\}$
, the claim follows since
$k=\ell\in\{1,2,\dots,k_{\max}-1\}$
, the claim follows since
In particular, loosening the upper bound
![]() $\theta_{2kN}\leq 1/(2^k\alpha^kc_4N^k)$
, we have that
$\theta_{2kN}\leq 1/(2^k\alpha^kc_4N^k)$
, we have that
-
(i)
 $\theta_m\leq \alpha^{-m/(2N)}$
,
$\theta_m\leq \alpha^{-m/(2N)}$
,
 $m\in\{2N,4N,\dots,2k_{\max}N\}$
;
$m\in\{2N,4N,\dots,2k_{\max}N\}$
; -
(ii)
 $\theta_{N'}\leq {1}/({4\alpha'c_4(N')^2})$
, where
$\theta_{N'}\leq {1}/({4\alpha'c_4(N')^2})$
, where
 $2k_{\max}N=N'$
and
$2k_{\max}N=N'$
and
 $\alpha'=\alpha^{k_{\max}}$
.
$\alpha'=\alpha^{k_{\max}}$
.
Item (ii) follows since if
![]() $k_{\max}\geq 7$
, then
$k_{\max}\geq 7$
, then
![]() $2^{k_{\max}}N^{k_{\max}}\geq 4(2k_{\max}N)^2$
. Repeating the same argument with N’ and
$2^{k_{\max}}N^{k_{\max}}\geq 4(2k_{\max}N)^2$
. Repeating the same argument with N’ and
![]() $\alpha'$
, we obtain a new set of values
$\alpha'$
, we obtain a new set of values
![]() $m\in\{2N',\dots,2k_{\max}N'\}$
, for which
$m\in\{2N',\dots,2k_{\max}N'\}$
, for which
![]() $\theta_m\leq (\alpha')^{-m/(2N')}=\alpha^{-m/(2N)}$
. Continuing inductively, we obtain an infinite subsequence
$\theta_m\leq (\alpha')^{-m/(2N')}=\alpha^{-m/(2N)}$
. Continuing inductively, we obtain an infinite subsequence
![]() $m_1,m_2,\dots$
with the property that
$m_1,m_2,\dots$
with the property that
![]() $m_{j+1}\leq 2m_j$
for all
$m_{j+1}\leq 2m_j$
for all
![]() $j\in{\mathbb{N}}$
, such that
$j\in{\mathbb{N}}$
, such that
![]() $\theta_{m_{j}}\leq \alpha^{-m_j/(2N)}$
. Since
$\theta_{m_{j}}\leq \alpha^{-m_j/(2N)}$
. Since
![]() $\theta_n$
is non-increasing in n, it follows that
$\theta_n$
is non-increasing in n, it follows that
![]() $\theta_n\leq \alpha^{-n/(4N)}$
for all
$\theta_n\leq \alpha^{-n/(4N)}$
for all
![]() $n>N$
. This completes the proof.
$n>N$
. This completes the proof.
2.2. Proof of Theorem 1
In this section we prove Theorem 1. We break the proof into two parts, assuming first that
![]() $0<\rho_0<1$
. Let
$0<\rho_0<1$
. Let
![]() $\{U(e)\}_{e\in\mathcal{E}}$
and
$\{U(e)\}_{e\in\mathcal{E}}$
and
![]() $\{\kappa_v\}_{v\in{\mathbb{Z}}^2}$
be given. Define a new percolation configuration
$\{\kappa_v\}_{v\in{\mathbb{Z}}^2}$
be given. Define a new percolation configuration
![]() $\eta_t$
at edge
$\eta_t$
at edge
![]() $e=\langle u,v \rangle$
as
$e=\langle u,v \rangle$
as
 \begin{equation} \eta_{t,e} = \left\{ \begin{array}{l@{\quad}l} \textbf{1}{\{U(e)\leq t\}} & \text{if}\ v=u+(0,1), \\[5pt] \textbf{1}{\{U(e)\leq t\}}\textbf{1}{\{\kappa_u\neq0\}} \quad & \text{if}\ v=u+(1,0). \end{array} \right.\end{equation}
\begin{equation} \eta_{t,e} = \left\{ \begin{array}{l@{\quad}l} \textbf{1}{\{U(e)\leq t\}} & \text{if}\ v=u+(0,1), \\[5pt] \textbf{1}{\{U(e)\leq t\}}\textbf{1}{\{\kappa_u\neq0\}} \quad & \text{if}\ v=u+(1,0). \end{array} \right.\end{equation}
This corresponds to a percolation model where vertical edges are independently open with probability t and horizontal edges are independently open with probability
![]() $t(1-\rho_0)$
.
$t(1-\rho_0)$
.
Let
![]() $\widehat{\omega}_t$
denote an independent Bernoulli bond percolation configuration with parameter t. According to the terminology used in [Reference Aizenman and Grimmett2, Reference Balister, Bollobás and Riordan4],
$\widehat{\omega}_t$
denote an independent Bernoulli bond percolation configuration with parameter t. According to the terminology used in [Reference Aizenman and Grimmett2, Reference Balister, Bollobás and Riordan4],
![]() $\eta_t$
is an essential diminishment of
$\eta_t$
is an essential diminishment of
![]() $\widehat{\omega}_t$
. This means that there exists a configuration where
$\widehat{\omega}_t$
. This means that there exists a configuration where
![]() $\widehat{\omega}_t(U)$
has a doubly infinite open path, but a doubly infinite open path is not present after the diminishment is activated at the origin. To see this, take a Bernoulli configuration
$\widehat{\omega}_t(U)$
has a doubly infinite open path, but a doubly infinite open path is not present after the diminishment is activated at the origin. To see this, take a Bernoulli configuration
![]() $\widehat{\omega}_t$
and consider the following rule: for each vertex
$\widehat{\omega}_t$
and consider the following rule: for each vertex
![]() $u\in{\mathbb{Z}}^2$
, activate a diminishment at u with probability
$u\in{\mathbb{Z}}^2$
, activate a diminishment at u with probability
![]() $(1-\rho_0)$
. If the diminishment is activated at u, delete the edge
$(1-\rho_0)$
. If the diminishment is activated at u, delete the edge
![]() $v=u+(1,0)$
. This constitutes an essential diminishment (take any configuration where the edge
$v=u+(1,0)$
. This constitutes an essential diminishment (take any configuration where the edge
![]() $\langle (0,0),(1,0)\rangle$
is open, and the events
$\langle (0,0),(1,0)\rangle$
is open, and the events ![]() and
and ![]() occur disjointly), and the diminished configuration follows the same distribution as
occur disjointly), and the diminished configuration follows the same distribution as
![]() $\eta_t$
. Consequently, based on the results in [Reference Aizenman and Grimmett2, Reference Balister, Bollobás and Riordan4], the critical threshold for the model in (6) strictly increases and is therefore larger than
$\eta_t$
. Consequently, based on the results in [Reference Aizenman and Grimmett2, Reference Balister, Bollobás and Riordan4], the critical threshold for the model in (6) strictly increases and is therefore larger than
![]() $\frac12$
. Moreover, due to the stochastic dominance of the random variable
$\frac12$
. Moreover, due to the stochastic dominance of the random variable
![]() $\omega_{t,e}$
by
$\omega_{t,e}$
by
![]() $\eta_{t,e}$
, the desired result can be derived from the sharpness of the phase transition observed for independent inhomogeneous Bernoulli percolation [Reference Aizenman and Barsky1].
$\eta_{t,e}$
, the desired result can be derived from the sharpness of the phase transition observed for independent inhomogeneous Bernoulli percolation [Reference Aizenman and Barsky1].
We turn to the case
![]() $\rho_0=0$
. Based on ideas from [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5], we construct an intermediate model that dominates the CDPRE process when
$\rho_0=0$
. Based on ideas from [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5], we construct an intermediate model that dominates the CDPRE process when
![]() $\rho_0=0$
and is dominated by independent Bernoulli percolation. We will show that the intermediate model phase transition is sharp, yielding the desired result.
$\rho_0=0$
and is dominated by independent Bernoulli percolation. We will show that the intermediate model phase transition is sharp, yielding the desired result.
Let
![]() $\Lambda=[0,5]\times[0,4]$
and
$\Lambda=[0,5]\times[0,4]$
and
![]() $\overline{\Lambda}=[1,4]\times[1,3]$
. For each
$\overline{\Lambda}=[1,4]\times[1,3]$
. For each
![]() $(r,s)\in{\mathbb{Z}}^2$
, define
$(r,s)\in{\mathbb{Z}}^2$
, define
![]() $\Lambda_{r,s}=\Lambda+(6r,5s)$
and
$\Lambda_{r,s}=\Lambda+(6r,5s)$
and
![]() $\overline{\Lambda}_{r,s}=\overline{\Lambda}+(6r,5s)$
. Consider the following sets of edges in
$\overline{\Lambda}_{r,s}=\overline{\Lambda}+(6r,5s)$
. Consider the following sets of edges in
![]() $\mathcal{E}(\Lambda_{r,s})$
:
$\mathcal{E}(\Lambda_{r,s})$
:
 \begin{align*} g_{r,s} & = \langle(6r+2,5s+2),(6r+3,5s+2)\rangle, \\[5pt] A_{r,s} & = \{e\in\mathcal{E}(\overline{\Lambda}_{r,s})\colon|e\cap\partial\overline{\Lambda}_{r,s}|=1\}, \\[5pt] B_{r,s} & = \mathcal{E}(\Lambda_{r,s})\setminus(g_{r,s}\cup A_{r,s}).\end{align*}
\begin{align*} g_{r,s} & = \langle(6r+2,5s+2),(6r+3,5s+2)\rangle, \\[5pt] A_{r,s} & = \{e\in\mathcal{E}(\overline{\Lambda}_{r,s})\colon|e\cap\partial\overline{\Lambda}_{r,s}|=1\}, \\[5pt] B_{r,s} & = \mathcal{E}(\Lambda_{r,s})\setminus(g_{r,s}\cup A_{r,s}).\end{align*}
Observe that
![]() $g_{r,s}$
is not an element of
$g_{r,s}$
is not an element of
![]() $A_{r,s}$
.
$A_{r,s}$
.
The intermediate model is constructed as follows: let
![]() $\{U(e)\}_{e\in\mathcal{E}}$
be an independent collection of uniform random variables on [0,1] with corresponding product measure
$\{U(e)\}_{e\in\mathcal{E}}$
be an independent collection of uniform random variables on [0,1] with corresponding product measure
![]() $\mathbb{P}$
, and define the event
$\mathbb{P}$
, and define the event
See Figure 1 for a sketch of the boxes and edges involved in the construction.

Figure 1.
![]() $\Lambda_{r,s}$
(larger box),
$\Lambda_{r,s}$
(larger box),
![]() $\overline{\Lambda}_{r,s}$
(gray box), and the edge
$\overline{\Lambda}_{r,s}$
(gray box), and the edge
![]() $g_{r,s}$
.
$g_{r,s}$
.
![]() $A_{r,s}$
consists of the dashed edges.
$A_{r,s}$
consists of the dashed edges.
A configuration of the intermediate model is a function
![]() $\widetilde{\omega}_t\colon[0,1]^{\mathcal{E}}\longrightarrow \{0,1\}^{\mathcal{E}}$
such that
$\widetilde{\omega}_t\colon[0,1]^{\mathcal{E}}\longrightarrow \{0,1\}^{\mathcal{E}}$
such that
 \begin{equation} \widetilde{\omega}_{t,e} = \left\{ \begin{array}{l@{\quad}l} \textbf{1}{\{U(e)\leq t\}} & \text{if}\ e\notin\cup_{r,s}\{g_{r,s}\}, \\[5pt] \textbf{1}{\{U(e)\leq t\}}\textbf{1}\{C^\mathrm{c}_{r,s}\} \quad & \text{if}\ e=g_{r,s}. \end{array} \right.\end{equation}
\begin{equation} \widetilde{\omega}_{t,e} = \left\{ \begin{array}{l@{\quad}l} \textbf{1}{\{U(e)\leq t\}} & \text{if}\ e\notin\cup_{r,s}\{g_{r,s}\}, \\[5pt] \textbf{1}{\{U(e)\leq t\}}\textbf{1}\{C^\mathrm{c}_{r,s}\} \quad & \text{if}\ e=g_{r,s}. \end{array} \right.\end{equation}
Note that this has the effect of ‘diminishing’ the percolation configuration by changing the state of some edges from t-open to t-closed. It is important to highlight that there are no constraints in the intermediate model. Write
![]() $\hat{t}_\mathrm{c}$
and
$\hat{t}_\mathrm{c}$
and
![]() $\tilde{t}_\mathrm{c}$
for the susceptibility critical thresholds (the supremum of
$\tilde{t}_\mathrm{c}$
for the susceptibility critical thresholds (the supremum of
![]() $t\in [0,1]$
such that the mean size of the open cluster is finite almost surely) of Bernoulli percolation and the intermediate model, respectively. Note that
$t\in [0,1]$
such that the mean size of the open cluster is finite almost surely) of Bernoulli percolation and the intermediate model, respectively. Note that
![]() $\widetilde{\omega}_{t,e}$
can be obtained through a standard coupling (using the same variables U(e)) with the CDPRE model. In particular, we have
$\widetilde{\omega}_{t,e}$
can be obtained through a standard coupling (using the same variables U(e)) with the CDPRE model. In particular, we have
![]() $\widetilde{\omega}_{t,e}\geq \omega_{t,e}$
for all
$\widetilde{\omega}_{t,e}\geq \omega_{t,e}$
for all
![]() $t\in[0,1]$
and for all
$t\in[0,1]$
and for all
![]() $e\in\mathcal{E}$
, whenever
$e\in\mathcal{E}$
, whenever
![]() $\rho_0=0$
.
$\rho_0=0$
.
Denoting an independent Bernoulli configuration of parameter t by
![]() $\widehat{\omega}_t$
, we observe that
$\widehat{\omega}_t$
, we observe that
![]() $\widetilde{\omega}_t$
is an essential diminishment of
$\widetilde{\omega}_t$
is an essential diminishment of
![]() $\widehat{\omega}_t$
. More precisely, let
$\widehat{\omega}_t$
. More precisely, let
![]() $W=\{x\in\mathbb{Z}^2\colon x=(4r+1,3s+1)$
for some
$W=\{x\in\mathbb{Z}^2\colon x=(4r+1,3s+1)$
for some
![]() $(r,s)\}$
, which consists of vertices that are left end points of some
$(r,s)\}$
, which consists of vertices that are left end points of some
![]() $g_{r,s}$
. Independently activate a diminishment at each vertex
$g_{r,s}$
. Independently activate a diminishment at each vertex
![]() $x\in W$
with probability 1. When activated, the diminishment acts on
$x\in W$
with probability 1. When activated, the diminishment acts on
![]() $\Lambda_{r,s}$
by deleting the edge
$\Lambda_{r,s}$
by deleting the edge
![]() $g_{r,s}$
whenever
$g_{r,s}$
whenever
![]() $C_{r,s}$
occurs. Therefore, applying the main result in [Reference Aizenman and Grimmett2, Reference Balister, Bollobás and Riordan4] once again, we conclude that the critical threshold of the intermediate model is strictly larger than
$C_{r,s}$
occurs. Therefore, applying the main result in [Reference Aizenman and Grimmett2, Reference Balister, Bollobás and Riordan4] once again, we conclude that the critical threshold of the intermediate model is strictly larger than
![]() $\frac12$
.
$\frac12$
.
Assuming that the intermediate model phase transition is sharp, we have the inequality
![]() $\frac12 = \hat{t}_\mathrm{c}< \tilde{t}_\mathrm{c}$
. Since the CDPRE model is dominated by the intermediate model, this gives
$\frac12 = \hat{t}_\mathrm{c}< \tilde{t}_\mathrm{c}$
. Since the CDPRE model is dominated by the intermediate model, this gives
![]() $\frac12 < \tilde{t}_\mathrm{c}\leq \bar{t}_\mathrm{c}(\rho)$
for all
$\frac12 < \tilde{t}_\mathrm{c}\leq \bar{t}_\mathrm{c}(\rho)$
for all
![]() $\rho$
with
$\rho$
with
![]() $\rho_0=0$
.
$\rho_0=0$
.
Remark 3. We observe that the domination argument described above does not hold when
![]() $\rho_0>0$
. For instance, suppose
$\rho_0>0$
. For instance, suppose
![]() $\kappa_{(2,3)}=\kappa_{(3,3)}=0$
and
$\kappa_{(2,3)}=\kappa_{(3,3)}=0$
and
![]() $\kappa_{(2,2)}=\kappa_{(3,2)}=3$
. If
$\kappa_{(2,2)}=\kappa_{(3,2)}=3$
. If
![]() $C_{0,0}$
occurs, then
$C_{0,0}$
occurs, then
![]() $\widetilde{\omega}_{t,g_{0,0}}=0$
while
$\widetilde{\omega}_{t,g_{0,0}}=0$
while
![]() ${\omega}_{t,g_{0,0}}=1$
.
${\omega}_{t,g_{0,0}}=1$
.
Based on the ideas developed in [Reference Duminil-Copin, Raoufi and Tassion7], we will prove the sharpness of the phase transition for the intermediate model by applying the O’Donnell–Saks–Schramm–Servedio (OSSS) inequality for Boolean functions and a suitable randomized algorithm.
Let us introduce some further notation. Assume I is a countable set, and let
![]() $(\Omega^I,\pi^{\otimes I})$
be a product probability space with elements denoted by
$(\Omega^I,\pi^{\otimes I})$
be a product probability space with elements denoted by
![]() $\omega=(\omega_i)_{i\in I}$
. Consider a Boolean function
$\omega=(\omega_i)_{i\in I}$
. Consider a Boolean function
![]() $f\colon\Omega^I\rightarrow\{0,1\}$
. An algorithm
$f\colon\Omega^I\rightarrow\{0,1\}$
. An algorithm
![]() $\textbf{T}$
determining f takes a configuration
$\textbf{T}$
determining f takes a configuration
![]() $\omega$
as input and reveals the value of
$\omega$
as input and reveals the value of
![]() $\omega$
in different coordinates one by one. At each step, the next coordinate to be revealed depends on the values of
$\omega$
in different coordinates one by one. At each step, the next coordinate to be revealed depends on the values of
![]() $\omega$
revealed so far. This process continues until the value of f is determined, regardless of the values of
$\omega$
revealed so far. This process continues until the value of f is determined, regardless of the values of
![]() $\omega$
on the remaining coordinates. We refer the reader to [Reference O’Donnell, Saks, Schramm and Servedio14] for a formal description of a randomized algorithm.
$\omega$
on the remaining coordinates. We refer the reader to [Reference O’Donnell, Saks, Schramm and Servedio14] for a formal description of a randomized algorithm.
Denote by
![]() $\delta_i(\textbf{T})$
and
$\delta_i(\textbf{T})$
and
![]() $\mathrm{Inf}_i(f)$
the revealment and the influence of the ith coordinate, respectively, defined as follows:
$\mathrm{Inf}_i(f)$
the revealment and the influence of the ith coordinate, respectively, defined as follows:
 \begin{align*} \delta_i(\textbf{T}) & := \pi^{\otimes I}(\textbf{T}\mbox{ reveals the value of $\omega_i$}), \\[5pt] \mathrm{Inf}_i(f) & := \pi^{\otimes I}(f(\omega)\neq f(\omega^*)),\end{align*}
\begin{align*} \delta_i(\textbf{T}) & := \pi^{\otimes I}(\textbf{T}\mbox{ reveals the value of $\omega_i$}), \\[5pt] \mathrm{Inf}_i(f) & := \pi^{\otimes I}(f(\omega)\neq f(\omega^*)),\end{align*}
where
![]() $\omega^*$
is equal to
$\omega^*$
is equal to
![]() $\omega$
in every coordinate except the ith coordinate, which is resampled independently. The OSSS inequality [Reference O’Donnell, Saks, Schramm and Servedio14] provides a bound on the variance of f in terms of the influence and the computational complexity of an algorithm for this function. It states that for any function
$\omega$
in every coordinate except the ith coordinate, which is resampled independently. The OSSS inequality [Reference O’Donnell, Saks, Schramm and Servedio14] provides a bound on the variance of f in terms of the influence and the computational complexity of an algorithm for this function. It states that for any function
![]() $f\colon\Omega^I\rightarrow\{0,1\}$
and any algorithm
$f\colon\Omega^I\rightarrow\{0,1\}$
and any algorithm
![]() $\textbf{T}$
determining f,
$\textbf{T}$
determining f,
Since the state of any edge
![]() $g_{r,s}$
depends only on U(e) for
$g_{r,s}$
depends only on U(e) for
![]() $e\in\Lambda_{r,s}$
, the intermediate model is a 3-dependent percolation process and the OSSS inequality cannot be directly applied. To overcome this difficulty, we introduce a suitable product space to encode the measure of the intermediate model. We take
$e\in\Lambda_{r,s}$
, the intermediate model is a 3-dependent percolation process and the OSSS inequality cannot be directly applied. To overcome this difficulty, we introduce a suitable product space to encode the measure of the intermediate model. We take
![]() $\Omega=[0,1]$
,
$\Omega=[0,1]$
,
![]() $I=\mathcal{E}$
, and
$I=\mathcal{E}$
, and
![]() $\pi^{\otimes I}=\mathbb{P}$
. Writing
$\pi^{\otimes I}=\mathbb{P}$
. Writing ![]() , we are interested in bounding the variance of the Boolean function
, we are interested in bounding the variance of the Boolean function
![]() $\textbf{1}\{\widetilde{\omega}_t^{-1}(\mathcal{B}_n)\}$
considered as a function from
$\textbf{1}\{\widetilde{\omega}_t^{-1}(\mathcal{B}_n)\}$
considered as a function from
![]() $[0,1]^{\mathcal{E}}$
onto
$[0,1]^{\mathcal{E}}$
onto
![]() $\{0,1\}$
.
$\{0,1\}$
.
2.2.1. Bound on the revealment
Recall the definition of
![]() $\widetilde{\omega}_t$
in (7) and denote by
$\widetilde{\omega}_t$
in (7) and denote by
![]() $\widetilde{P}_t$
the law of the intermediate model, i.e.
$\widetilde{P}_t$
the law of the intermediate model, i.e.
![]() $\widetilde{P}_t(A)=\mathbb{P}(U\in[0,1]^{\mathcal{E}}\colon\widetilde{\omega}_t(U)\in{A})$
for all
$\widetilde{P}_t(A)=\mathbb{P}(U\in[0,1]^{\mathcal{E}}\colon\widetilde{\omega}_t(U)\in{A})$
for all
![]() ${A}\subset\{0,1\}^{\mathcal{E}}$
. Write
${A}\subset\{0,1\}^{\mathcal{E}}$
. Write
![]() $\widetilde{\theta}_n(t)=\widetilde{P}_t(\mathcal{B}_n)$
and
$\widetilde{\theta}_n(t)=\widetilde{P}_t(\mathcal{B}_n)$
and
![]() $S_n(t)=\sum_{k=1}^n\widetilde{\theta}_k(t)$
. The next lemma shows the existence of an algorithm determining the Boolean function
$S_n(t)=\sum_{k=1}^n\widetilde{\theta}_k(t)$
. The next lemma shows the existence of an algorithm determining the Boolean function
![]() $\textbf{1}\{\widetilde{\omega}_t^{-1}(\mathcal{B}_n)\}$
and gives an upper bound on its revealment. For each
$\textbf{1}\{\widetilde{\omega}_t^{-1}(\mathcal{B}_n)\}$
and gives an upper bound on its revealment. For each
![]() $(r,s)\in{\mathbb{Z}}^2$
, write
$(r,s)\in{\mathbb{Z}}^2$
, write
![]() $g_{r,s}=\langle u_{r,s},v_{r,s}\rangle$
.
$g_{r,s}=\langle u_{r,s},v_{r,s}\rangle$
.
Lemma 1. For any
![]() $k\in\{0,\dots,n\}$
, there exists an algorithm
$k\in\{0,\dots,n\}$
, there exists an algorithm
![]() $\textbf{T}_k$
determining
$\textbf{T}_k$
determining
![]() $\textbf{1}\{\widetilde{\omega}_t^{-1}(\mathcal{B}_n)\}$
with the property that, for each
$\textbf{1}\{\widetilde{\omega}_t^{-1}(\mathcal{B}_n)\}$
with the property that, for each
![]() $e=\langle x_1,x_2\rangle\in\mathcal{E}$
,
$e=\langle x_1,x_2\rangle\in\mathcal{E}$
,
Once Lemma 1 is proved, observe that, for any
![]() $x\in B(n)$
, by summing (9) over k, we get
$x\in B(n)$
, by summing (9) over k, we get
where the last inequality follows by translation invariance. Plugging (10) into (9) yields
for some constant
![]() $\beta>0$
.
$\beta>0$
.
Let
![]() $F_n$
denote the set of edges between two vertices within a distance n of the origin. We define our algorithm using two growing sequences,
$F_n$
denote the set of edges between two vertices within a distance n of the origin. We define our algorithm using two growing sequences,
![]() $\partial B(k)=Z_0\subset Z_1\subset\dots\subset {\mathbb{Z}}^2$
and
$\partial B(k)=Z_0\subset Z_1\subset\dots\subset {\mathbb{Z}}^2$
and
![]() $\emptyset=F_0\subset F_1\subset\dots\subset F_n$
. At step m, we see
$\emptyset=F_0\subset F_1\subset\dots\subset F_n$
. At step m, we see
![]() $Z_m$
as representing the set of vertices that the algorithm found to be connected to
$Z_m$
as representing the set of vertices that the algorithm found to be connected to
![]() $\partial B(k)$
, and
$\partial B(k)$
, and
![]() $F_m$
as the set of edges explored by the algorithm.
$F_m$
as the set of edges explored by the algorithm.
Definition 1. (Algorithm
![]() $\textbf{T}_k$
.) Algorithm
$\textbf{T}_k$
.) Algorithm
![]() $\textbf{T}_k$
is defined as follows. Let
$\textbf{T}_k$
is defined as follows. Let
![]() $e_1, e_2, \dots$
be a fixed ordering of the edges in
$e_1, e_2, \dots$
be a fixed ordering of the edges in
![]() $E_n$
. Write
$E_n$
. Write
![]() $F_0=\emptyset$
and
$F_0=\emptyset$
and
![]() $Z_0=\partial B(k)$
. Assume
$Z_0=\partial B(k)$
. Assume
![]() $Z_m\subset {\mathbb{Z}}^2$
and
$Z_m\subset {\mathbb{Z}}^2$
and
![]() $F_m\subset E_n$
are given.
$F_m\subset E_n$
are given.
-
(i) If there is an edge
 $e=\langle x,y \rangle\in E_n\setminus F_m$
with
$e=\langle x,y \rangle\in E_n\setminus F_m$
with
 $x\in Z_m$
and
$x\in Z_m$
and
 $y\notin Z_m$
, choose the earliest one according to the fixed ordering, set
$y\notin Z_m$
, choose the earliest one according to the fixed ordering, set
 $F_{m+1}=F_m\cup\{e\}$
, and write
$F_{m+1}=F_m\cup\{e\}$
, and write  \begin{equation*} Z_{m+1} = \left\{ \begin{array}{l@{\quad}l} Z_m\cup\{y\} \quad & \text{if}\ \omega_{t,e}=1, \\[5pt] Z_m & \text{otherwise}. \end{array} \right. \end{equation*}
\begin{equation*} Z_{m+1} = \left\{ \begin{array}{l@{\quad}l} Z_m\cup\{y\} \quad & \text{if}\ \omega_{t,e}=1, \\[5pt] Z_m & \text{otherwise}. \end{array} \right. \end{equation*}
-
(ii) If such an e does not exist, write
 $Z_{m+1}=Z_m$
and
$Z_{m+1}=Z_m$
and
 $F_{m+1}=F_m\cup\{e\}$
.
$F_{m+1}=F_m\cup\{e\}$
.
Note that, as long as we are in the first case of Definition 1, we are still discovering the connected component of
![]() $\partial B(k)$
. On the other hand, as soon as we are in the second case, we remain there. Also, observe that the event where the origin is connected to the boundary of B(n) is already determined before we leave the first case. We are ready to prove Lemma 1.
$\partial B(k)$
. On the other hand, as soon as we are in the second case, we remain there. Also, observe that the event where the origin is connected to the boundary of B(n) is already determined before we leave the first case. We are ready to prove Lemma 1.
Proof of Lemma
1. First, note that the algorithm
![]() $\textbf{T}_k$
discovers the union of all open components of
$\textbf{T}_k$
discovers the union of all open components of
![]() $\partial B(k)$
at time t; in particular, it determines the function
$\partial B(k)$
at time t; in particular, it determines the function
![]() $\textbf{1}\{\widetilde{\omega}_t^{-1}(\mathcal{B}_n)\}$
. Observe that
$\textbf{1}\{\widetilde{\omega}_t^{-1}(\mathcal{B}_n)\}$
. Observe that
![]() $e=\langle x,y \rangle\in\Lambda_{r,s}$
is revealed if and only if either x, y,
$e=\langle x,y \rangle\in\Lambda_{r,s}$
is revealed if and only if either x, y,
![]() $u_{r,s}$
, or
$u_{r,s}$
, or
![]() $v_{r,s}$
are connected by a t-open path to
$v_{r,s}$
are connected by a t-open path to
![]() $\partial B(k)$
. Indeed, to determine the status of
$\partial B(k)$
. Indeed, to determine the status of
![]() $g_{r,s}$
, all edges in
$g_{r,s}$
, all edges in
![]() $\Lambda_{r,s}$
must be revealed. If
$\Lambda_{r,s}$
must be revealed. If
![]() $e\notin \Lambda_{r,s}$
for all (r,s), then e is revealed if and only if x or y are connected to
$e\notin \Lambda_{r,s}$
for all (r,s), then e is revealed if and only if x or y are connected to
![]() $\partial B(k)$
. This completes the proof.
$\partial B(k)$
. This completes the proof.
2.2.2. A Russo-type formula
As before, let
![]() $\mathcal{B}_n$
be the event that the origin is connected to the boundary of the box B(n). We have the following Russo-type formula.
$\mathcal{B}_n$
be the event that the origin is connected to the boundary of the box B(n). We have the following Russo-type formula.
Lemma 2. Let
![]() $0<\alpha_1<\alpha_2<1$
. There exists a constant
$0<\alpha_1<\alpha_2<1$
. There exists a constant
![]() $q>0$
such that, for all
$q>0$
such that, for all
![]() $t\in[\alpha_1,\alpha_2]$
,
$t\in[\alpha_1,\alpha_2]$
,
Proof. Let
![]() $\delta>0$
. Then
$\delta>0$
. Then
 \begin{align} & \widetilde{P}_{t+\delta}(\mathcal{B}_n) - \widetilde{P}_t(\mathcal{B}_n) \nonumber \\[5pt] & \quad = \mathbb{P}(\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n) \nonumber \\[5pt] & \quad = \mathbb{P}\big(\widetilde{\omega}_{t+\delta}\in \mathcal{B}_n,\ \widetilde{\omega}_t\notin \mathcal{B}_n,\ \text{there exists}\ e\in\mathcal{E}(B_n)\ \text{such that}\ t<U(e)\leq t+\delta\big). \end{align}
\begin{align} & \widetilde{P}_{t+\delta}(\mathcal{B}_n) - \widetilde{P}_t(\mathcal{B}_n) \nonumber \\[5pt] & \quad = \mathbb{P}(\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n) \nonumber \\[5pt] & \quad = \mathbb{P}\big(\widetilde{\omega}_{t+\delta}\in \mathcal{B}_n,\ \widetilde{\omega}_t\notin \mathcal{B}_n,\ \text{there exists}\ e\in\mathcal{E}(B_n)\ \text{such that}\ t<U(e)\leq t+\delta\big). \end{align}
Let
![]() $W_{t,\delta}$
be the random set of edges f such that
$W_{t,\delta}$
be the random set of edges f such that
![]() $t<U(f)\leq t+\delta$
. Clearly,
$t<U(f)\leq t+\delta$
. Clearly,
![]() $\mathbb{P}(|W_{t,\delta}|\geq 2)=o(\delta)$
. From this and (12), we obtain
$\mathbb{P}(|W_{t,\delta}|\geq 2)=o(\delta)$
. From this and (12), we obtain
 \begin{align*} \widetilde{P}_{t+\delta}(\mathcal{B}_n) - \widetilde{P}_t(\mathcal{B}_n) & = \mathbb{P}\big(\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n,\ |W_{t,\delta}|=1\big) + o(\delta) \nonumber \\[5pt] & = \sum_{e\in\mathcal{E}(B(n))}\mathbb{P}\big(\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n,\ W_{t,\delta}=\{e\}\big) + o(\delta). \end{align*}
\begin{align*} \widetilde{P}_{t+\delta}(\mathcal{B}_n) - \widetilde{P}_t(\mathcal{B}_n) & = \mathbb{P}\big(\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n,\ |W_{t,\delta}|=1\big) + o(\delta) \nonumber \\[5pt] & = \sum_{e\in\mathcal{E}(B(n))}\mathbb{P}\big(\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n,\ W_{t,\delta}=\{e\}\big) + o(\delta). \end{align*}
We now consider three cases. Remember that
![]() $\mathcal{E}(\Lambda_{r,s})=\{g_{r,s}\}\cup A_{r,s}\cup B_{r,s}$
. First, let
$\mathcal{E}(\Lambda_{r,s})=\{g_{r,s}\}\cup A_{r,s}\cup B_{r,s}$
. First, let
![]() $e\in\mathcal{E}(B(n))-\bigcup_{r,s}\mathcal{E}(\Lambda_{r,s})$
. Then
$e\in\mathcal{E}(B(n))-\bigcup_{r,s}\mathcal{E}(\Lambda_{r,s})$
. Then
 \begin{align*} \mathbb{P}\big(\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n,\ W_{t,\delta}=\{e\}\big) & = \mathbb{P}\big(e\ \text{is pivotal for}\ \mathcal{B}_n\ \text{in}\ \widetilde{\omega}_t,\ W_{t,\delta}=\{e\}\big) + o(\delta) \\[5pt] & = \delta\times\mathbb{P}(e\ \text{is pivotal for}\ \mathcal{B}_n\ \text{in}\ \widetilde{\omega}_t) + o(\delta) \\[5pt] & = \delta\times\widetilde{P}_t(e\ \text{is pivotal for}\ \mathcal{B}_n) + o(\delta). \end{align*}
\begin{align*} \mathbb{P}\big(\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n,\ W_{t,\delta}=\{e\}\big) & = \mathbb{P}\big(e\ \text{is pivotal for}\ \mathcal{B}_n\ \text{in}\ \widetilde{\omega}_t,\ W_{t,\delta}=\{e\}\big) + o(\delta) \\[5pt] & = \delta\times\mathbb{P}(e\ \text{is pivotal for}\ \mathcal{B}_n\ \text{in}\ \widetilde{\omega}_t) + o(\delta) \\[5pt] & = \delta\times\widetilde{P}_t(e\ \text{is pivotal for}\ \mathcal{B}_n) + o(\delta). \end{align*}
Now let
![]() $e=g_{r,s}=\langle u_{r,s},v_{r,s}\rangle$
for some pair (r,s). Consider the event
$e=g_{r,s}=\langle u_{r,s},v_{r,s}\rangle$
for some pair (r,s). Consider the event
Observing that
![]() $\{X, W_{t,\delta}=\{e\}\}\subset C^\mathrm{c}_{r,s}$
, we obtain the inclusion
$\{X, W_{t,\delta}=\{e\}\}\subset C^\mathrm{c}_{r,s}$
, we obtain the inclusion
Note that the event
![]() $X\cap\{e\ \text{is pivotal for}\ \mathcal{B}_n\ \text{in}\ \widetilde{\omega}_t\}$
depends only on the variables U(f) with
$X\cap\{e\ \text{is pivotal for}\ \mathcal{B}_n\ \text{in}\ \widetilde{\omega}_t\}$
depends only on the variables U(f) with
![]() $f\neq g_{r,s}$
. Hence
$f\neq g_{r,s}$
. Hence
Since
![]() $\mathbb{P}(X \mid e \mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t)>0$
for all
$\mathbb{P}(X \mid e \mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t)>0$
for all
![]() $t\in[\alpha_1,\alpha_2]$
, and since the function
$t\in[\alpha_1,\alpha_2]$
, and since the function
![]() $t\rightarrow \mathbb{P}(\widetilde{\omega}_t \in A)$
is continuous for any local event A, Weierstrass’s theorem implies the existence of a constant
$t\rightarrow \mathbb{P}(\widetilde{\omega}_t \in A)$
is continuous for any local event A, Weierstrass’s theorem implies the existence of a constant
![]() $M_1>0$
such that
$M_1>0$
such that
Finally, let
![]() $e\in A_{r,s}\cup B_{r,s}$
and write
$e\in A_{r,s}\cup B_{r,s}$
and write
![]() $Y=\{U(g_{r,s})<U(f)\}$
, where
$Y=\{U(g_{r,s})<U(f)\}$
, where
![]() $f\in A_{r,s}\cup B_{r,s}$
,
$f\in A_{r,s}\cup B_{r,s}$
,
![]() $f\neq e$
. Observe that
$f\neq e$
. Observe that
 \begin{align*} \big\{\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n,\ W_{t,\delta}=\{e\}\big\} & = \big\{e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t,\ W_{t,\delta}=\{e\}\big\} \\[5pt] & \supset \big\{Y,\ e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t,\ W_{t,\delta}=\{e\}\big\}. \end{align*}
\begin{align*} \big\{\widetilde{\omega}_{t+\delta}\in\mathcal{B}_n,\ \widetilde{\omega}_t\notin\mathcal{B}_n,\ W_{t,\delta}=\{e\}\big\} & = \big\{e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t,\ W_{t,\delta}=\{e\}\big\} \\[5pt] & \supset \big\{Y,\ e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t,\ W_{t,\delta}=\{e\}\big\}. \end{align*}
Note that the event
![]() $Y\cap\{e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t\}$
depends only on the variables U(f) with
$Y\cap\{e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t\}$
depends only on the variables U(f) with
![]() $f\neq e$
. Therefore, as in the previous case, there exists a constant
$f\neq e$
. Therefore, as in the previous case, there exists a constant
![]() $M_2>0$
such that
$M_2>0$
such that
 \begin{align*} \mathbb{P}\big(Y,\ e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t,W_{t,\delta}=\{e\}\big) & = \mathbb{P}\big(Y,\ e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t\big) \mathbb{P}(W_{t,\delta}=\{e\}) \\[5pt] & \geq M_2\delta\times\widetilde{P}_t(e \mbox{ is pivotal for }\mathcal{B}_n). \end{align*}
\begin{align*} \mathbb{P}\big(Y,\ e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t,W_{t,\delta}=\{e\}\big) & = \mathbb{P}\big(Y,\ e\mbox{ is pivotal for }\mathcal{B}_n\mbox{ in }\widetilde{\omega}_t\big) \mathbb{P}(W_{t,\delta}=\{e\}) \\[5pt] & \geq M_2\delta\times\widetilde{P}_t(e \mbox{ is pivotal for }\mathcal{B}_n). \end{align*}
Taking
![]() $q=\min\{M_1,M_2\}$
, we obtain
$q=\min\{M_1,M_2\}$
, we obtain
The result follows by dividing both sides by
![]() $\delta$
and taking the limit when
$\delta$
and taking the limit when
![]() $\delta$
goes to zero.
$\delta$
goes to zero.
2.2.3. A bound on the influences
We now seek a bound on the influence of an edge
![]() $e\in \mathcal{E}(B(n))$
on
$e\in \mathcal{E}(B(n))$
on
![]() $\textbf{1}\{\mathcal{B}_n\}$
, i.e. we seek a bound on
$\textbf{1}\{\mathcal{B}_n\}$
, i.e. we seek a bound on
![]() $\mathrm{Inf}_e(\textbf{1}\{\mathcal{B}_n\}):=\mathbb{P}\big(U\colon\textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U))\neq\textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U^*))\big)$
, where U is equal to
$\mathrm{Inf}_e(\textbf{1}\{\mathcal{B}_n\}):=\mathbb{P}\big(U\colon\textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U))\neq\textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U^*))\big)$
, where U is equal to
![]() $U^*$
for every edge except edge e, which is resampled independently. We do this in two steps. First, assume
$U^*$
for every edge except edge e, which is resampled independently. We do this in two steps. First, assume
![]() $e\in\big(\bigcup_{r,s}\mathcal{E}(\Lambda_{r,s})\big)^\mathrm{c}\cup \{g_{r,s}\}$
for some pair (r,s). In this case, the probability that the state of the indicator function changes is
$e\in\big(\bigcup_{r,s}\mathcal{E}(\Lambda_{r,s})\big)^\mathrm{c}\cup \{g_{r,s}\}$
for some pair (r,s). In this case, the probability that the state of the indicator function changes is
for some constant
![]() $\lambda>0$
.
$\lambda>0$
.
Next, let
![]() $e\in \mathcal{E}(\Lambda_{r,s})\setminus \{g_{r,s}\}$
. We have
$e\in \mathcal{E}(\Lambda_{r,s})\setminus \{g_{r,s}\}$
. We have
 \begin{align*} \mathrm{Inf}_e(\textbf{1}\{\mathcal{B}_n\}) & \leq \mathbb{P}\big(U\colon\textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U)) \neq \textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U^*)), U(g_{r,s})>t\big) \\[5pt] & \quad + \mathbb{P}\big(U\colon\textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U)) \neq \textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U^*)), U(g_{r,s})\leq t\big).\end{align*}
\begin{align*} \mathrm{Inf}_e(\textbf{1}\{\mathcal{B}_n\}) & \leq \mathbb{P}\big(U\colon\textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U)) \neq \textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U^*)), U(g_{r,s})>t\big) \\[5pt] & \quad + \mathbb{P}\big(U\colon\textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U)) \neq \textbf{1}\{\mathcal{B}_n\}(\widetilde{\omega}_t(U^*)), U(g_{r,s})\leq t\big).\end{align*}
If
![]() $U(g_{r,s})>t$
and the indicator of
$U(g_{r,s})>t$
and the indicator of
![]() $\mathcal{B}_n$
is changed, then e must be pivotal for
$\mathcal{B}_n$
is changed, then e must be pivotal for
![]() $\mathcal{B}_n$
. If
$\mathcal{B}_n$
. If
![]() $U(g_{r,s})\leq t$
and the indicator of
$U(g_{r,s})\leq t$
and the indicator of
![]() $\mathcal{B}_n$
is changed, then either e or
$\mathcal{B}_n$
is changed, then either e or
![]() $g_{r,s}$
must be pivotal for
$g_{r,s}$
must be pivotal for
![]() $\mathcal{B}_n$
. Putting all this together, we obtain
$\mathcal{B}_n$
. Putting all this together, we obtain
for some constant
![]() $\gamma>0$
.
$\gamma>0$
.
Let
![]() $t_\mathrm{c}^*$
denote the percolation critical threshold for the intermediate model. By stochastic dominance and the results of [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5], we know that
$t_\mathrm{c}^*$
denote the percolation critical threshold for the intermediate model. By stochastic dominance and the results of [Reference de Lima, Sanchis, dos Santos, Sidoravicius and Teodoro5], we know that
![]() $\frac12 <t_\mathrm{c}^*<1$
. We now prove that the intermediate model undergoes a sharp phase transition, a fact of which Theorem 1 is a corollary.
$\frac12 <t_\mathrm{c}^*<1$
. We now prove that the intermediate model undergoes a sharp phase transition, a fact of which Theorem 1 is a corollary.
Theorem 3. Consider the intermediate model on
![]() ${\mathbb{Z}}^2$
.
${\mathbb{Z}}^2$
.
-
(i) For
 $t<t_\mathrm{c}^*$
, there exists
$t<t_\mathrm{c}^*$
, there exists
 $c_t>0$
such that, for all
$c_t>0$
such that, for all
 $n\geq 1$
,
$n\geq 1$
,
 $\widetilde{\theta}_n(t)\leq \exp(-c_tn)$
.
$\widetilde{\theta}_n(t)\leq \exp(-c_tn)$
. -
(ii) There exists
 $c>0$
such that, for
$c>0$
such that, for
 $t>t_\mathrm{c}^*$
,
$t>t_\mathrm{c}^*$
,  .
.
Proof. Applying the OSSS inequality (8) for each k and then summing on k, (11) gives
The inequality in (13) and Lemma 2 give
Hence, there is a constant
![]() $\nu>0$
such that
$\nu>0$
such that
Fix
![]() $t_0\in(t_\mathrm{c}^*,\alpha_2)$
. Since
$t_0\in(t_\mathrm{c}^*,\alpha_2)$
. Since
![]() $\widetilde{\theta}_n(t)$
is increasing in t and n, we have
$\widetilde{\theta}_n(t)$
is increasing in t and n, we have
![]() $1-\widetilde{\theta}_n(t)\geq 1-\widetilde{\theta}_1(t_0)$
for all
$1-\widetilde{\theta}_n(t)\geq 1-\widetilde{\theta}_1(t_0)$
for all
![]() $t\leq t_0$
. The result follows with an application of [Reference Duminil-Copin, Raoufi and Tassion7, Lemma 3] to the function
$t\leq t_0$
. The result follows with an application of [Reference Duminil-Copin, Raoufi and Tassion7, Lemma 3] to the function
3. Final remarks
We conclude this paper with a few remarks and some unanswered questions.
-
(i) Does
 $t_\mathrm{c}(\rho)=\bar{t}_\mathrm{c}(\rho)$
hold for any
$t_\mathrm{c}(\rho)=\bar{t}_\mathrm{c}(\rho)$
hold for any
 $\rho=(\rho_0,\rho_1,\rho_2,\rho_3)$
? One approach to tackle this problem is to demonstrate a sharp phase transition for the CDPRE model, meaning that the radius of the open cluster decays exponentially fast for all
$\rho=(\rho_0,\rho_1,\rho_2,\rho_3)$
? One approach to tackle this problem is to demonstrate a sharp phase transition for the CDPRE model, meaning that the radius of the open cluster decays exponentially fast for all
 $t<t_\mathrm{c}(\rho)$
. The OSSS method in [Reference Duminil-Copin, Raoufi and Tassion7], for example, emerges as a promising tool to prove such decay. On one hand, there is a small and well-controlled probability that we need to look at a distant edge to determine the state of a fixed edge f (because the sequence of the U(e) needs to be decreasing; see also Proposition 1). Hence, when exploring, it should not be difficult to explore the cluster along with the additional edges needed to determine f. On the other hand, proving a Margulis–Russo-type formula seems problematic, given that events of interest are not even monotone in the uniform variables and that the 0–1 variables do not vary nicely in terms of the parameter.
$t<t_\mathrm{c}(\rho)$
. The OSSS method in [Reference Duminil-Copin, Raoufi and Tassion7], for example, emerges as a promising tool to prove such decay. On one hand, there is a small and well-controlled probability that we need to look at a distant edge to determine the state of a fixed edge f (because the sequence of the U(e) needs to be decreasing; see also Proposition 1). Hence, when exploring, it should not be difficult to explore the cluster along with the additional edges needed to determine f. On the other hand, proving a Margulis–Russo-type formula seems problematic, given that events of interest are not even monotone in the uniform variables and that the 0–1 variables do not vary nicely in terms of the parameter. -
(ii) Does the statement of Theorem 2 hold for
 $d>2$
? If we take
$d>2$
? If we take
 $d>2$
, then there would be an entropy factor of order
$d>2$
, then there would be an entropy factor of order
 $n^{d-1}$
in the first term on the right-hand side of (2). In this case we would not have (3), which is crucial for our estimate.
$n^{d-1}$
in the first term on the right-hand side of (2). In this case we would not have (3), which is crucial for our estimate. -
(iii) Assume
 $\rho$
stochastically dominates
$\rho$
stochastically dominates
 $\tilde{\rho}$
. Does
$\tilde{\rho}$
. Does
 $t_\mathrm{c}(\rho)\leq t_\mathrm{c}(\tilde{\rho})$
hold?
$t_\mathrm{c}(\rho)\leq t_\mathrm{c}(\tilde{\rho})$
hold?
Acknowledgements
We are grateful to Rémy Sanchis for several valuable discussions. Diogo C. dos Santos was partially supported by PNPD/CAPES. Roger Silva was partially supported by Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG), grants APQ-00774-21 and APQ-00868-21.
Funding information
There are no funding bodies to thank relating to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.