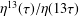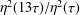1 results
EISENSTEIN SERIES TO THE TREDECIC BASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 June 2014, pp. 19-28
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
-
We employ a modular method to establish the new result that two types of Eisenstein series to the tredecic base may be parametrised in terms of the eta quotients
${\it\eta}^{13}({\it\tau})/{\it\eta}(13{\it\tau})$ and 
${\it\eta}^{2}(13{\it\tau})/{\it\eta}^{2}({\it\tau})$. The method can also be used to give short and simple proofs for the analogous cubic, quintic and septic theories.
