1 results
Multiple buying or selling with vector offers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 959-973
- Print publication:
- December 1997
-
- Article
- Export citation
-
We consider a generalization of the house-selling problem to selling k houses. Let the offers, X1, X2, · ··, be independent, identically distributed k-dimensional random vectors having a known distribution with finite second moments. The decision maker is to choose simultaneously k stopping rules, N1, · ··, Nk, one for each component. The payoff is the sum over j of the jth component of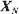
minus a constant cost per observation until all stopping rules have stopped. Simple descriptions of the optimal rules are found. Extension is made to problems with recall of past offers and to problems with a discount.
minus a constant cost per observation until all stopping rules have stopped. Simple descriptions of the optimal rules are found. Extension is made to problems with recall of past offers and to problems with a discount.