Bishop’s presentation of his informal system of constructive mathematics BISH was on purpose closer to the proof-irrelevance of classical mathematics, although a form of proof-relevance was evident in the use of several notions of moduli (of convergence, of uniform continuity, of uniform differentiability, etc.). Focusing on membership and equality conditions for sets given by appropriate existential formulas, we define certain families of proof sets that provide a BHK-interpretation of formulas that correspond to the standard atomic formulas of a first-order theory, within Bishop set theory 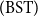$(\mathrm{BST})$ , our minimal extension of Bishop’s theory of sets. With the machinery of the general theory of families of sets, this BHK-interpretation within BST is extended to complex formulas. 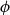Consequently, we can associate to many formulas $\phi$ of BISH a set 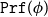${\texttt{Prf}}(\phi)$ of “proofs” or witnesses of 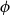$\phi$ . 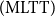Abstracting from several examples of totalities in BISH, we define the notion of a set with a proof-relevant equality, and of a Martin-Löf set, a special case of the former, the equality of which corresponds to the identity type of a type in intensional Martin-Löf type theory $(\mathrm{MLTT})$ . Through the concepts and results of BST notions and facts of MLTT and its extensions (either with the axiom of function extensionality or with Vooevodsky’s axiom of univalence) can be translated into BISH. While Bishop’s theory of sets is standardly understood through its translation to MLTT, our development of BST offers a partial translation in the converse direction.