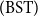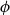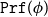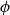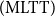Proof-relevance in Bishop-style constructive mathematics

Abstract

Bishop’s presentation of his informal system of constructive mathematics BISH was on purpose closer to the proof-irrelevance of classical mathematics, although a form of proof-relevance was evident in the use of several notions of moduli (of convergence, of uniform continuity, of uniform differentiability, etc.). Focusing on membership and equality conditions for sets given by appropriate existential formulas, we define certain families of proof sets that provide a BHK-interpretation of formulas that correspond to the standard atomic formulas of a first-order theory, within Bishop set theory $(\mathrm{BST})$ , our minimal extension of Bishop’s theory of sets. With the machinery of the general theory of families of sets, this BHK-interpretation within BST is extended to complex formulas. Consequently, we can associate to many formulas $\phi$ of BISH a set ${\texttt{Prf}}(\phi)$ of “proofs” or witnesses of $\phi$ . Abstracting from several examples of totalities in BISH, we define the notion of a set with a proof-relevant equality, and of a Martin-Löf set, a special case of the former, the equality of which corresponds to the identity type of a type in intensional Martin-Löf type theory $(\mathrm{MLTT})$ . Through the concepts and results of BST notions and facts of MLTT and its extensions (either with the axiom of function extensionality or with Vooevodsky’s axiom of univalence) can be translated into BISH. While Bishop’s theory of sets is standardly understood through its translation to MLTT, our development of BST offers a partial translation in the converse direction.

1. On Bishop’s Theory of Sets

The theory of sets underlying Bishop-style constructive mathematics $(\mathrm{BISH})$ was only sketched in Chapter 3 of Bishop’s seminal book (Bishop 1967). Since Bishop’s central aim in Bishop (1967) was to show that a large part of advanced mathematics can be done within a constructive and computational framework that does not contradict the classical practice, the inclusion of a detailed account of the set-theoretic foundations of BISH could possibly be against the effective delivery of his message.

The Bishop-Cheng measure theory, developed in Bishop and Cheng (1972), was very different from the measure theory of Bishop (1967), and the inclusion of an enriched version of the former into Bishop and Bridges (1985), the book on constructive analysis that Bishop co-authored with Bridges later, affected the corresponding Chapter 3 in two main respects. First, the inductively defined notion of the set of Borel sets generated by a given family of complemented subsets ¹ of a set X with respect to a set of real-valued functions on X, was excluded, as unnecessary, and, second, the operations on the complemented subsets of a set X were defined differently, and in accordance to the needs of the new measure theory.

Yet, in both books, many issues were left untouched, a fact that often was a source of confusion. In many occasions, especially in the measure theory of Bishop and Cheng (1972) and Bishop and Bridges (1985), the powerset was treated as a set, while in the measure theory of Bishop (1967), Bishop generally avoided the powerset by using appropriate families of subsets instead. In later works of Bridges and Richman, like Bridges and Richman (1987) and Mines et al. (1988), the powerset was clearly used as a set, in contrast though, to the predicative spirit of Bishop (1967).

The concept of a family of sets indexed by a (discrete) set was asked to be defined in Bishop (1967, Exercise 2, p. 72), and a definition, attributed to Richman, was given in Bishop and Bridges (1985, Exercise 2, p. 78). An elaborate study though, of this concept within BISH, was missing, despite its central character in the measure theory of Bishop (1967), its extensive use in the theory of Bishop spaces (Petrakis 2015a,b, 2016a,b, 2019a,b, 2020a,b, 2021, to appear, 2022a) and in abstract constructive algebra (Mines et al. 1988). Actually, in Mines et al. (1988) Richman introduced the more general notion of a family of objects of a category indexed by some set, but the categorical component in the resulting mixture of Bishop’s set theory and category theory was not explained in constructive terms. ²

The type-theoretic interpretation of Bishop’s set theory into the theory of setoids (see especially the work of Palmgren 2005, 2012a, 2012b, 2013, 2014, 2017; Palmgren and Wilander 2014) has become nowadays the standard way to understand Bishop sets (as far as I know, this is a term due to Palmgren). A setoid is a type A in a fixed universe $\mathcal{U}$ equipped with a term $\simeq \colon A \to A \to \mathcal{U}$ that satisfies the properties of an equivalence relation. The identity type of Martin-Löf’s intensional type theory (MLTT) (see Martin-Löf 1998), expresses, in a proof-relevant way, the existence of the least reflexive relation on a type, a fact with no counterpart in Bishop’s set theory. As a consequence, the free setoid on a type is definable (see Palmgren 2014, p. 90), and the presentation axiom in setoids is provable. Moreover, in MLTT, the families of types over a type I are the type $I \to \mathcal{U}$ , which belongs to the successor universe $\mathcal{U}{'}$ of $\mathcal{U}$ . In Bishop’s set theory though, where only one universe of sets is implicitly used, the set character of the totality of all families of sets indexed by some set I is questionable from the predicative point of view (see our comment after Definition 11).

2. On Bishop Set Theory $(\mathrm{BST})$

Bishop set theory $(\mathrm{BST})$ , elaborated in Petrakis (2020c), is an informal, constructive theory of totalities and assignment routines that serves as a “completion” of Bishop’s theory of sets. Its first aim is to fill in the “gaps,” or highlight the fundamental notions that were suppressed by Bishop in his account of the set theory underlying BISH. Its second aim is to serve as an intermediate step between Bishop’s theory of sets and an adequate and faithful formalisation of BISH in Feferman’s sense (Feferman 1979). To assure faithfulness, we use concepts or principles that appear, explicitly or implicitly, in BISH. Next we describe briefly the features of BST that “complete” Bishop’s theory of sets in Petrakis (2020 c).

1. Explicit use of a universe of sets. Bishop used a universe of sets only implicitly. For example, he “roughly” describes in Bishop (1967), p. 72, a set-indexed family of sets as

$\ldots$ a rule which assigns to each t in a discrete set T a set $\lambda(t)$ .

Every other rule, or assignment routine mentioned by Bishop is from one given totality, the domain of the rule, to some other totality, its codomain. The only way to make the rule of a family of sets compatible with this pattern is to employ a totality of sets. In the unpublished manuscript (Bishop 1968), Bishop explicitly used a universe in his formulation of dependent-type theory as a formal system for BISH. Here we use the totality $\mathbb{V}_0$ of sets, which is defined in an open-ended way, and it contains the primitive set ${\mathbb N}$ and all defined sets. $\mathbb{V}_0$ itself is not a set, but a class. It is a notion instrumental to the definition of dependent operations and of a set-indexed family of sets.

2. Clear distinction between sets and classes. A class is a totality defined through a membership condition in which a quantification over $\mathbb{V}_0$ occurs. The powerset $\mathcal{P}(X)$ of a set X, the totality $\mathcal{P}^{\boldsymbol {\unicode{x27E7}} \boldsymbol {\unicode{x27E6}}}(X)$ of complemented subsets of a set X, and the totality $\mathcal{F}(X,Y)$ of partial functions from a set X to a set Y are characteristic examples of classes. A class is never used here as the domain of an assignment routine, only as a codomain of an assignment routine.

3. Explicit use of dependent operations. The standard view, even among practicioners of Bishop-style constructive mathematicians, is that dependency is not necessary to BISH. Dependent functions though, do appear explicitly in Bishop’s definition of the intersection $\bigcap_{t \in T}\lambda (t)$ of a family $\lambda$ of subsets of some set X indexed by an inhabited set T (see Bishop 1967, p. 65, and Bishop and Bridges 1985, p. 70). As we try to show in Petrakis (2021); Petrakis (2019c) and (2020 c), the elaboration of dependency within BISH is only fruitful to it. Dependent functions are not only necessary to the definition of products of families of sets indexed by an arbitrary set, but in many areas of constructive mathematics. As already mentioned, dependency is formulated in Bishop’s type theory (Bishop 1968). The somewhat “silent” role of dependency within Bishop’s set theory is replaced by a central role within BST.

4. Elaboration of the theory of families of sets. With the use of the universe $\mathbb{V}_0$ , of the notion of a non-dependent assignment routine $\lambda_0$ from an index-set I to $\mathbb{V}_0$ , and of a certain dependent operation $\lambda_1$ , we define explicitly in Definition 11 the notion of a family of sets indexed by I. Although an I-family of sets is a certain function-like object, it can be understood also as an object of a one level higher than that of a set. The corresponding notion of a “function” from an I-family $\Lambda$ to an I-family M is that of a family-map. Operations between sets generate operations between families of sets and their family-maps. If the index-set I is a directed set, the corresponding notion of a family of sets over it is that of a direct family of sets. Families of subsets of a given set X over an index-set I are special I-families that deserve an independent treatment. Families of equivalence classes, families of partial functions, families of complemented subsets, and direct families of subsets are some of the variations of set-indexed families of subsets that are studied in Petrakis (2020 c) with many applications in Bishop-style constructive mathematics.

Here we apply the general theory of families of sets, in order to reveal proof-relevance in BISH. Classical mathematics is proof-irrelevant, as it is indifferent to objects that “witness” a relation or a more complex formula. On the other extreme, Martin-Löf type theory is proof-relevant, as every element of a type A is a proof of the “proposition” A. Bishop’s presentation of BISH was on purpose closer to the proof-irrelevance of classical mathematics, although a form of proof-relevance was evident in the use of several notions of moduli (of convergence, of uniform continuity, of uniform differentiability, etc.). Focusing on membership and equality conditions for sets given by appropriate existential formulas, we define certain families of proof-sets that provide a BHK-interpretation within BST of formulas that correspond to the standard atomic formulas of a first-order theory. With the machinery of the general theory of families of sets, this BHK-interpretation within BST is extended to complex formulas. Consequently, we can associate to many formulas $\phi$ of BISH a set ${\texttt{Prf}}(\phi)$ of “proofs” or witnesses of $\phi$ . Abstracting from several examples of totalities in BISH, we define the notion of a set with a proof-relevant equality, and of a Martin-Löf set, a special case of the former, the equality of which corresponds to the identity type of a type in intensional MLTT. Through the concepts and results of BST notions and facts of MLTT and its extensions (either with the axiom of function extensionality $(\mathrm{FunExt})$ , or with Voevodsky’s axiom of univalence $({\texttt{UA}})$ ) can be translated into BISH. While Bishop’s theory of sets is standardly understood through its translation to MLTT (see e.g., Coquand et al. 2005), the development of BST offers a partial translation in the converse direction.

3. Outline of this Paper

1. (i) In Section 4, we present the fundamental notions of BST that are used in the rest of the paper.

2. (ii) In Section 6, we define within BST the notion of a set-indexed family of sets and its corresponding $\sum$ - and $\prod$ -sets. Moreover, we provide all new set-indexed families of sets constructed from given ones that are used in the following sections.

3. (iii) In Section 7, we define the notion of a set-relevant family of sets, a generalisation of a family of sets over a set with a proof-relevant equality, introduced in Section 11.

4. (iv) In Section 9, we provide a BHK-interpretation of a large part of BISH within BST, including many motivating examples.

5. (v) In Section 10, we present interesting totalities in BISH equipped with a proof-relevant equality.

6. (vi) In Section 11, we introduce the notion of a Martin-Löf set in BST, an abstract version of a set in BST with a proof-relevant equality, and we prove some first fundamental properties of Martin-Löf sets.

7. (vii) In Section 12, we translate results on contractible sets and subsingletons from Homotopy Type Theory into BST.

4. Fundamental Notions of BST

The logical framework of BST is first-order intuitionistic logic with equality (see Schwichtenberg and Wainer 2012, Chapter 1). This primitive equality between terms is denoted by $s := t$ , and it is understood as a definitional, or logical, equality. That is, we read the equality $s := t$ as “the term s is by definition equal to the term t.” If $\phi$ is an appropriate formula, for the standard axiom for equality $[a := b \ \& \ \phi(a)] \Rightarrow \phi(b)$ , we use the notation $[a := b \ \& \ \phi(a)]:\Rightarrow \phi(b)$ . The equivalence notation $:\Leftrightarrow$ is understood in the same way. The set $({\mathbb N} =_{{\mathbb N}}, \neq_{{\mathbb N}})$ of natural numbers, where its canonical equality is given by $m =_{{\mathbb N}} n :\Leftrightarrow m := n$ , and its canonical inequality by $m \neq_{{\mathbb N}} n :\Leftrightarrow \neg(m =_{{\mathbb N}} n)$ , is primitive. The standard Peano-axioms are associated to ${\mathbb N}$ .

A global operation $( \cdot, \cdot)$ of pairing is also considered primitive. That is, if s, t are terms, their pair (s,t) is a new term. The corresponding equality axiom is $(s, t) := (s{'}, t{'}) :\Leftrightarrow s := s{'} \ \& \ t := t{'}$ . The n-tuples of given terms, for every n larger than 2, are definable. The global projection routines ${\textbf{pr}}_1(s, t) := s$ and ${\textbf{pr}}_2(s, t) := t$ are also considered primitive. The corresponding global projection routines for any n-tuples are definable.

An undefined notion of mathematical construction, or algorithm, or of finite routine is considered as primitive. The main primitive objects of BST are totalities and assignment routines. Sets are special totalities and functions are special assignment routines, where an assignment routine is a a special finite routine. All other equalities in BST are equalities on totalities defined though an equality condition. A predicate on a set X is a bounded formula P(x) with x a free variable ranging over X, where a formula is bounded, if every quantifier occurring in it is over a given set.

Definition 1.

1. (i) A primitive set $\mathbb{A}$ is a totality with a given membership $x \in \mathbb{A}$ , and a given equality $x =_{\mathbb{A}} y$ , that satisfies axiomatically the properties of an equivalence relation. The set ${\mathbb N}$ of natural numbers is the only primitive set considered here.

2. (ii) A (noninductive)defined totality X is defined by a membership condition $x \in X : \Leftrightarrow \mathcal{M}_X(x),$ where $\mathcal{M}_X$ is a formula with x as a free variable.

3. (iii) There is a special “open-ended” defined totality $\mathbb{V}_0$ , which is called the universe of (predicative) sets. $\mathbb{V}_0$ is not defined through a membership-condition, but in an open-ended way. When we say that a defined totality X is considered to be a set we “introduce” X as an element of $\mathbb{V}_0$ . We do not add the corresponding induction, or elimination principle, as we want to leave open the possibility of adding new sets in $\mathbb{V}_0$ .

4. (iv) A defined preset X, or simply, a preset, is a defined totality X the membership condition $\mathcal{M}_X$ of which expresses a construction. No quantification over $\mathbb{V}_0$ occurs in $\mathcal{M}_X$ .

5. (v) A defined totality X with equality, or simply, a totality X with equality is a defined totality X equipped with an equality condition $x =_X y : \Leftrightarrow \mathcal{E}_X(x, y)$ , where $\mathcal{E}_X(x,y)$ is a formula with free variables x and y that satisfies the conditions of an equivalence relation.

6. (vi) A defined set is a preset with a given equality.

7. (vii) A set is either a primitive set or a defined set.

8. (viii) A totality is a class, if it is the universe $\mathbb{V}_0$ , or if quantification over $\mathbb{V}_0$ occurs in its membership condition.

Definition 2. A bounded formula on a set X is called an extensional property on X, if

\begin{equation*}\forall_{x, y \in X}\big([x =_{X } y \ \& \ P(x)] \Rightarrow P(y)\big). \end{equation*}

The totality $X_P$ generated by P(x) is defined by $x \in X_P : \Leftrightarrow x \in X \ \& \ P(x)$ ,

\begin{equation*} x \in X_P : \Leftrightarrow x \in X \ \& \ P(x), \end{equation*}

and the equality of $X_P$ is inherited from the equality of X. We also write $X_P := \{x \in X \mid P(x)\}$ , $X_P$ is considered to be a set, and it is called the extensional subset of X generated by P.

Using the properties of an equivalence relation, it is immediate to show that an equality condition $\mathcal{E}_X(x,y)$ on a totality X is an extensional property on the product $X \times X$ , i.e., $[(x, y) =_{X \times Y} (x{'}, y{'}) \ \&\ x =_X y] \Rightarrow x{'} =_X y{'}$ . Let the following extensional subsets of ${\mathbb N}$ :

\begin{equation*} \pmb{1} := \{x \in {\mathbb N} \mid x =_{{\mathbb N}} 0\} := \{0\}, \end{equation*}

\begin{equation*} \pmb{2} := \{x \in {\mathbb N} \mid x =_{{\mathbb N}} 0 \ \vee x =_{{\mathbb N}} 1\} := \{0, 1\}. \end{equation*}

Since $n =_{{\mathbb N}} m :\Leftrightarrow n := m$ , the property $P(x) :\Leftrightarrow x =_{{\mathbb N}} 0 \ \vee x =_{{\mathbb N}} 1$ is extensional.

Definition 3. If $(X, =_X)$ is a set, its diagonal is the extensional subset of $X \times X$

\begin{equation*} D(X, =_X) := \{(x, y) \in X \times X \mid x =_X y\}. \end{equation*}

If $=_X$ is clear from the context, we just write D(X).

Definition 4. Let X, Y be totalities. A nondependent assignment routine f from X to Y, in symbols $f \colon X \rightsquigarrow Y$ , is a finite routine that assigns an element y of Y to each given element x of X. In this case, we write $f(x) := y$ . If $g \colon X \rightsquigarrow Y$ , let

\begin{equation*}f := g : \Leftrightarrow \forall_{x \in X}\big(f(x) := g(x)\big). \end{equation*}

If $f := g$ , we say that f and g are definitionally equal. If $(X, =_X)$ and $(Y, =_Y)$ are sets, an operation from X to Y is a nondependent assignment routine from X to Y, while a function from X to Y, in symbols $f \colon X \to Y$ , is an operation from X to Y that respects equality, i.e.,

\begin{equation*}\forall_{x, x{'} \in X}\big(x =_X x{'} \Rightarrow f(x) =_Y f(x{'})\big). \end{equation*}

If $f \colon X \rightsquigarrow Y$ is a function from X to Y, we say that f is a function, without mentioning the expression “from X to Y.” A function $f \colon X \to Y$ is an embedding, in symbols $f \colon X \hookrightarrow Y$ , if

\begin{equation*}\forall_{x, x{'} \in X}\big( f(x) =_Y f(x{'}) \Rightarrow x =_X x{'}). \end{equation*}

Let X, Y be sets. The totality $\mathbb{O}(X, Y)$ of operations from X to Y is equipped with the following canonical equality:

\begin{equation*} f =_{\mathbb{O}(X, Y)} g : \Leftrightarrow \forall_{x \in X}\big(f(x) =_Y f(x)\big). \end{equation*}

The totality $\mathbb{O}(X, Y)$ is considered to be a set. The set $\mathbb{F}(X, Y)$ of functions from X to Y is defined by separation on $\mathbb{O}(X, Y)$ through the extensional property $P(f) :\Leftrightarrow \forall_{x, x{'} \in X}\big(x =_X x{'} \Rightarrow f(x) =_Y f(x{'})\big)$ . The equality $=_{\mathbb{F}(X, Y)}$ is inherited from $=_{\mathbb{O}(X, Y)}$ .

The canonical equality on $\mathbb{V}_0$ is defined by

\begin{equation*} X =_{\mathbb{V}_0} Y :\Leftrightarrow \exists_{f \in \mathbb{F}(X,Y)}\exists_{g \in \mathbb{F}(Y,X)}\big(g \circ f = \mathrm{id}_X \ \& f \circ g = \mathrm{id}_Y\big).\end{equation*}

In this case, we write $(f, g) : X =_{\mathbb{V}_0} Y$ . If $X, Y \in \mathbb{V}_0$ such that $X =_{\mathbb{V}_0} Y$ , we define the set

\begin{equation*} {\texttt{PrfEql}}_0(X, Y) := \big\{(f, g) \in \mathbb{F}(X, Y) \times \mathbb{F}(Y, X) \mid (f, g) : X =_{\mathbb{V}_0} Y\big\} \end{equation*}

of all objects that “witness,” or “realise,” or prove the equality $X =_{\mathbb{V}_0} Y$ . The equality of ${\texttt{PrfEql}}_0(X, Y)$ is the canonical one, i.e., $(f, g) =_{{\texttt{PrfEql}}_0(X, Y)} (f{'}, g{'}) :\Leftrightarrow f =_{\mathbb{F}(X, Y)} f{'} \ \&\ g =_{\mathbb{F}(Y, X)}g{'}$ . Notice that, in general, not all elements of ${\texttt{PrfEql}}_0(X, Y)$ are equal. As in The Univalent Foundations Program (2013), Example 3.1.9, if $X := Y := \pmb{2} := \{0, 1\}$ , then $(\mathrm{id}_{\pmb{2}}, \mathrm{id}_{\pmb{2}}) \in{\texttt{PrfEql}}_0(\pmb{2}, \pmb{2})$ , and if ${\texttt{sw}}_{\pmb{2}} : \pmb{2} \to \pmb{2}$ maps 0 to 1 and 1 to 0, then $({\texttt{sw}}_{\pmb{2}}, {\texttt{sw}}_{\pmb{2}})\in {\texttt{PrfEql}}_0(\pmb{2}, \pmb{2})$ , while ${\texttt{sw}}_{\pmb{2}} \neq \mathrm{id}_{\pmb{2}}$ .

It is expected that the proof-terms in ${\texttt{PrfEql}}_0(X, Y)$ are compatible with the properties of the equivalence relation $X =_{\mathbb{V}_0} Y$ . This means that we can define a distinguished proof-term ${\texttt{refl}}(X) \in {\texttt{PrfEql}}_0(X, X)$ that proves the reflexivity of $X =_{\mathbb{V}_0} Y$ , an operation -1, such that if $(f, g) : X =_{\mathbb{V}_0} Y$ , then $(f, g)^{-1} : Y =_{\mathbb{V}_0} X$ , and an operation of “composition” $\ast$ of proof-terms, such that if $(f, g) : X =_{\mathbb{V}_0} Y$ and $(h, k) : Y =_{\mathbb{V}_0} Z$ , then $(f, g) \ast (h, k) :X =_{\mathbb{V}_0} Z$ . Let

\begin{equation*}{\texttt{refl}}(X) := \big(\mathrm{id}_X, \mathrm{id}_X\big) \ \ \& \ \ (f, g)^{-1} := (g, f) \ \ \& \ \ (f, g) \ast (h, k) := (h \circ f, g \circ k).\end{equation*}

It is immediate to see that these operations satisfy the groupoid laws:

${\texttt{refl}} (X) \ast (f, g) =_{{\texttt{PrfEql}}_0(X, Y)} (f, g)$ and $(f, g) \ast {\texttt{refl}} (Y) =_{{\texttt{PrfEql}}_0(X, Y)} (f, g)$ .

$(f, g) \ast (f, g)^{-1} =_{{\texttt{PrfEql}}_0(X, X)} {\texttt{refl}} (X)$ and $(f, g)^{-1} \ast (f, g) =_{{\texttt{PrfEql}}_0(Y, Y)} {\texttt{refl}} (Y)$ .

$\big((f, g) \ast (h, k)\big) \ast (s, t) =_{{\texttt{PrfEql}}_0(X, W)} (f, g) \ast \big((h, k) \ast (s, t)\big)$ .

Moreover, the following compatibility condition is satisfied:

If $(f, g), (f{'}, g{'}) \in {\texttt{PrfEql}}_0(X, Y)$ and $(h, k), (h{'}, k{'}) \in {\texttt{PrfEql}}_0(Y, Z)$ , then if $(f, g) =_{{\texttt{PrfEql}}_0(X, Y)} (f{'}, g{'})$ and $(h, k) =_{{\texttt{PrfEql}}_0(Y, Z)} (h{'}, k{'})$ , then $(f, g) \ast (h, k) =_{{\texttt{PrfEql}}_0(X, Z)} (f{'}, g{'}) \ast (h{'}, k{'})$ .

Definition 5. Let $(X, =_X)$ be a set.

1. (i) X is inhabited, if $\exists_{x \in X}\big(x =_X x\big)$ .

2. (ii) X is a singleton, or contractible, or a $(-2)$ -set, if $\exists_{x_0 \in X}\forall_{x \in X}\big(x_0 =_{\small{X}} x\big)$ . In this case, $x_0$ is called a centre of contraction for X.

3. (iii) X is a subsingleton, or a mere proposition, or a $(-1)$ -set, if $\forall_{x, y \in X}\big(x =_{\small{X}} y\big)$ .

4. (iv) The truncation of $(X, =_X)$ is the set $(X, {\small{\small{\lvert \lvert =_X \rvert \rvert}}})$ , where

   \begin{equation*} x \ \small{\small{\lvert \lvert =_X \rvert \rvert}} \ y :\Leftrightarrow x =_X x \ \& \ y =_X y. \end{equation*}
   We use the symbol $||X||$ to denote that the set X is equipped with the truncated equality $\small{\small{\lvert \lvert =_X \rvert \rvert}}$ .

Clearly, $ x \ \small{\small{\lvert \lvert =_X \rvert \rvert}} \ y$ , for every $x, y \in X$ , and $(X, \small{\small{\lvert \lvert =_X \rvert \rvert}})$ is a subsingleton.

Definition 6. A function $f \colon X \to Y$ is called surjective, if $\forall_{y \in Y}\exists_{x \in X}\big(f(x) =_Y y\big)$ . A function $g \colon Y \to X$ is called a modulus of surjectivity for f, if $f \circ g =_{\mathbb{F}(Y,Y)} \mathrm{id}_Y$ . If g is a modulus of surjectivity for f, we also say that f is a retraction and Y is a retract of X. If $y \in Y$ , the fiber ${\texttt{fib}}^f(y)$ of f at y is the following extensional subset of X

\begin{equation*} {\texttt{fib}}^f(y) := \{x \in X \mid f(x) =_Y y \}. \end{equation*}

A function $f \colon X \to Y$ is contractible, if ${\texttt{fib}}^f(y)$ is contractible, for every $y \in Y$ .

Proposition 7. Let X, Y be sets, $f \in \mathbb{F}(X, Y)$ and $g \in \mathbb{F}(Y,X)$ . If $(f, g) \colon X =_{\mathbb{V}_0} Y$ , then the set ${\texttt{fib}}^f(y)$ is contractible, for every $y \in Y$ .

Proof. If $y \in Y$ , then $g(y) \in {\texttt{fib}}^f(y)$ , as $f(g(y)) =_Y \mathrm{id}_Y(y) := y$ . If $x \in X$ , $x \in {\texttt{fib}}^f(y) :\Leftrightarrow f(x) =_Y y$ , and $x =_X g(f(x)) =_X g(y)$ , i.e., g(y) is a center of contraction for ${\texttt{fib}}^f(y)$ .

Definition 8. Let I be a set and $\lambda_0 \colon I \rightsquigarrow \mathbb{V}_0$ a nondependent assignment routine from I to $\mathbb{V}_0$ . A dependent operation $\Phi$ over $\lambda_0$ , in symbols

is an assignment routine that assigns to each element i in I an element $\Phi(i)$ in the set $\lambda_0(i)$ . If $i \in I$ , we call $\Phi(i)$ the i-component of $\Phi$ , and we also use the notation $\Phi_i := \Phi(i)$ An assignment routine is either a nondependent assignment routine or a dependent operation over some nondependent assignment routine from a set to the universe. If

, $\Phi := \Psi :\Leftrightarrow \forall_{i \in I}\big(\Phi_i := \Psi_i\big).$ If $\Phi := \Psi$ , we say that $\Phi$ and $\Psi$ are definitionally equal. Let $\mathbb{A}(I, \lambda_0)$ be the totality of dependent operations over $\lambda_0$ , equipped with the canonical equality $\Phi =_{\mathbb{A}(I, \lambda_0)} \Psi :\Leftrightarrow \forall_{i \in I}\big(\Phi_i=_{\lambda_0(i)} \Psi_i\big)$ . The totality $\mathbb{A}(I, \lambda_0)$ is considered to be a set.

If $f \colon X \to Y$ , let ${\texttt{fib}}^f \colon Y \rightsquigarrow \mathbb{V}_0$ be defined by $y \mapsto {\texttt{fib}}^f(y)$ , for every $y \in Y$ . If f is contractible, then by Definition 6 every fiber ${\texttt{fib}}^f(y)$ of f is contractible. A modulus of centers of contraction for a contractible function f is a dependent operation , such that ${\texttt{centre}}^f_y := {\texttt{centre}}^f(y)$ is a center of contraction for f.

5. Subsets

Definition 9. Let X be a set. A subset of X is a pair $(A, i_A^X)$ , where A is a set and $1_A^X \colon A \hookrightarrow X$ is an embedding. If $(A, i_A^X)$ and $(B, i_B^X)$ are subsets of X, then A is a subset of B, in symbols $(A, i_A^X) \subseteq (B, i_B^X)$ , or simpler $A \subseteq B$ , if there is $f \colon A \to B$ such that the following diagram commutes

In this case we use the notation $f \colon A \subseteq B$ . Usually we write A instead of $(A, i_A^X)$ . The totality of the subsets of X is the powerset $\mathcal{P}(X)$ of X, and it is equipped with the equality

\begin{equation*} (A, i_A^X) =_{\mathcal{P}(X)} (B, i_B^X) :\Leftrightarrow A \subseteq B \ \& \ B \subseteq A. \end{equation*}

If $f \colon A \subseteq B$ and $g \colon B \subseteq A$ , we write $(f, g) \colon A =_{\mathcal{P}(X)} B$ .

Since the membership condition for $\mathcal{P}(X)$ requires quantification over $\mathbb{V}_0$ , the totality $\mathcal{P}(X)$ is a class. Clearly, $(X, \mathrm{id}_X) \subseteq X$ . If $X_P$ is an extensional subset of X (see Definition 2), then $(X_P, i_P^X) \subseteq X$ , where $i_P^X \colon X_P \rightsquigarrow X$ is defined by $i_P^X(x) := x$ , for every $x \in X_P$ .

Proposition 10. If $A, B \subseteq X$ , and $f, h : A \subseteq B$ , then f is an embedding, and $f =_{\mathbb{F}(A, B)} h$

Proof. If $a, a{'} \in A$ such that $f(a) =_B f(a{'})$ , then $i_B^X(f(a)) =_X i_B^X(f(a{'})) \Leftrightarrow i_A^X(a) =_X i_A^X (a{'})$ , which implies $a =_A a{'}$ . Moreover, if $i_B^X(f(a)) =_X i_A^X(a) =_X i_B^X(h(a))$ , then $f(a) = h(a)$ .

The “internal” equality of subsets implies their “external” equality as sets, i.e., $(f, g) : A =_{\mathcal{P}(X)} B \Rightarrow (f, g) : A =_{\mathbb{V}_0} B$ . If $a \in A$ , then $i_A^X(g(f(a))) =_X i_B^X(f(a)) = i_A^X (a)$ , hence $g(f(a)) =_A a$ , and then $g \circ f =_{\mathbb{F}(A, A)} \mathrm{id}_A$ . Similarly, we get $f \circ g =_{\mathbb{F}(B, B)} \mathrm{id}_B$ . Let the set

\begin{equation*} {\texttt{PrfEql}}_0(A, B) := \big\{(f, g) \in \mathbb{F}(A, B) \times \mathbb{F}(B, A) \mid f \colon A \subseteq B \ \& \ g\colon B \subseteq A\big\}, \end{equation*}

equipped with the canonical equality of pairs as in the case of ${\texttt{PrfEql}}_0(X, Y)$ . Because of Proposition 10, the set ${\texttt{PrfEql}}_0(A, B)$ is a subsingleton, i.e.,

\begin{equation*} (f, g) \colon A =_{\mathcal{P}(X)} B \ \& \ (f{'}, g{'}) \colon A =_{\mathcal{P}(X)} B \Rightarrow (f, g) = (f{'}, g{'}). \end{equation*}

If $f \in \mathbb{F}(A, B), g \in \mathbb{F}(B, A), h \in \mathbb{F}(B, C)$ , and $k \in \mathbb{F}(C, B)$ , let ${\texttt{refl}}(A) := \big(\mathrm{id}_A, \mathrm{id}_A\big)$ and $(f, g)^{-1} := (g, f)$ , and $(f, g) \ast (h, k) := (h \circ f, g \circ k)$ , and the groupoid properties (i)–(iv) for ${\texttt{PrfEql}}_0(A, B)$ hold by the equality of all their elements.

6. Set-Indexed Families of Sets

Roughly speaking, a family of sets indexed by some set I is an assignment routine $\lambda_0 : I \rightsquigarrow \mathbb{V}_0$ that behaves like a function i.e., if $i =_I j$ , then $\lambda_0(i) =_{\mathbb{V}_0} \lambda_0 (j)$ . Next follows an exact formulation of this description that reveals the witnesses of the equality $\lambda_0(i) =_{\mathbb{V}_0} \lambda_0 (j)$ .

Definition 11. If I is a set, a family of sets indexed by I, or an I-family of sets, is a pair $\Lambda := (\lambda_0, \lambda_1)$ , where $\lambda_0 \colon I \rightsquigarrow \mathbb{V}_0$ , and $\lambda_1$ , a modulus of function-likeness for $\lambda_0$ , is given by

such that the transport maps $\lambda_{ij}$ of $\Lambda$ satisfy the following conditions:

1. (a) For every $i \in I$ , we have that $\lambda_{ii} := \mathrm{id}_{\lambda_0(i)}$ .

2. (b) If $i =_I j$ and $j =_I k$ , the following diagram commutes

I is the index-set of the family $\Lambda$ . If X is a set, the constant I-family of sets X is the pair $C^X := (\lambda_0^X, \lambda_1^X)$ , where $\lambda_0 (i) := X$ , for every $i \in I$ , and $\lambda_1 (i, j) := \mathrm{id}_X$ , for every $(i, j) \in D(I)$ . The pair $\Lambda^{\pmb{2}} := (\lambda_0^{\pmb{2}}, \lambda_1^{\pmb{2}})$ , where $\lambda_0^{\pmb{2}} \colon \pmb{2} \rightsquigarrow \mathbb{V}_0$ with $\lambda_0^{\pmb{2}} (0) := X$ , $\lambda_0^{\pmb{2}} (1) := Y$ , and $\lambda_1^{\pmb{2}} (0, 0) := \mathrm{id}_X$ and $\lambda_1^{\pmb{2}} (1, 1) := \mathrm{id}_Y$ , is the $\pmb{2}$ -family of X and Y. The $\pmb{n}$ -family $\Lambda^{\pmb{n}}$ of the sets $X_1, \ldots X_n$ , where $n \geq 1$ , and the ${\mathbb N}$ -family $\Lambda^{{\mathbb N}} := (\lambda_0^{{\mathbb N}}, \lambda_1^{{\mathbb N}})$ of the sets $(X_n)_{n \in {\mathbb N}}$ are defined similarly. Let $\Lambda := (\lambda_0, \lambda_1)$ and $M := (\mu_0, \mu_1)$ be I-families of sets. A family-map from $\Lambda$ to M, in symbols $\Psi \colon \Lambda\Rightarrow M$ is a dependent operation such that for every $(i, j) \in D(I)$ the following diagram commutes

Let ${\texttt{Map}}_I(\Lambda, M)$ be the totality of family-maps from $\Lambda$ to M, which is equipped with the equality

\begin{equation*} \Psi =_{{\texttt{Map}}_I(\Lambda, M)} \Xi :\Leftrightarrow \forall_{i \in I}\big(\Psi_i =_{\mathbb{F}(\lambda_0(i), \mu_0(i))}\Xi_i\big). \end{equation*}

The composition family-map and the identity family-map $\mathrm{Id}_{\Lambda}$ are defined in the expected way. Let ${\texttt{Fam}}(I)$ be the totality of I-families, equipped with the canonical equality

\begin{equation*} \Lambda =_{{\texttt{Fam}}(I)} M :\Leftrightarrow\exists_{\Phi \in {\texttt{Map}}_I(\Lambda, M)}\exists_{\Xi \in {\texttt{Map}}_I(M, \Lambda)}\big((\Phi, \Xi) \colon\Lambda =_{{\texttt{Fam}}(I)} M\big), \end{equation*}

\begin{equation*} (\Phi, \Xi) \colon \Lambda =_{{\texttt{Fam}}(I)} M :\Leftrightarrow \big(\Phi \circ \Xi = \mathrm{id}_M \ \& \ \Xi \circ \Phi = \mathrm{id}_{\Lambda}\big).\end{equation*}

The dependent operation $\lambda_1$ in the definition of an I-family of sets should have been written as

but, for simplicity, we avoid the use of the primitive projections ${\textbf{pr}}_1, {\textbf{pr}}_2$ . Condition (a) of Definition 11 could have been written as $\lambda_{ii}=_{\small{\mathbb{F}(\lambda_0(i),\lambda_0(i))}} \mathrm{id}_{\lambda_0(i)}$ . If $i =_I j$ , then by conditions (b) and (a) of Definition 11 we get $id_{\lambda_0(i)} := \lambda_{ii} = \lambda_{ji} \circ \lambda_{ij}$ and $ \mathrm{id}_{\lambda_0(j)} := \lambda_{jj} = \lambda_{ij} \circ \lambda_{ji} $ , i.e., $(\lambda_{ij}, \lambda_{ji}) \colon \lambda_0 (i) =_{\mathbb{V}_0} \lambda_0 (j)$ . In this sense, $\lambda_1$ is a modulus of function-likeness for $\lambda_0$ . It is natural to accept the totality ${\texttt{Map}}(\Lambda, M)$ as a set. If ${\texttt{Fam}}(I)$ was a set though, the constant I-family with value ${\texttt{Fam}}(I)$ would be defined though a totality in which it belongs to. From a predicative point of view, this cannot be accepted. The membership condition of the totality ${\texttt{Fam}}(I)$ though does not depend on the universe $\mathbb{V}_0$ , therefore it is also natural not to consider ${\texttt{Fam}}(I)$ to be a class. Hence, ${\texttt{Fam}}(I)$ is a totality “between” a (predicative) set and a class. For this reason, we say that ${\texttt{Fam}}(I)$ is an impredicative set.

Definition 12. Let $\Lambda := (\lambda_0, \lambda_1), M := (\mu_0, \mu_1)$ be I-families of sets.

1. (i) The product family of $\Lambda$ and M is the pair $\Lambda \times M := (\lambda_0 \times \mu_0, \lambda_1 \times \mu_1)$ , where

   \begin{equation*} (\lambda_0 \times \mu_0)(i) := \lambda_0 (i) \times \mu_0 (i); \ \ \ \ i \in I, \end{equation*}
   \begin{equation*} \big(\lambda_1 \times \mu_1\big)_{ij} \colon \lambda_0 (i) \times \mu_0 (i) \to \lambda_0 (j)\times \mu_0 (j);\ \ \ (i, j) \in D(I), \end{equation*}
   \begin{equation*} \big(\lambda_1 \times \mu_1\big)_{ij}\big(x, y\big) := \big(\lambda_{ij}(x), \mu_{ij}(y)\big); \ \ \ x \in \lambda_0 (i) \ \& \ y \in \mu_0 (i). \end{equation*}

2. (ii) The function space family from $\Lambda$ to M is the pair $\mathbb{F}(\Lambda, M) := \big(\mathbb{F}(\lambda_0, \mu_0), \mathbb{F}(\lambda_1, \mu_1)\big)$ where

   \begin{equation*} \big[\mathbb{F}(\lambda_0, \mu_0)\big](i) := \mathbb{F}\big(\lambda_0(i), \mu_0(i)\big); \ \ \ \ i \in I, \end{equation*}
   
   \begin{equation*} \mathbb{F}(\lambda_1, \mu_1)_{ij} := \mathbb{F}(\lambda_1, \mu_1)(i, j) \colon \mathbb{F}\big(\lambda_0(i), \mu_0(i)\big) \to \mathbb{F}\big(\lambda_0(j), \mu_0(j)\big); \ \ \ \ (i, j) \in D(I), \end{equation*}
   \begin{equation*} \mathbb{F}(\lambda_1, \mu_1)_{ij}(f) := \mu_{ij} \circ f \circ \lambda_{ji} \end{equation*}

Definition 13. Let $\Lambda := (\lambda_0, \lambda_1)$ be an I-family of sets. The exterior union, or disjoint union, or the $\sum$ -set $\sum_{i \in I}\lambda_0 (i)$ of $\Lambda$ , and its canonical equality are defined by

\begin{equation*} w \in \sum_{i \in I}\lambda_0 (i) :\Leftrightarrow \exists_{i \in I}\exists_{x \in \lambda_0 (i)}\big(w := (i, x)\big), \end{equation*}

\begin{equation*} (i, x) =_{\small{\sum_{i \in I}\lambda_0 (i)}} (j, y) : \Leftrightarrow i =_I j \ \& \ \lambda_{ij} (x)=_{\lambda_0 (j)} y. \end{equation*}

The $\sum$ -set of the $\pmb{2}$ -family $\Lambda^{\pmb{2}}$ of the sets X and Y is the coproduct of X and Y, and we write

\begin{equation*} X + Y := \sum_{i \in \pmb{2}}\lambda_0^{\pmb{2}}(i). \end{equation*}

Let $\Lambda := (\lambda_0, \lambda_1), M := (\mu_0, \mu_1)$ be I-families of sets. The coproduct family of $\Lambda$ and M is the pair $\Lambda + M := (\lambda_0 + \mu_0, \lambda_1 + \mu_1)$ , where $(\lambda_0 + \mu_0)(i):= \lambda_0 (i) + \mu_0 (i)$ , for every $i \in I$ , and the map $\big(\lambda_1 + \mu_1\big)_{ij} \colon \lambda_0 (i) +\mu_0 (i) \to \lambda_0 (j) + \mu_0 (j)$ is defined by

\begin{equation*} \big(\lambda_1 + \mu_1\big)_{ij}(w) := \left\{ \begin{array}{ll} \big(0, \lambda_{ij}(x)\big) &\mbox{, $w := (0, x)$}\\ \big(1, \mu_{ij}(y)\big) &\mbox{, $w := (1, y)$} \end{array} \right.; \ \ \ \ w \in \lambda_0 (i) + \mu_0 (i). \end{equation*}

Definition 14. Let $\Lambda := (\lambda_0, \lambda_1)$ be an I-family of sets. The first projection on $\sum_{i \in I}\lambda_0 (i)$ is the operation ${\texttt{pr}}_1^{\Lambda} \colon \sum_{i \in I}\lambda_0 (i) \rightsquigarrow I$ , defined by $pr_1^{\Lambda} (i, x) : = {\textbf{pr}}_1 (i, x) := i$ , for every $(i, x) \in\sum_{i \in I}\lambda_0 (i)$ . We write ${\texttt{pr}}_1$ , if $\Lambda$ is clearly understood from the context.

By the definition of the canonical equality on $\sum_{i \in I}\lambda_0 (i)$ , we get that ${\texttt{pr}}_1^{\Lambda}$ is a function.

Definition 15. Let $\Lambda := (\lambda_0, \lambda_1)$ be an I-family of sets. The $\sum$ -indexing of $\Lambda$ is the pair $\Sigma^{\Lambda} := (\sigma_0^{\Lambda}, \sigma_1^{\Lambda})$ , where $\sigma_0^{\Lambda}\colon \sum_{i \in I}\lambda_0 (i) \rightsquigarrow \mathbb{V}_0$ is defined by $\sigma_0^{\Lambda}(i, x) := \lambda_0(i)$ , for every $(i, x) \in \sum_{i \in I}\lambda_0 (i)$ , and $\sigma_1^{\Lambda}\big((i,x),(j,y)\big) := \lambda_{ij}$ , for every $\big((i,x),(j,y)\big) \in D\big(\sum_{i \in I}\lambda_0 (i)\big)$ .

Clearly, $\Sigma^{\Lambda}$ is a family of sets over $\sum_{i \in I}\lambda_0 (i)$ .

Definition 16. Let $\Lambda := (\lambda_0, \lambda_1)$ be an I-family of sets. The second projection on $\sum_{i \in I}\lambda_0 (i)$ is the dependent operation , defined by ${\texttt{pr}}_2^{\Lambda}(i,x) := {\textbf{pr}}_2(i,x) := x$ , for every $(i, x) \in \sum_{i \in I}\lambda_0 (i)$ . We write ${\texttt{pr}}_2$ , when the family of sets $\Lambda$ is clearly understood from the context.

Definition 17. Let $\Lambda := (\lambda_0, \lambda_1)$ be an I-family of sets. The totality $\prod_{i \in I}\lambda_0(i)$ of dependent functions over $\Lambda$ , or the $\prod$ -set of $\Lambda$ , is defined by

\begin{equation*}\Theta \in \prod_{i \in I}\lambda_0(i) :\Leftrightarrow \Theta \in \mathbb{A}(I, \lambda_0) \ \& \forall_{(i,j) \in D(I)}\big(\Theta_j=_{\lambda_0(j)} \lambda_{ij}(\Theta_i)\big),\end{equation*}

and it is equipped with the canonical equality and the canonical inequality of the set $\mathbb{A}(I, \lambda_0)$ . If X is a set and $\Lambda^X$ is the constant I-family X (see Definition 11), we use the notation

\begin{equation*} X^I := \prod_{i \in I}X. \end{equation*}

Remark 18. If $\Lambda := (\lambda_0, \lambda_1)$ is an I-family of sets and $\Sigma^{\Lambda} := (\sigma_0^{\Lambda}, \sigma_1^{\Lambda})$ is the $\sum$ -indexing of $\Lambda$ , then ${\texttt{pr}}_2^{\Lambda}$ is a dependent function over $\Sigma^{\Lambda}$ .

Proof. By Definition 16 the second projection ${\texttt{pr}}_2^{\Lambda}$ of $\Lambda$ is the dependent assignment , such that ${\texttt{pr}}_2^{\Lambda}(i,x) := x$ , for every $(i, x) \in \sum_{i \in I}\lambda_0 (i)$ . It suffices to show that if $(i, x) =_{\small{\sum_{i \in I}\lambda_0 (i)}} (j, y) : \Leftrightarrow i =_I j \ \& \ \lambda_{ij} (x)=_{\lambda_0 (j)} y$ , then

\begin{equation*} {\texttt{pr}}_2^{\Lambda}(j,y) := y=_{\lambda_0 (j)} \lambda_{ij} (x):= \sigma_1^{\Lambda}\big((i,x),(j,y)\big)\big({\texttt{pr}}_2^{\Lambda}(i,x)\big).\end{equation*}

Next we define new families of sets generated by a given family of sets indexed by the product $X \times Y$ of X and Y.

Definition 19. Let X, Y be sets, and let $R := (\rho_0, \rho_1)$ be an $(X \times Y)$ -family of sets.

1. (i) If $x \in X$ , the x-component of R is the pair $R^x := (\rho_0^x, \rho_1^x)$ , where the assignment routines $\rho_0^x \colon Y \rightsquigarrow \mathbb{V}_0$ and are defined by $\rho_0^x(y) := \rho_0(x, y)$ , for every $y \in Y$ , and $\rho_1^x (y, y{'}) := \rho_{yy{'}}^x := \rho_{(x,y)(x,y{'})}$ , for every $(y, y{'}) \in D(Y)$ .

2. (ii) If $y \in Y$ , the y-component of R is the pair $R^y := (\rho_0^y, \rho_1^y)$ , where the assignment routines $\rho_0^y \colon Y \rightsquigarrow \mathbb{V}_0$ and are defined by $\rho_0^y(x) := \rho_0(x, y)$ , for every $x \in X$ , and $\rho_1^y (x, x{'}) := \rho_{xx{'}}^y := \rho_{(x,y)(x{'},y)}$ , for every $(x, x{'}) \in D(X)$ .

3. (iii) Let $\sum^1R := (\sum^1 \rho_0, \sum^1 \rho_1)$ , where $\sum^1 \rho_0 : X \rightsquigarrow \mathbb{V}_0$ and

   
   \begin{equation*} \bigg(\sum^1 \rho_0\bigg) (x) := \sum_{y \in Y}\rho_0^x(y) := \sum_{y \in Y}\rho_0(x, y); \; x \in X, \end{equation*}
   \begin{equation*} \bigg(\sum^1 \rho_1\bigg) (x, x{'}) := \bigg(\sum^1 \rho_1\bigg)_{xx{'}} \colon\sum_{y \in Y}\rho_0 (x, y) \to \sum_{y \in Y}\rho_0 (x{'}, y); \ \ \ (x, x{'}) \in D(X), \end{equation*}
   \begin{equation*} \bigg(\sum^1 \rho_1\bigg)_{xx{'}}(y, u) := \big(y, \rho_{(x, y)(x{'},y)}(u)\big); \ \ \ \ (y, u) \in\sum_{y \in Y}\rho_0 (x, y). \end{equation*}

4. (iv) Let $\sum^2R := (\sum^2 \rho_0, \sum^2 \rho_1)$ , where $\sum^2 \rho_0 : Y \rightsquigarrow \mathbb{V}_0$ and

   
   \begin{equation*} \bigg(\sum^2 \rho_0\bigg) (y) := \sum_{x \in X}\rho_0^y(x) := \sum_{x \in X}\rho_0(x, y); \; y \in Y, \end{equation*}
   \begin{equation*} \bigg(\sum^2 \rho_1\bigg) (y, y{'}) := \bigg(\sum^2 \rho_1\bigg)_{yy{'}} \colon\sum_{x \in X}\rho_0 (x, y) \to \sum_{x \in X}\rho_0 (x, y{'}); \ \ \ (y, y{'}) \in D(Y), \end{equation*}
   \begin{equation*} \bigg(\sum^2 \rho_1\bigg)_{yy{'}}(x, w) := \big(x, \rho_{(x, y)(x,y{'})}(w)\big); \ \ \ \ (x, w) \in\sum_{x \in X}\rho_0 (x, y). \end{equation*}

5. (v) Let $\prod^1R := (\prod^1 \rho_0, \prod^1 \rho_1)$ , where $\prod^1 \rho_0 : X \rightsquigarrow \mathbb{V}_0$ and

   
   \begin{equation*} \bigg(\prod^1 \rho_0\bigg) (x) := \prod_{y \in Y}\rho_0^x(y) := \prod_{y \in Y}\rho_0(x, y); \;\; x \in X, \end{equation*}
   \begin{equation*} \bigg(\prod^1 \rho_1\bigg) (x, x{'}) := \bigg(\prod^1 \rho_1\bigg)_{xx{'}} \colon\prod_{y \in Y}\rho_0 (x, y) \to \prod_{y \in Y}\rho_0 (x{'}, y); \ \ \ (x, x{'}) \in D(X), \end{equation*}
   \begin{equation*} \bigg[\bigg(\prod^1 \rho_1\bigg)_{xx{'}}(\Theta)\bigg]_y := \rho_{(x, y)(x{'},y)}(\Theta_y)\big); \;\;\; \Theta \in\prod_{y \in Y}\rho_0 (x, y), \ y \in Y. \end{equation*}

6. (vi) Let $\prod^2R := (\prod^2 \rho_0, \prod^2 \rho_1)$ , where $\prod^2 \rho_0 : Y \rightsquigarrow \mathbb{V}_0$ and

   
   \begin{equation*} \bigg(\prod^2 \rho_0\bigg) (y) := \prod_{x \in X}\rho_0^y(x) := \prod_{x \in X}\rho_0(x, y); \;\;\;\; y \in Y, \end{equation*}
   \begin{equation*} \bigg(\prod^2 \rho_1\bigg) (y, y{'}) := \bigg(\prod^2 \rho_1\bigg)_{yy{'}} \colon\prod_{x \in X}\rho_0 (x, y) \to \prod_{x \in X}\rho_0 (x, y{'}); \ \ \ (y, y{'}) \in D(Y), \end{equation*}
   \begin{equation*} \bigg[\bigg(\prod^2 \rho_1\bigg)_{yy{'}}(\Phi)\bigg]_x := \rho_{(x, y)(x,y{'})}(\Phi_x)\big); \;\;\;\; \Phi \in\prod_{x \in X}\rho_0 (x, y), \ x \in X. \end{equation*}

It is easy to show that $R^y, \sum^1R, \prod^1R \in {\texttt{Fam}}(X)$ and $R^x, \sum^2R, \prod^2R \in {\texttt{Fam}}(Y)$ .

7. Set-Relevant Families of Sets

In general, we may want to have more than one transport maps from $\lambda_0(i)$ to $\lambda_0(j)$ , if $i =_I j$ . In this case, to each $(i, j) \in D(I)$ we associate a set of transport maps.

Definition 20. If I is a set, a set-relevant family of sets indexed by I, is a triplet $\Lambda^* := \big(\lambda_0, \varepsilon_0^{\lambda}, \lambda_2)$ , where $\lambda_0 : I \rightsquigarrow \mathbb{V}_0$ , $\varepsilon_0^{\lambda} : D(I) \rightsquigarrow \mathbb{V}_0$ , and

such that the following conditions hold:

1. (i) For every $i \in I$ there is $p \in \varepsilon_0^{\lambda}(i, i)$ such that $\lambda_{ii}^p=_{\mathbb{F}(\lambda_0(i), \lambda_0(i))} \mathrm{id}_{\lambda_0(i)}$ .

2. (ii) For every $(i, j) \in D(I)$ and every $p \in \varepsilon_0^{\lambda}(i, j)$ there is some $q \in \varepsilon_0^{\lambda}(j, i)$ such that the following left diagram commutes

1. (iii) If $i =_I j =_I k$ , then for every $p \in \varepsilon_0^{\lambda}(i, j)$ and every $q \in \varepsilon_0^{\lambda}(j, k)$ there is $r \in \varepsilon_0^{\lambda}(i, k)$ such that the above right diagram commutes.

We call $\Lambda^*$ function-like, if $ \forall_{(i, j) \in D(I)}\forall_{p, p{'} \in\varepsilon_0^{\lambda}(i, j)}\big( p =_{\varepsilon_0^{\lambda}(i, j)} p{'} \Rightarrow \lambda_{ij}^p =_{\mathbb{F}(\lambda_0(i), \lambda_0(j))} \lambda_{ij}^{p{'}}\big)$ .

It is immediate to show that if $\Lambda := (\lambda_0, \lambda_1) \in {\texttt{Fam}}(I)$ , then $\Lambda$ generates a set-relevant family over I, where $\varepsilon_0^{\lambda}(i,j) := \pmb{1}$ , and $\lambda_2\big((i,j), 0)\big) := \lambda_{ij}$ , for every $(i,j) \in D(I)$ .

Definition 21. Let $\Lambda^* := (\lambda_0, \varepsilon_0^{\lambda}, \lambda_2)$ and $M := (\mu_0,\varepsilon_0^{\mu}, \mu_2)$ be set-relevant families of sets over I. A covariant set-relevant family-map from $\Lambda^*$ to $M^*$ , in symbols $\Psi \colon \Lambda^* \Rightarrow M^*$ , is a dependent operation such that for every $(i, j) \in D(I)$ and for every $p \in \varepsilon_0^{\lambda}(i, j)$ there is $q \in \varepsilon_0^{\mu}(i,j)$ such that the following diagram commutes

A contravariant set-relevant family-map is defined by the property: for every $q \in \varepsilon_0^{\mu}(i,j)$ , there is $p \in \varepsilon_0^{\lambda}(i, j)$ such that the above diagram commutes. Let ${\texttt{Map}}_I(\Lambda^*, M^*)$ be the totality of covariant set-relevant family-maps from $\Lambda^*$ to $M^*$ , which is equipped with the pointwise equality. If $\Xi : M^* \Rightarrow N^*$ , the composition set-relevant family-map $\Xi \circ \Psi \colon \Lambda^* \Rightarrow N^*$ is defined, for every $i \in I$ , by $(\Xi \circ \Psi)_i := \Xi_i \circ \Psi_i$ . Let ${\texttt{Fam}}^*(I)$ be the totality of set-relevant I-families, equipped with the obvious canonical equality.

Definition 22. Let $\Lambda^* := \big(\lambda_0, \varepsilon_0^{\lambda}, \lambda_2\big) \in {\texttt{Fam}}^*(I)$ . The exterior union $\sum_{i \in I}^*\lambda_0(i)$ of $\Lambda^*$ is the totality $\sum_{i \in I} \lambda_0 (i)$ , equipped with the following equality

\begin{equation*} (i, x) =_{\sum_{i \in I}^* \lambda_0 (i)} (j, y) : \Leftrightarrow i =_I j \ \& \ \exists_{p \in\varepsilon_0^{\lambda} (i, j)}\big(\lambda_{ij}^p (x) =_{\lambda_0 (j)} y\big). \end{equation*}

The totality $\prod_{i \in I}^*\lambda_0(i)$ of dependent functions over $\Lambda^*$ is defined by

\begin{equation*} \Theta \in \prod_{i \in I}^*\lambda_0(i) :\Leftrightarrow \Theta \in \mathbb{A}(I, \lambda_0)\ \& \ \forall_{(i,j) \in D(I)}\forall_{p \in \varepsilon_0^{\lambda}(i,j)}\big(\Theta_j=_{\lambda_0(j)} \lambda_{ij}^p(\Theta_i)\big), \end{equation*}

and it is equipped with the pointwise equality.

A motivation for the definitions of $\sum^*_{i \in I}\lambda_0(i)$ and $\prod_{i \in I}^*\lambda_0(i)$ is provided, respectively, by Theorem 2.7.2 of book-HoTT (The Univalent Foundations Program 2013), where if $w, w{'}\in \sum_{i \colon I}P(i)$ , then

\begin{equation*} w = w{'} \simeq \sum_{p \colon {\texttt{pr}}_1(w) = {\texttt{pr}}_1(w{'})}p_{\ast}({\texttt{pr}}_2(w)) = {\texttt{pr}}_2(w{'}), \end{equation*}

and by Lemma 2.3.4 of book-HoTT, where if $\Phi \colon \prod_{i \in I}P(i)$ , there is a term

\begin{equation*} {\texttt{apd}}_{\Phi} \colon \prod_{p \colon i = j}\big(p_{\ast}(\Phi_i) = \Phi_j\big). \end{equation*}

8. Set-Indexed Families of Subsets

Roughly speaking, a family of subsets of a set X indexed by some set I is an assignment routine $\lambda_0 : I \rightsquigarrow \mathcal{P}(X)$ that behaves like a function, i.e., if $i =_I j$ , then $\lambda_0(i) =_{\mathcal{P}(X)}\lambda_0 (j)$ . The following definition is a formulation of this rough description that reveals the witnesses of the equality $\lambda_0(i) =_{\mathcal{P}(X)} \lambda_0 (j)$ . This is done “internally,” through the embeddings of the subsets into X. The equality $\lambda_0(i) =_{\mathbb{V}_0} \lambda_0 (j)$ , which in the previous chapter is defined “externally” through the transport maps, follows, and a family of subsets is also a family of sets.

Definition 23. Let X and I be sets. A family of subsets of X indexed by I, or an I-family of subsets of X, is a triplet $\Lambda(X) := (\lambda_0, \mathcal{E}^X, \lambda_1)$ , where $\lambda_0 : I \rightsquigarrow \mathbb{V}_0$ ,

such that the following conditions hold:

1. (a) For every $i \in I$ , the function $\mathcal{E}_i^X : \lambda_0(i) \to X$ is an embedding.

2. (b) For every $i \in I$ , we have that $\lambda_{ii} := \mathrm{id}_{\lambda_0(i)}$ .

3. (c) For every $(i, j) \in D(I)$ , we have that $\mathcal{E}_i^X = \mathcal{E}_j^X \circ \lambda_{ij}$ and $\mathcal{E}_j^X = \mathcal{E}_i^X \circ \lambda_{ji}$

$\mathcal{E}^X$ is a modulus of embeddings for $\lambda_0$ , and $\lambda_1$ a modulus of transport maps for $\lambda_0$ . Let $\Lambda := (\lambda_0, \lambda_1)$ be the I-family of sets that corresponds to $\Lambda(X)$ . If $(A, i_A) \in \mathcal{P}(X)$ , the constant I-family of subsets A is the pair $C^{A}(X) := (\lambda_0^{A}, \mathcal{E}^{X,A}, \lambda_1^A)$ , where $\lambda_0 (i) := A$ , $\mathcal{E}_i^{X,A} := i_A$ , and $\lambda_1 (i, j) := \mathrm{id}_A$ , for every $i \in I$ and $(i, j) \in D(I)$ (see the left diagram in Definition 25).

Proposition 24. Let X and I be sets, $\lambda_0 : I \rightsquigarrow \mathbb{V}_0$ , $\mathcal{E}^X$ a modulus of embeddings for $\lambda_0$ , and $\lambda_1$ a modulus of transport maps for $\lambda_0$ . The following are equivalent.

1. (i) $\Lambda(X) := (\lambda_0, \mathcal{E}^X, \lambda_1)$ is an I-family of subsets of X.

2. (ii) $\Lambda := (\lambda_0, \lambda_1) \in {\texttt{Fam}}(I)$ and $\mathcal{E}^X \colon \Lambda \Rightarrow C^X$ , where $C^X$ is the constant I-family X.

Proof. (i) $\Rightarrow$ (ii) First, we show that $\Lambda \in {\texttt{Fam}}(I)$ . If $i =_I j =_I k$ , then $\mathcal{E}_k^X \circ (\lambda_{jk} \circ \lambda_{ij}) = (\mathcal{E}_k^X \circ \lambda_{jk}) \circ \lambda_{ij}= \mathcal{E}_j^X \circ \lambda_{ij} = \mathcal{E}_i^X$ and $\mathcal{E}_k^X \circ \lambda_{ik} = \mathcal{E}_i^X$

hence $\mathcal{E}_k^X \circ (\lambda_{jk} \circ \lambda_{ij}) = \mathcal{E}_k^X \circ \lambda_{ik}$ , and since $\mathcal{E}_k^X$ is an embedding, we get $\lambda_{jk} \circ \lambda_{ij} = \lambda_{ik}$ . If $\mathcal{E}^X \colon \Lambda \Rightarrow C^X$ , the following squares are commutative

if and only if the above triangles are commutative. The implication (ii) $\Rightarrow$ (i) follows immediately from the equivalence between the commutativity of the above pairs of diagrams.

Definition 25. Let X be a set and $(A, i_A^X), (B, i_B^X) \subseteq X$ . The triplet $\Lambda^{\pmb{2}}(X) := (\lambda_0^{\pmb{2}}, \mathcal{E}^X, \lambda_1^{\pmb{2}})$ , where $\Lambda^{\pmb{2}} := \lambda_0^{\pmb{2}}, \lambda_1^{\pmb{2}}$ is the $\pmb{2}$ -family of A, B, $\mathcal{E}^X_0 := i_A^X$ , and $\mathcal{E}^X_1 := i_B^X$

is the $\pmb{2}$ -family of subsets A and B of X. The ${\textbf{n}}$ -family $\Lambda^{{\textbf{n}}}(X)$ of the subsets $(A_1, i_1), \ldots, (A_n, i_n)$ of X, and the ${\mathbb N}$ -family of subsets $(A_n, i_n)_{n \in {\mathbb N}}$ of X are defined similarly.

Definition 26. If $\Lambda(X) := (\lambda_0, \mathcal{E}^X, \lambda_1), M(X) := (\mu_0, \mathcal{Z}^X, \mu_1)$ and $N(X) := (\nu_0, \mathcal{H}^X, \nu_1)$ are I-families of subsets of X, a family of subsets-map $\Psi \colon \Lambda(X) \Rightarrow M(X)$ from $\Lambda(X)$ to M(X) is a dependent operation , where $\Psi(i) := \Psi_i$ , for every $i \in I$ , such that, for every $i \in I$ , the following diagram commutes

The totality ${\texttt{Map}}_I(\Lambda(X), M(X))$ of family of subsets-maps from $\Lambda(X)$ to M(X) is equipped with the pointwise equality. If $\Psi \colon \Lambda(X) \Rightarrow M(X)$ and $\Xi \colon M(X) \Rightarrow N(X)$ , the composition family of subsets-map $\Xi \circ \Psi \colon \Lambda(X) \Rightarrow N(X)$ is defined by $(\Xi \circ \Psi)(i) := \Xi_i \circ \Psi_i$ ,

for every $i \in I$ . The identity family of subsets-map $\mathrm{Id}_{\Lambda(X)} \colon \Lambda(X) \Rightarrow \Lambda(X)$ is defined, as expected.

Definition 27. If $\Lambda(X), M(X) \in {\texttt{Fam}}(I, X)$ , let $\Lambda(X) \leq M(X)$ , if there is a family of subsets-map $\Phi \colon \Lambda(X) \Rightarrow M(X)$ . In this case, we also write $\Phi \colon \Lambda(X) \leq M(X)$ . Let $\Phi \in {\texttt{Map}}_I(\Lambda(X), M(X)), \Psi \in {\texttt{Map}}_I(M(X), \Lambda(X)),\Phi{'} \in {\texttt{Map}}_I(M(X), N(X))$ , $\Psi{'} \in {\texttt{Map}}_I(N(X), M(X))$ . Then we define

\begin{equation*}{\texttt{PrfEql}}_0(\Lambda(X), M(X)) := {\texttt{Map}}_I(\Lambda(X), M(X)) \times {\texttt{Map}}_I(M(X), \Lambda(X))\end{equation*}

i.e., $(\Phi, \Psi) \colon \Lambda(X) =_{{\texttt{Fam}}(I, X)} M(X) :\Leftrightarrow \Phi \colon \ \Lambda(X) \leq M(X) \ \& \ \Psi \colon M(X) \leq \Lambda(X)$ . Moreover, let ${\texttt{refl}}(\Lambda(X)) := \big(\mathrm{Id}_{\Lambda(X)}, \mathrm{Id}_{\Lambda(X)}\big)$ , $(\Phi, \Psi)^{-1} := (\Psi, \Phi)$ , and $(\Phi, \Psi) \ast (\Phi{'}, \Psi{'}) :=(\Phi{'} \circ \Phi, \Psi \circ \Psi{'})$ .

We see no obvious reason, like the one for ${\texttt{Fam}}(I)$ , not to consider ${\texttt{Fam}}(I, X)$ to be a set. In the case of ${\texttt{Fam}}(I)$ , the constant I-family ${\texttt{Fam}}(I)$ would be in ${\texttt{Fam}}(I)$ , while the constant I-family ${\texttt{Fam}}(I, X)$ is not clear how could be seen as a family of subsets of X. If $\nu_0(i) := {\texttt{Fam}}(I, X)$ , for every $i \in I$ , we need to define a modulus of embeddings $\mathcal{N}^X_i \colon {\texttt{Fam}}(I, X)\hookrightarrow X$ , for every $i \in I$ . From the given data one could define the assignment routine $\mathcal{N}^X_i$ by the rule $\mathcal{N}^X_i\big(\Lambda(X)\big) := \mathcal{E}_i^X(u_i)$ , if it is known that $u_i \in \lambda_0(i)$ . Even in that case, the assignment routine $\mathcal{N}^X_i$ cannot be shown to satisfy the expected properties. Clearly, if $\mathcal{N}^X_i$ was defined by the rule $\mathcal{N}^X_i\big(\Lambda(X)\big) := x_0 \in X$ , then it cannot be an embedding.

Proposition 28. Let $\Lambda(X) := (\lambda_0, \mathcal{E}^X, \lambda_1), M(X) := (\mu_0, \mathcal{Z}^X, \mu_1) \in {\texttt{Fam}}(I, X)$ .

1. (i) If $\Psi \colon \Lambda(X) \Rightarrow M(X)$ , then $\Psi \colon \Lambda \Rightarrow M$ .

2. (ii) If $\Psi \colon \Lambda(X) \Rightarrow M(X)$ and $\Phi \colon \Lambda(X) \Rightarrow M(X)$ , then $\Phi =_{{\texttt{Map}}_I(\Lambda(X), M(X))} \Psi$ .

Proof.

1. (i) By the commutativity of the following inner diagrams

we get the required commutativity of the above outer diagram. If $x \in \lambda_0(i)$ , then

\begin{equation*} (\mathcal{Z}_j^X \circ \Psi_j)\big(\lambda_{ij}(x)\big)= \mathcal{E}_j^X \big(\lambda_{ij}(x)\big) = \mathcal{E}_i^X (x) = (\mathcal{Z}_i^X \circ \Psi_i)(x) = \mathcal{Z}_j^X\big(\mu_{ij}(\Psi_i (x))\big). \end{equation*}

Since $\mathcal{Z}_j^X \big(\Psi_j (\lambda_{ij}(x))\big) = \mathcal{Z}_j^X\big(\mu_{ij}(\Psi_i (x))\big)$ , we get $\Psi_j (\lambda_{ij}(x) = \mu_{ij}(\Psi_i (x))$ .

1. (ii) If $i \in I$ , then $\Psi_i \colon \lambda_0(i) \subseteq \mu_0(i)$ , $\Phi_i \colon \lambda_0(i) \subseteq \mu_0(i)$

hence by Proposition 10 we get $\Psi_i =_{\mathbb{F}(\lambda_0(i), \mu_0(i))} \Phi_i$ .

Because of Proposition 28(ii) all the elements of ${\texttt{PrfEql}}_0(\Lambda(X), M(X))$ are equal to each other, hence the groupoid properties (i)-(iv) for ${\texttt{PrfEql}}_0(\Lambda(X), M(X))$ hold trivially. Of course, $\Lambda(X) =_{{\texttt{Fam}}(I, X)} M(X) :\Leftrightarrow \Lambda(X) \leq M(X) \ \& \ M(X) \leq \Lambda(X)$ .

9. On the BHK-interpretation of BISH within BST

In the next naive definition of the BHK-interpretation of BISH, the notion of “proof” is not understood in the proof-theoretic sense. Although we agree with Streicher in Streicher (2018) that the term “witness” is better, we use the symbol ${\texttt{Prf}}(\phi)$ for traditional reasons. We could have used the symbol ${\texttt{Wtn}}(\phi)$ instead. We choose not to reduce the rule for $\phi \vee \psi$ to the other ones, as for example is done in Beeson (1981), p. 156. The rule for $\neg \phi$ is usually reduced to the rule for implication.

Definition 29. (Naive BHK-interpretation of BISH) Let $\phi, \psi$ be formulas in BISH, such that it is understood what it means “q is a proof (or witness, or evidence) of $\phi$ ” and “r is a proof of $\psi$ .”

$(\wedge)$ A proof of $\phi \wedge \psi$ is a pair $(p_0, p_1)$ such that $p_0$ is a proof of $\phi$ and $p_1$ is a proof of $\psi$ .

$(\Rightarrow)$ A proof of $\phi \Rightarrow \psi$ is a rule r that associates to any proof p of $\phi$ a proof r(p) of $\psi$ .

$(\vee)$ A proof of $\phi \vee \psi$ is a pair $(i, p_i)$ , where if $i := 0$ , then $p_0$ is a proof of $\phi$ , and if $i := 1$ , then $p_1$ is a proof of $\psi$ .

$(\bot)$ There is no proof of $\bot$ .

For the next two rules let $\phi(x)$ be a formula on a set X, such that it is understood what it means “q is a proof of $\phi(x)$ ,” for every $x \in X$ .

$(\forall)$ A proof of $\forall_{x \in X}\phi(x)$ is a rule R that associates to any given $x \in X$ a proof $R_x$ of $\phi(x)$ .

$(\exists)$ A proof of $\exists_{x \in X}\phi(x)$ is a pair (x, q), where $x \in X$ and q is a proof of $\phi(x)$ .

The notions of “rule” in the clauses for $(\Rightarrow)$ and $(\forall)$ are unclear. The nature of a proof or a witness is also unclear. The interpretation of atomic formulas is also not included. In Aczel and Rathjen (2010, p. 12), the following criticism to the naive BHK-interpretation is given:

Many objections can be raised against the above definition. The explanations offered for implication and universal quantification are notoriously imprecise because the notion of function (or rule) is left unexplained. Another problem is that the notions of set and set membership are in need of clarification. But in practice, these rules suffice to codify the arguments that mathematicians want to call constructive. Note also that the above interpretation (except for $\bot$ ) does not address the case of atomic formulas.

A formal version of the above naive BHK-interpretation of BISH is a corresponding realisability interpretation (see Section 13). Following Feferman (1979), Beeson declared in Beeson (1981, p. 158) that “the fundamental relation in constructive set theory is not membership but membership-with-evidence” $(\mathrm{MwE})$ . All examples given by Feferman are certain extensional subsets of some set X. In MLTT, this kind of $(\mathrm{MwE})$ is captured by the type $\sum_{x : A} P(x)$ , where $P \colon A \to \mathcal{U}$ is a family of types over $A \colon \mathcal{U}$ . Here we explain how we can talk about $(\mathrm{MwE})$ for extensional subsets of some set X within BST, showing that BISH, as MLTT, is capable of expressing $(\mathrm{MwE})$ . As all such examples known to us are extensional subsets, we do not consider the notion of a completely presented set $X^*$ , for every set X, as it is done in the formal systems $T_0^*$ of Feferman in Feferman (1979), and in Beeson’s system, found in Beeson (1981). In the system of Beeson (1981), proof-relevance is even more stressed, as to any formula $\phi$ a formula ${\texttt{Prf}}_{\phi}(p)$ is associated by a certain rule, expressing that “p proves formula $\phi$ .” The resulting formal set theory though, is, in our opinion, not attractive. The problem of the totality of proofs being a definite preset, hence the problem of quantifying over it (see Beeson 1981, p. 177) is solved by our “internal” treatment of MwE within BST. Consequently, questionable principles, like Beeson’s “ $(\mathrm{MwE})$ is self-evident” (see Beeson 1981, p. 159), are avoided.

Proposition 30. (Membership-with-Evidence I (MwE-I)) Let X, Y be sets, and let P(x) be a property on X of the form

\begin{equation*} P(x) :\Leftrightarrow \exists_{p \in Y}\big(Q(x, p)\big), \end{equation*}

where Q(x, p) is an extensional property on $X \times Y$ i.e., $\big[x =_X x{'} \ \& \ p =_Y p{'} \ \& \ Q(x, p)\big] \Rightarrow Q(x{'}, p{'}),$ for every $x, x{'} \in X$ and every $p, p{'} \in Y$ . Let ${\texttt{PrfMemb}}^P_0 : X \rightsquigarrow \mathbb{V}_0$ , defined by

\begin{equation*} {\texttt{PrfMemb}}^P_0 (x) := \{p \in Y \mid Q(x, p)\}, \end{equation*}

for every $x \in X$ , and let , where ${\texttt{PrfMemb}}^P_{xx{'}} := {\texttt{PrfMemb}}^P_1(x, x{'}) : {\texttt{PrfMemb}}^P_0(x) \to {\texttt{PrfMemb}}^P_0(x{'})$ is defined by the identity map-rule ${\texttt{PrfMemb}}^P_{xx{'}}(p) := p$ , for every $p \in {\texttt{PrfMemb}}^P_0(x)$ and every $(x, x{'}) \in D(X)$ .

1. (i) The property P(x) is extensional.

2. (ii) The pair ${\texttt{PrfMemb}}^P := \big({\texttt{PrfMemb}}^P_0, {\texttt{PrfMemb}}^P_1\big) \in {\texttt{Fam}}(X)$ .

Proof.

1. (i) Let $x =_X x{'}$ and $p \in Y$ such that Q(x, p). Since $p =_Y p$ , by the extensionality of Q we get Q(x’, p), and hence P(x’).

2. (ii) First we show that the dependent operation ${\texttt{PrfMemb}}^P_1$ is well defined. If $x =_X x{'}$ and $p \in {\texttt{PrfMemb}}^P_0 (x)$ , i.e., Q(x, p), by the extensionality of Q, we get Q(x’, p). Clearly, the operation ${\texttt{PrfMemb}}^P_{xx{'}}$ is a function. As ${\texttt{PrfMemb}}^P_{xx{'}}$ is given by the identity map rule, the properties of a family of sets for ${\texttt{PrfMemb}}^P_1$ are trivially satisfied.

Actually, ${\texttt{PrfMemb}}^P$ can be seen as a family of subsets of Y over X, but now we want to work externally, and not internally. ³ For the previous result, it suffices to suppose that Q is X-extensional, i.e., $\big[x =_X x{'} \ \& \ Q(x, p)\big] \Rightarrow Q(x{'}, p)$ , for every $x, x{'} \in X$ and every $p \in Y$ . Notice that the extensionality of P alone does not imply neither the X-extensionality of Q nor the extensionality of Q, and it is not enough to define a function from $ {\texttt{PrfMemb}}^P_0(x)$ to ${\texttt{PrfMemb}}^P_0(x{'})$ . If $X_P$ is the extensional subset of X generated by P, we write $ p : x \in X_P :\Leftrightarrow Q(x, p)$ . The following proposition follows immediately from (MwE-I).

Proposition 31. (Membership-with-Evidence II (MwE-II)) Let X, Y, Z be sets, and let R(x) be a property on X of the form

\begin{equation*} R(x) :\Leftrightarrow \exists_{p \in Y}\exists_{q \in Z}\big(Q(x, p, q)\big), \end{equation*}

where Q(x, p, q) is an extensional property on $X \times Y \times Z$ , i.e., $\big[x =_X x{'} \ \& \ p =_Y p{'} \ \& \ q =_Z q{'} \ \& \ Q(x, p, q)\big] \Rightarrow Q(x{'}, p{'}, q{'})$ , for every $x, x{'} \in X$ , $p, p{'} \in Y$ , and every $q, q{'} \in Y$ . Let ${\texttt{PrfMemb}}^R_0 : X \rightsquigarrow \mathbb{V}_0$ , defined by the rule

\begin{equation*} {\texttt{PrfMemb}}^R_0 (x) := \{(p, q) \in Y \times Z \mid Q(x, p, q)\}, \end{equation*}

for every $x \in X$ , and let , where

\begin{equation*}{\texttt{PrfMemb}}^R_{xx{'}} := {\texttt{PrfMemb}}^R_1(x, x{'}) : {\texttt{PrfMemb}}^R_0(x) \to {\texttt{PrfMemb}}^R_0(x{'}),\end{equation*}

\begin{equation*} {\texttt{PrfMemb}}^R_{xx{'}}(p, q) := (p, q); \ \ \ \ (p, q) \in {\texttt{PrfMemb}}^R_0(x), \ (x, x{'}) \in D(X).\end{equation*}

1. (i) The property R(x) is extensional.

2. (ii) The pair ${\texttt{PrfMemb}}^R := \big({\texttt{PrfMemb}}^R_0, {\texttt{PrfMemb}}^R_1\big) \in {\texttt{Fam}}(X)$ .

Again, ${\texttt{PrfMemb}}^R$ can be seen as a family of subsets of Y over X. If $X_R$ is the extensional subset of X generated by R, we write

\begin{equation*} (p, q) : x \in X_R :\Leftrightarrow Q(x, p, q).\end{equation*}

Clearly, the schema MwE-II can be generalised to a property S(x) on X of the form

\begin{equation*} S(x) :\Leftrightarrow \exists_{p_1 \in X_1} \ldots \exists_{p_n \in X_n}\big(T(x, p_1, \ldots, p_n)\big),\end{equation*}

for some extensional property $T(p_1, \ldots, p_n)$ on $X_1 \times \ldots \times X_n$ . The following scheme of defining functions on extensional subsets of sets given by existential formulas is immediate to prove.

Proposition 32. Let X, Y, X’, Y’ be sets, and let P(x) and P(x’) properties on X and X’, respectively, of the form

\begin{equation*} P(x) :\Leftrightarrow \exists_{p \in Y}\big(Q(x, p)\big) \ \ \ \ \& \ \ \ \ P{'}(x{'}) :\Leftrightarrow\exists_{p{'} \in Y{'}}\big(Q{'}(x{'}, p{'})\big), \end{equation*}

where Q(x, p) and Q’(x’, p’) are extensional properties on $X \times Y$ and on $X{'} \times Y{'}$ , respectively.

1. (i) Let $f \colon X \rightsquigarrow X{'}$ and . Then the operation $f_{PP{'}} \colon X_P \rightsquigarrow X{'}_{P{'}}$ , defined by the rule $X_P \ni x\mapsto f(x) \in X{'}_{P{'}},$ is well defined. If f is a function, then $f_{PP{'}}$ is a function.

2. (ii) Let $g \colon X \rightsquigarrow X{'}$ and . Then the operation $g_{P{'}} \colon X \rightsquigarrow X{'}_{P{'}}$ , defined by the rule $X \ni x\mapsto g(x) \in X{'}_{P{'}},$ is well defined. If g is a function, then $g_{P{'}}$ is a function.

The schemata MwE-I and MwE-II are useful when a mathematical concept is defined as a property on a given set, and not as an element of the set together with some extra data. For example, in Bishop and Bridges (1985, p. 38), and in Bishop (1967, p. 34), a function $f : [a, b] \to {\mathbb R}$ is called continuous, if there is a function $\omega_f \colon {\mathbb R}^+ \to {\mathbb R}^+$ , where ${\mathbb R}^+$ is the set of positive real numbers, such that

\begin{equation*} \forall_{\varepsilon > 0}\forall_{x, y \in [a, b]}\big(|x-y| \leq \omega_f(\varepsilon) \Rightarrow|f(x) - f(y)|\leq \varepsilon\big) :\Leftrightarrow \omega_f \colon {\texttt{Cont}}(f). \end{equation*}

It is also mentioned that the function $\omega$ , the so-called modulus of (uniform) continuity of f is “an indispensable part of the definition of a continuous function.’. The same concept can be defined though, through a property on the set $\mathbb{F}([a, b]) = \mathbb{F}\big([a, b], {\mathbb R}\big)$ , given by an existential formula, i.e.,

\begin{equation*} {\texttt{Cont}}(f) :\Leftrightarrow \exists_{\omega_f \in \mathbb{F}\big( {\mathbb R}^+, {\mathbb R}^+\big)}\big(\omega_f \colon {\texttt{Cont}}(f)\big). \end{equation*}

It is this kind of definition of a mathematical notion that facilitates the definition of a set of witnesses to the membership condition of an extensional subset of a set.

Example 9.1 (Convergent sequences at $x \in {\mathbb R}$ ) Let $X := \mathbb{F}(\mathbb{N}, \mathbb{R})$ , $Y := \mathbb{F}({\mathbb N}^+, {\mathbb N}^+)$ . If $x \in {\mathbb R}$ , let, for every $(x_n)_{n \in{\mathbb N}} \in \mathbb{F}(\mathbb{N}, \mathbb{R})$

\begin{equation*} \mathrm{Conv}_{x}\big((x_n)_{n \in {\mathbb N}}\big) :\Leftrightarrow\exists_{C \in \mathbb{F}({\mathbb N}^+, {\mathbb N}^+)}\big(C \colon x_n \stackrel{n} \longrightarrow x\big), \end{equation*}

\begin{equation*} C \colon x_n \stackrel{n} \longrightarrow x :\Leftrightarrow\forall_{k \in {\mathbb N}^+}\forall_{n \geq C(k)}\bigg(|x_n - x|\leq \frac{1}{k}\bigg). \end{equation*}

If $C \colon x_n \stackrel{n} \longrightarrow$ , we say that C is a modulus of convergence of $(x_n)_{n \in {\mathbb N}}$ at $x \in {\mathbb R}$ .

By the compatibility of the operation minus;, the function $|.|$ , and the relation $\leq$ with the equality of ${\mathbb R}$ , we get the extensionality of

\begin{equation*}Q_x\big((x_n)_{n \in {\mathbb N}}, C) :\Leftrightarrow C : x_n \stackrel{n}\longrightarrow x\end{equation*}

on $\mathbb{F}(\mathbb{N}, \mathbb{R}) \times \mathbb{F}({\mathbb N}^+, {\mathbb N}^+),$ as

\begin{equation*} \big[(x_n)_{n \in {\mathbb N}} =_{\small{\mathbb{F}({\mathbb N}^+, {\mathbb N}^+)}} (y_n)_{n \in {\mathbb N}} \ \& \ C\colon x_n \stackrel{n}\longrightarrow x\big] \Rightarrow C \colon y_n \stackrel{n} \longrightarrow x. \end{equation*}

By Proposition 30 ${\texttt{PrfMemb}}^{\mathrm{Conv}_{x}} := \big({\texttt{PrfMemb}}^{\mathrm{Conv}_{x}}_0, {\texttt{PrfMemb}}^{\mathrm{Conv}_{x}}_1\big) \in {\texttt{Fam}}\big(\mathbb{F}(\mathbb{N},\mathbb{R})\big)$ , where

\begin{equation*} {\texttt{PrfMemb}}^{\mathrm{Conv}_{x}}_0\big((x_n)_{n \in {\mathbb N}}\big) := \big\{C \in \mathbb{F}({\mathbb N}^+, {\mathbb N}^+) \mid C \colon x_n \stackrel{n} \longrightarrow x\big)\big\}. \end{equation*}

Example 9.2. (Cauchy sequences) If $X := \mathbb{F}(\mathbb{N}, \mathbb{R})$ , $Y := \mathbb{F}({\mathbb N}^+, {\mathbb N}^+)$ , $(x_n)_{n \in {\mathbb N}} \in \mathbb{F}(\mathbb{N}, \mathbb{R})$ , let

\begin{equation*} \mathrm{Cauchy}\big((x_n)_{n \in {\mathbb N}}\big) :\Leftrightarrow\exists_{C \in \mathbb{F}({\mathbb N}^+, {\mathbb N}^+)}\big(C \colon \mathrm{Cauchy}\big((x_n)_{n \in {\mathbb N}}\big),\end{equation*}

\begin{equation*} C \colon \mathrm{Cauchy}\big((x_n)_{n \in {\mathbb N}}\big) :\Leftrightarrow \forall_{k \in {\mathbb N}^+}\forall_{n, m\geq C(k)}\bigg(|x_n - x_m|\leq \frac{1}{k}\bigg). \end{equation*}

If $C \colon \mathrm{Cauchy}\big((x_n)_{n \in {\mathbb N}}\big)$ , we say that C is a modulus of Cauchyness for $(x_n)_{n \in {\mathbb N}}$ .

The extensionality of $R\big((x_n)_{n \in {\mathbb N}}, C) :\Leftrightarrow\mathrm{Cauchy}\big((x_n)_{n \in {\mathbb N}}\big)$ follows as above. By Proposition 30 ${\texttt{PrfMemb}}^{\mathrm{Cauchy}} := \big({\texttt{PrfMemb}}^{\mathrm{Cauchy}}_0, {\texttt{PrfMemb}}^{\mathrm{Cauchy}}_1\big) \in {\texttt{Fam}}\big(\mathbb{F}(\mathbb{N}, \mathbb{R})\big)$ , where

\begin{equation*} {\texttt{PrfMemb}}^{\mathrm{Cauchy}}_0\big((x_n)_{n \in {\mathbb N}}\big) := \big\{C \in \mathbb{F}({\mathbb N}^+, {\mathbb N}^+) \mid C \colon \mathrm{Cauchy}\big((x_n)_{n \in {\mathbb N}}\big)\big\}. \end{equation*}

Example 9.3 (Convergent sequences) If $X := \mathbb{F}(\mathbb{N}, \mathbb{R})$ , $Y := {\mathbb R}$ , $Z := \mathbb{F}({\mathbb N}^+, {\mathbb N}^+)$ , $(x_n)_{n \in {\mathbb N}} \in \mathbb{F}(\mathbb{N}, \mathbb{R})$ , let

\begin{equation*} \mathrm{Conv} \big((x_n)_{n \in {\mathbb N}}\big) :\Leftrightarrow\exists_{x \in {\mathbb R}}\exists_{C \in \mathbb{F}({\mathbb N}^+, {\mathbb N}^+)}\big((x, C) \colon\mathrm{Conv} \big((x_n)_{n \in {\mathbb N}}\big).\end{equation*}

\begin{equation*} (x, C) \colon \mathrm{Conv} \big((x_n)_{n \in {\mathbb N}} :\Leftrightarrow \big(C \colon x_n \stackrel{n} \longrightarrow x\big),\end{equation*}

If $(x, C) \colon \mathrm{Conv}\big((x_n)_{n \in {\mathbb N}}\big)$ , we say that (x, C) is a modulus of convergence of $(x_n)_{n \in {\mathbb N}}$ .

The extensionality of $S\big((x_n)_{n \in {\mathbb N}}, x, C) :\Leftrightarrow C \colon x_n \stackrel{n} \longrightarrow x$ on $\mathbb{F}(\mathbb{N}, \mathbb{R}) \times {\mathbb R} \times\mathbb{F}({\mathbb N}^+, {\mathbb N}^+)$ follows from the compatibility of convergence with equality, i.e.,

\begin{equation*} \big[(x_n)_{n \in {\mathbb N}} =_{\small{\mathbb{F}({\mathbb N}^+, {\mathbb N}^+)}} (y_n)_{n \in {\mathbb N}} \ \& \ x =_{{\mathbb R}} y\ \& \ C \colon x_n \stackrel{n} \longrightarrow x\big] \Rightarrow C \colon y_n \stackrel{n} \longrightarrow y. \end{equation*}

By Proposition 31 ${\texttt{PrfMemb}}^{\mathrm{Conv}} := \big({\texttt{PrfMemb}}^{\mathrm{Conv}}_0, {\texttt{PrfMemb}}^{\mathrm{Conv}}_1\big) \in {\texttt{Fam}}(\mathbb{F}(\mathbb{N}, \mathbb{R})\big)$ , where

\begin{equation*} {\texttt{PrfMemb}}^{\mathrm{Conv}}_0\big((x_n)_{n \in {\mathbb N}}\big) := \big\{(x, C) \in {\mathbb R} \times \mathbb{F}({\mathbb N}^+, {\mathbb N}^+) \mid(x, C) \colon \mathrm{Conv}\big((x_n)_{n \in {\mathbb N}}\big)\big\}. \end{equation*}

Similar ${\texttt{PrfMemb}}$ -sets can be defined for the set C([a, b]) of (uniformly) continuous real-valued functions on a compact interval [a, b] and for the set D([a, b]) of (uniformly) differentiable functions on a compact interval [a, b]. In this framework, the Riemann-integral is not a mapping $\int_a^b \colon C([a, b])\to {\mathbb R}$ , given by the rule $f \mapsto \int_a^b f$ . As the definition of $\int_a^b f$ depends on the modulus of continuity $\omega_f$ for f (see Bishop and Bridges 1985, pp. 51–52), the Riemman-integral is a dependent operation

The standard writing

\begin{equation*} \int_a^b f := \int_a^b(f, \omega_f) \end{equation*}

expresses the independence of the integral from the choice of a modulus of continuity, i.e.,

\begin{equation*} \int_a^b(f, \omega_f) =_{{\mathbb R}} \int_a^b(f, \omega{'}_f), \end{equation*}

for every $\omega_f, \omega{'}_f \in {\texttt{PrfMemb}}_0^{{\texttt{Cont}}(f)}$ , but it is not the accurate writing of a function from C([a, b]) to ${\mathbb R}$ , only a notational convention compatible with the classical one. The following obvious generalisation (MwE-III) of (MwE-II) to relations an a set given by an existential formula is shown similarly. A variation of (MwE-III) concerns relations on finitely many different sets.

Proposition 33. (Membership-with-Evidence III (MwE-III)) Let X, Y, Z be sets, and let S(x, y) be a relation on X of the form

\begin{equation*} S(x, y) :\Leftrightarrow \exists_{p \in Y}\big(Q(x, y, p)\big), \end{equation*}

where Q(x, y, p) is an extensional property on $X \times X \times Y$ . Let ${\texttt{PrfRel}}_0^R : X \times X\rightsquigarrow \mathbb{V}_0$ , where

\begin{equation*} {\texttt{PrfEql}}_0^S (x,y) := \{p \in Y \mid Q(x, y, p)\}, \end{equation*}

for every $x \in X$ , and let , where ${\texttt{PrfRel}}_1^S ((x,x{'})(y,y{'})) \colon {\texttt{PrfRel}}_1^S (x, x{'}) \to {\texttt{PrfRel}}_1^S (x{'}, y{'})$ is defined by the identity map-rule $\big[{\texttt{PrfRel}}_1^S( x, x{'})\big](p) := p$ , for every $p \in {\texttt{PrfRel}}_1^S (x, x{'})$ .

1. (i) The property S(x, y) is extensional.

2. (ii) The pair $\big({\texttt{PrfRel}}_0^S, {\texttt{PrfRel}}_1^S\big) \in {\texttt{Fam}}(X \times X)$ .

The “extension” of the BHK-interpretation to what usually corresponds to atomic formulas like the equality formulas is the first part of the following definition.

Definition 34 (BHK-interpretation of BISH in BST – Part I) Let membership conditions $x \in X_P$ and $x \in X_R$ as e.g., in Propositions 30 and 31, respectively. We define

\begin{equation*} {\texttt{Prf}}(x \in X_P) := {\texttt{PrfMemb}}^P_0(x), \end{equation*}

\begin{equation*} {\texttt{Prf}}(x \in X_R) := {\texttt{PrfMemb}}^R_0(x). \end{equation*}

Let a relation S(x,y) on a set X, as, e.g., in Proposition 33. We define

\begin{equation*} {\texttt{Prf}} \big(S(x,y)\big) := {\texttt{PrfRel}}_0^S(x,y).\end{equation*}

Let $\phi, \psi$ be formulas in BISH such that ${\texttt{Prf}}(\phi)$ and ${\texttt{Prf}}(\psi)$ are already defined. We define

\begin{equation*} {\texttt{Prf}}(\phi \ \& \ \psi) := {\texttt{Prf}}(\phi) \times {\texttt{Prf}}(\psi), \end{equation*}

\begin{equation*} {\texttt{Prf}}(\phi \vee \psi) := {\texttt{Prf}}(\phi) + {\texttt{Prf}}(\psi), \end{equation*}

\begin{equation*} {\texttt{Prf}}(\phi \Rightarrow \psi) := \mathbb{F}\big({\texttt{Prf}}(\phi), {\texttt{Prf}}(\psi)\big). \end{equation*}

Let $\phi(x)$ be a formula on a set X, and let ${\texttt{Prf}}^{\phi} := \big({\texttt{Prf}}^{\phi}_0,{\texttt{Prf}}^{\phi}_1\big) \in {\texttt{Fam}}(X)$ , where ${\texttt{Prf}}^{\phi}_0 \colon X \rightsquigarrow \mathbb{V}_0$ is given by the rule $x \mapsto {\texttt{Prf}}^{\phi}_0(x):= {\texttt{Prf}}\big(\phi(x)\big),$ for every $x \in X$ . The ${\texttt{Prf}}$ -sets of the formulas $\forall_{x \in X}\phi(x)$ and $\exists_{x \in X}\phi(x)$ with respect to the given family ${\texttt{Prf}}^{\phi}$ , where $\exists_{x \in X}\phi(x)$ is a formula that does not express a membership condition or a relation, are defined by

\begin{equation*} {\texttt{Prf}}\bigg(\forall_{x \in X}\phi(x)\bigg) := \prod_{x \in X}{\texttt{Prf}}^{\phi}_0(x) :=\prod_{x \in X}{\texttt{Prf}}\big(\phi(x)\big), \end{equation*}

\begin{equation*} {\texttt{Prf}}\bigg(\exists_{x \in X}\phi(x)\bigg) := \sum_{x \in X}{\texttt{Prf}}^{\phi}_0(x) :=\sum_{x \in X}{\texttt{Prf}}\big(\phi(x)\big). \end{equation*}

Due to the definition of the coproduct in Definition 13, the ${\texttt{Prf}}$ -sets for $\exists_{x \in X}\phi(x)$ and for $\forall_{x \in X}\phi(x)$ are generalizations of ${\texttt{Prf}}$ -sets for $\phi \vee \psi$ and for $\phi \ \& \ \psi$ , respectively.

Example 9.4. Let the fact: if $(x_n)_{n \in {\mathbb N}^+} \in \mathbb{F}({\mathbb N}^+, {\mathbb R})$ and $x_0 \in {\mathbb R}$ , then

\begin{equation*} x_n \stackrel{n} \longrightarrow x_0 \Rightarrow (x_n)_{n \in {\mathbb N}^+} \ \mbox{is Cauchy}. \end{equation*}

If $\chi(x_n, x_0)$ is the above implication, then $\chi(x_n, x_0)$ of the form $\phi(x_n, x_0) \Rightarrow \psi(x_n)$ . Its proof (see Bishop and Bridges 1985, p. 29) can be seen as a rule that sends a modulus of convergence $C \colon x_n \stackrel{n} \longrightarrow x_0 $ of $(x_n)_{n \in {\mathbb N}^+}$ at $x_0$ to a modulus of Cauchyness $D \colon \mathrm{Cauchy} \big((x_n)_{n \in {\mathbb N}^+}\big)$ for $(x_n)_{n \in {\mathbb N}^+}$ , where $D(k) := C(2k)$ , for every $k \in {\mathbb N}^+$ . This operation from ${\texttt{PrfMemb}}_0^{\mathrm{Conv}_{x_0}}\big((x_n)_{n \in {\mathbb N}^+}\big)$ to ${\texttt{PrfMemb}}_0^{\mathrm{Cauchy}}\big((x_n)_{n \in {\mathbb N}^+}\big)$ is a function, and

\begin{equation*} {\texttt{Prf}}(\chi(x_n, x_0)) := \mathbb{F}\bigg({\texttt{Prf}}\big(\phi(x_n, x_0)\big), {\texttt{Prf}}\big(\psi(x_n)\big)\bigg), \end{equation*}

\begin{equation*} {\texttt{Prf}}\big(\phi(x_n, x_0)\big) := {\texttt{PrfMemb}}_0^{\mathrm{Conv}_{x_0}}\big((x_n)_{n \in {\mathbb N}^+}\big), \end{equation*}

\begin{equation*} {\texttt{Prf}}\big(\psi(x_n)\big) := {\texttt{PrfMemb}}_0^{\mathrm{Cauchy}}\big((x_n)_{n \in {\mathbb N}^+}\big). \end{equation*}

Example 9.5. Let the fact: if $x_0 \in {\mathbb R}$ , then

\begin{equation*} \forall_{(x_n)_{n \in {\mathbb N}^+} \in \mathbb{F}({\mathbb N}^+, {\mathbb R})}\big( x_n \stackrel{n} \longrightarrow x_0\Rightarrow (x_n)_{n \in {\mathbb N}^+} \ \mbox{is Cauchy} \ \big). \end{equation*}

The formula corresponding to this proposition is

\begin{equation*} \chi^*(x_0) :\Leftrightarrow \forall_{x_n \in \mathbb{F}({\mathbb N}^+, {\mathbb R})}\chi(x_n, x_0), \end{equation*}

where the ${\texttt{Prf}}$ -set of $\chi(x_n, x_0) :\Leftrightarrow \big(\phi(x_n, x_0) \Rightarrow \psi(x_n)\big)$ is determined in the previous example. To determine the ${\texttt{Prf}}$ -set of $\chi^*(x_0)$ , we need to determine first a family of ${\texttt{Prf}}$ -sets over $\mathbb{F}({\mathbb N}^+, {\mathbb R})$ . Using Definition 12(ii), let

\begin{equation*} {\texttt{Prf}}^{\chi^*(x_0)} := \mathbb{F}\big({\texttt{Prf}}^{\phi(x_n, x_0)}, {\texttt{Prf}}^{\psi(x_n)}\big), \end{equation*}

and by Definition 34, we get

\begin{equation*} {\texttt{Prf}}\big(\chi^*(x_0)\big) := \prod_{x_n \in \mathbb{F}({\mathbb N}^+, {\mathbb R})}{\texttt{Prf}}\big(\chi(x_n, x_0)\big). \end{equation*}

Example 9.6. Let the fact: if $(x_n)_{n \in {\mathbb N}^+} \in \mathbb{F}({\mathbb N}^+, {\mathbb R})$ , then

\begin{equation*} (x_n)_{n \in {\mathbb N}^+} \ \mbox{is Cauchy} \Rightarrow \exists_{y \in {\mathbb R}}\big(x_n \stackrel{n} \longrightarrow y\big). \end{equation*}

The formula corresponding to this proposition is

\begin{equation*} \theta(x_n) :\Leftrightarrow \big[ \psi(x_n) \Rightarrow \exists_{y \in Y}\big(\phi(x_n, y)\big)\big]. \end{equation*}

Its proof generates a rule that associates to every $C : \mathrm{Cauchy}\big((x_n)_{n \in {\mathbb N}^+}\big)$ a pair (y, D), where $y \in {\mathbb R}$ and $D \colon x_n \stackrel{n} \longrightarrow y$ , and y is defined by the rule $y_k := \big[x_{D(k)}]_{2k},$ and $D(k) := 3k \vee C(2k)$ , for every $k \in {\mathbb N}^+$ . The use of the modulus of Cauchyness in the definition of a Cauchy sequence is responsible for the avoidance of choice in the proof. Clearly, the rule $C \mapsto (y, D)$ of the proof of $\theta(x_n)$ determines a function from ${\texttt{Prf}}(\psi(x_n))$ to the ${\texttt{Prf}}$ -set of the formula $\exists_{y \in {\mathbb R}}\phi(x_n, y)$ . Since ${\texttt{Prf}}(\phi(x_n, y)$ is already determined above, and as a corresponding family over $\mathbb{F}({\mathbb N}^+, {\mathbb R})$ is determined in Example 9.1, then, using Definition 19(iii), from Definition 34 we get

\begin{equation*} {\texttt{Prf}}(\theta(x_n)) := \sum_{y \in {\mathbb R}}{\texttt{PrfMemb}}^{\mathrm{Conv}_y}(x_n). \end{equation*}

From the last two examples, we see how the schemes of defining new families of sets from given ones can be used in order to define canonical families of ${\texttt{Prf}}$ -sets from given such families. These canonical families of ${\texttt{Prf}}$ -sets are determined in the second part of our definition of the BHK-interpretation of BISH within BST. As we have already seen in the previous two examples, the following extension of Definition 34 refers to Definitions 12 and 19.

Definition 35 (BHK-interpretation of BISH in BST – Part II) Let X, Y be sets. Let $\phi_1(x), \phi_2(x)$ be formulas in BISH such that ${\texttt{Prf}}^{\phi_1} :=\big({\texttt{Prf}}^{\phi_1}_0, {\texttt{Prf}}^{\phi_1}_1\big) \in {\texttt{Fam}}(X)$ and ${\texttt{Prf}}^{\phi_2} := \big({\texttt{Prf}}^{\phi_2}_0,{\texttt{Prf}}^{\phi_2}_1\big) \in {\texttt{Fam}}(X)$ are given. To the formulas

\begin{equation*} (\phi_1 \ \& \ \phi_2)(x) :\Leftrightarrow \phi_1(x) \ \& \ \phi_2(x), \end{equation*}

\begin{equation*} (\phi_1 \Rightarrow \phi_2)(x) :\Leftrightarrow \phi_1(x) \Rightarrow \phi_2(x), \end{equation*}

\begin{equation*} (\phi_1 \vee \phi_2)(x) :\Leftrightarrow \phi_1(x) \vee \phi_2(x), \end{equation*}

on X we associate in a canonical way the following families of sets over X, respectively:

\begin{equation*} {\texttt{Prf}}^{\phi_1 \& \phi_2} := {\texttt{Prf}}^{\phi_1} \times {\texttt{Prf}}^{\phi_2}, \end{equation*}

\begin{equation*} {\texttt{Prf}}^{\phi_1 \Rightarrow \phi_2} := \mathbb{F}\big({\texttt{Prf}}^{\phi_1}, {\texttt{Prf}}^{\phi_2}\big), \end{equation*}

\begin{equation*} {\texttt{Prf}}^{\phi_1 \vee \phi_2} := {\texttt{Prf}}^{\phi_1} + {\texttt{Prf}}^{\phi_2}. \end{equation*}

Let $\theta(x, y)$ be a formula on $X \times Y$ and ${\texttt{Prf}}^{\theta} := \big({\texttt{Prf}}^{\theta}_0, {\texttt{Prf}}^{\theta}_1\big) \in {\texttt{Fam}}(X \times Y)$ i.e., ${\texttt{Prf}}^{\theta}_0 : X \times Y \rightsquigarrow \mathbb{V}_0$ , with $(x, y) \mapsto {\texttt{Prf}}^{\theta}_0(x, y):= {\texttt{Prf}}\big(\theta(x, y)\big)$ , for every $(x, y) \in X \times Y$ . To the formulas

\begin{equation*} \big(\forall_y \theta\big)(x) :\Leftrightarrow \forall_{y \in Y}\theta(x, y), \end{equation*}

\begin{equation*} \big(\exists_y \theta\big)(x) :\Leftrightarrow \exists_{y \in Y}\theta(x, y), \end{equation*}

on X we associate in a canonical way the following families of sets over X, respectively:

\begin{equation*} {\texttt{Prf}}^{\forall_y \theta} := \prod^1 {\texttt{Prf}}^{\theta},\end{equation*}

\begin{equation*} {\texttt{Prf}}^{\exists_y \theta} := \sum^1 {\texttt{Prf}}^{\theta}.\end{equation*}

By Definitions 12 and 19, we get

\begin{equation*}{\texttt{Prf}}^{\forall_y \theta} := \bigg(\prod^1 {\texttt{Prf}}^{\theta}_0, \prod^1 {\texttt{Prf}}^{\theta}_1 \bigg),\end{equation*}

\begin{equation*} \bigg(\prod^1 {\texttt{Prf}}^{\theta}_0\bigg)(x) := \prod_{y \in Y}{\texttt{Prf}}^{\theta}_0(x, y) :=\prod_{y \in Y}{\texttt{Prf}}\big(\theta(x, y)\big), \end{equation*}

\begin{equation*} {\texttt{Prf}}^{\exists_y \theta} := \bigg(\sum^1 {\texttt{Prf}}^{\theta}_0, \sum^1 {\texttt{Prf}}^{\theta}_1 \bigg), \end{equation*}

\begin{equation*} \bigg(\sum^1 {\texttt{Prf}}^{\theta}_0\bigg)(x) := \sum_{y \in Y}{\texttt{Prf}}^{\theta}_0(x, y) :=\sum_{y \in Y}{\texttt{Prf}}\big(\theta(x, y)\big). \end{equation*}

10. Examples of Totalities with a Proof-Relevant Equality

The universe $\mathbb{V}_0$ , the powerset $\mathcal{P}(X)$ of a set X, the impredicative set ${\texttt{Fam}}(I)$ of families of sets indexed by I, the set ${\texttt{Fam}}(I, X)$ of families of subsets of X indexed by I are some of the many examples of totalities studied in Petrakis (2020c) equipped with an equality defined through an existential formula. Here we describe some more motivating examples.

10.1 The Richman ordinals

The equality on the totality of Richman ordinals, as this is defined in Mines et al. (1988, pp. 24–28), behaves similarly to the equality on the powerset. Notice that the following definition of a well-founded relation is impredicative, as it requires quantification over the powerset of a set. If $<$ is a binary relation on a set W, a subset H of W is called hereditary, if

\begin{equation*} \forall_{w \in W}\bigg(\forall_{u \in W}\big(u < w \Rightarrow u \in H\big) \Rightarrow w \in H\bigg). \end{equation*}

The relation $<$ is well-founded, if

\begin{equation*} \forall_{H \in \mathcal{P}(X)}\big(H \ \mbox{is hereditary} \ \Rightarrow H = W\big). \end{equation*}

A Richman ordinal is a pair $(\alpha, \leq)$ , where $\alpha$ is a discrete set, $\leq$ is a linear order (i.e., $x \leq y \vee y \leq x$ , for every $x, y \in \alpha$ ), and $<$ is well founded, where $x < y :\Leftrightarrow x \leq y \ \& \ x \neq_{\alpha} y$ . If $\alpha, \beta$ are ordinals, an injection $\rho : \alpha \leq \beta$ from $\alpha$ to $\beta$ is a function $\rho : \alpha \to \beta$ such that

1. (i) $\forall_{x, y \in \alpha}\big(x < y \Rightarrow \rho(x) < \rho(y)\big)$ .

2. (ii) $\forall_{z \in \beta}\forall_{y \in \alpha}\big(z < \rho(y) \Rightarrow \exists_{x \in \alpha}(\rho(x)=_{\beta} z)\big)$ .

In this case, we write $\alpha \leq \beta$ . In Mines et al. (1988, p. 28), it is shown that there is at most one injection from $\alpha$ to $\beta$ . If $\mathrm{Ord}_R$ is the totality (class) of Richman ordinals and $\alpha, \beta \in \mathrm{Ord}_R$ , we show the following.

Proposition 36. If $\rho : \alpha \leq \beta$ and $\sigma : \alpha \leq \beta$ , then $\rho$ is an embedding, and $\rho =_{\small{\mathbb{F}(\alpha, \beta)}} \sigma$ .

Proof. Let $x, y \in \alpha$ such that $\rho(x) =_{\beta} \rho(y)$ . If $x \neq_{\alpha} y$ , by the linearity of $\leq$ either $x \leq y$ or $y \leq x$ . In the first case, we get $x < y$ , hence $\rho(x) < \rho (y)$ , and in the second, we get $y < x$ , hence $\rho(y) < \rho (x)$ i.e., in both cases we get a contradiction. Hence, $x =_{\alpha} y$ . For the rest, one shows that the set $H := \{x \in \alpha \mid \rho(x) =_{\beta} \sigma (x)\}$ is hereditary (see Mines et al. 1988, p. 28).

As in the case of $\mathcal{P}(X)$ , we define $\alpha =_{\mathrm{Ord}_R} \beta :\Leftrightarrow \alpha \leq \beta \ \& \ \beta \leq \alpha$ , and

\begin{equation*}{\texttt{PrfEql}}_0(\alpha, \beta) := \{(\rho, \sigma) \in \mathbb{F}(\alpha, \beta) \times \mathbb{F}(\beta, \alpha) \mid\rho : \alpha \leq \beta\ \& \ \sigma : \beta \leq \alpha\}.\end{equation*}

Since the composition of injections is an injection, let

\begin{equation*}{\texttt{refl}}(\alpha) := \big(\mathrm{id}_{\alpha}, \mathrm{id}_{\alpha}\big) \ \ \& \ \ (\rho, \sigma)^{-1} := (\sigma, \rho)\ \ \& \ \ (\rho, \sigma) \ast (\tau, v) := (\tau \circ \rho, \sigma \circ v),\end{equation*}

and the groupoid properties for ${\texttt{PrfEql}}_0(\alpha, \beta)$ hold trivially by the equality of all its elements.

10.2 The direct sum of a direct family of sets

Next we define the

Definition 37. Let $(I, \preccurlyeq_I)$ be a directed set, and $D^{\preccurlyeq}(I) := \big\{(i, j) \in I \times I \mid i \preccurlyeq_I j \big\}$ the diagonal of $\preccurlyeq_I$ . A direct family of sets $(I, \preccurlyeq_I)$ , or an $(I, \preccurlyeq_I)$ -family of sets, is a pair $\Lambda^{\preccurlyeq} := (\lambda_0, \lambda_1^{\preccurlyeq})$ , where $\lambda_0 : I \rightsquigarrow \mathbb{V}_0$ , and $\lambda_1^{\preccurlyeq}$ , a modulus of transport maps for $\lambda_0$ , is defined by

such that the transport maps $\lambda_{ij}^{\prec}$ of $\Lambda^{\preccurlyeq}$ satisfy the following conditions:

1. (a) For every $i \in I$ , we have that $\lambda_{ii}^{\preccurlyeq} := \mathrm{id}_{\lambda_0(i)}$ .

2. (b) If $i \preccurlyeq_I j$ and $j \preccurlyeq_I k$ , the following diagram commutes

If $X \in \mathbb{V}_0$ , the constant $(I, \preccurlyeq_I)$ -family X is the pair $C^{\preccurlyeq,X} := (\lambda_0^X, \lambda_1^{\preccurlyeq,X})$ , where $\lambda_0^X (i) := X$ , and $\lambda_1^{\preccurlyeq,X} (i, j) := \mathrm{id}_X$ , for every $i \in I$ and $(i, j) \in D^{\preccurlyeq}(I)$ .

Since in general $\preccurlyeq_I$ is not symmetric, the transport map $\lambda_{ij}^{\preccurlyeq}$ does not necessarily have an inverse. Hence, $\lambda_1^{\preccurlyeq}$ is only a modulus of transport for $\lambda_0$ , in the sense that it determines the transport maps of $\Lambda^{\preccurlyeq}$ , and not necessarily a modulus of function-likeness for $\lambda_0$ .

Definition 38. If $\Lambda^{\preccurlyeq} := (\lambda_0, \lambda_1^{\preccurlyeq})$ and $M^{\preccurlyeq}:= (\mu_0, \mu_1^{\preccurlyeq})$ are $(I, \preccurlyeq_I)$ -families of sets, a direct family-map $\Phi$ from $\Lambda^{\preccurlyeq}$ to $M^{\preccurlyeq}$ , denoted by $\Phi \colon \Lambda^{\preccurlyeq} \Rightarrow M^{\preccurlyeq}$ , their set ${\texttt{Map}}_{(I, \preccurlyeq_I)}(\Lambda^{\preccurlyeq}, M^{\preccurlyeq})$ , and the totality ${\texttt{Fam}}(I, \preccurlyeq_I)$ of $(I, \preccurlyeq_I)$ -families are defined in the expected way. The direct sum $\sum_{i \in I}^{\preccurlyeq}\lambda_0(i)$ over $\Lambda^{\preccurlyeq}$ is the totality $\sum_{i \in I}\lambda_0(i)$ equipped with the equality

\begin{equation*} (i, x) =_{\sum_{i \in I}^{\preccurlyeq} \lambda_0(i)} (j, y) : \Leftrightarrow \exists_{k \in I}\big(i \preccurlyeq_I k \ \& \ j \preccurlyeq_I k \ \& \ \lambda_{ik}^{\preccurlyeq}(x) =_{\lambda_0(k)} \lambda_{jk}^{\preccurlyeq}(y)\big). \end{equation*}

The totality $\prod_{i \in I}^{\preccurlyeq}\lambda_0(i)$ of dependent functions over $\Lambda^{\preccurlyeq}$ is defined by

\begin{equation*} \Phi \in \prod_{i \in I}^{\preccurlyeq}\lambda_0(i) :\Leftrightarrow \Phi \in \mathbb{A}(I, \lambda_0)\ \& \ \forall_{(i,j) \in D^{\preccurlyeq}(I)}\big(\Phi_j =_{\lambda_0(j)} \lambda_{ij}^{\preccurlyeq}(\Phi_i)\big), \end{equation*}

and it is equipped with the equality of $\mathbb{A}(I, \lambda_0)$ .

If $\Lambda^{\preccurlyeq} := \big(\lambda_0, \lambda_1^{\preccurlyeq}\big) \in {\texttt{Fam}}(I, \preccurlyeq_I)$ , and if $i, x), (j, y) \in\sum_{i \in I}^{\preccurlyeq} \lambda_0(i)$ , and since by Definition 38

\begin{equation*} (i, x) =_{\sum_{i \in I}^{\preccurlyeq} \lambda_0(i)} (j, y) : \Leftrightarrow \exists_{k \in I}\big(i \preccurlyeq_I k \ \& \ j \preccurlyeq_I k \ \& \ \lambda_{ik}^{\preccurlyeq}(x) =_{\lambda_0(k)} \lambda_{jk}^{\preccurlyeq}(y)\big), \end{equation*}

let

\begin{equation*} {\texttt{PrfEql}}_0\big((i, x), (j, y)\big) := \big\{m \in I_{ij} \mid \lambda_{im}^{\preccurlyeq}(x) =_{\lambda_0(m)}\lambda_{jm}^{\preccurlyeq}(y)\big\}, \end{equation*}

\begin{equation*} I_{ij} := \{k \in I \mid i \preccurlyeq_I k \ \& \ j \preccurlyeq_I k\}.\end{equation*}

To show the extensionality of ${\texttt{PrfEql}}_0\big((i, x), (j, y)\big)$ , let $m{'} =_{ I_{ij}} m :\Leftrightarrow m{'} =_I m$ and $\lambda_{im}^{\preccurlyeq}(x) =_{\lambda_0(m)} \lambda_{jm}^{\preccurlyeq}(y)$ . As $\preccurlyeq_I$ is extensional and reflexive, $m \preccurlyeq_I m{'}$ , and by Definition 37(b) $\lambda_{im{'}}^{\preccurlyeq}(x) = \lambda_{mm{'}}^{\preccurlyeq}\big(\lambda_{im}^{\preccurlyeq}(x)\big) =\lambda_{mm{'}}^{\preccurlyeq}\big(\lambda_{jm}^{\preccurlyeq}(y)\big) = \lambda_{jm{'}}^{\preccurlyeq}(y)$ . To define an operation of composition, we work with directed sets equipped with a modulus of directedness $\delta$ . In the case of a partial order like the standard relation $\leq$ on ${\mathbb R}$ , the functions $\delta(x, y) := x \vee y := \max\{x, y\}$ is such a modulus.

Definition 39. Let $(I, \preccurlyeq_I)$ be a poset, i.e., a preorder such that $\big[i \preccurlyeq_I j \ \& \ j \preccurlyeq_I i \big]\Rightarrow i =_I j$ , for every $i, j, \in I$ . A modulus of directedness for I is a function $\delta \colon I \times I \to I$ , such that for every $i, j, k \in I$ the following conditions are satisfied:

$(\delta_1)$ $i \preccurlyeq_I \delta(i, j)$ and $j \preccurlyeq_I \delta(i, j)$ .

$(\delta_2)$ If $i \preccurlyeq_I j$ , then $\delta(i, j) =_I \delta(j, i) =_I j$ .

$(\delta_3)$ $\delta\big(\delta(i, j), k\big) =_I \delta\big(i, \delta(j, k)\big)$ .

Proposition 40. Let $\delta$ be a modulus of directedness on a poset $(I, \preccurlyeq_I)$ , and let $\Lambda^{\preccurlyeq}:= (\lambda_0, \lambda_1^{\preccurlyeq})$ be a family of sets over $(I, \preccurlyeq_I)$ .

1. (i) $\delta(i, i) =_I i$ , for every $i \in I$ .

2. (ii) $\delta(i, j) =_I \delta(j, i)$ , for every $i, j \in I$ .

3. (iii) If $(i, x) =_{\sum_{i \in I}^{\preccurlyeq} \lambda_0(i)} (j, y) =_{\sum_{i \in I}^{\preccurlyeq}\lambda_0(i)} (k, z)$ , then

   \begin{equation*} m \in {\texttt{PrfEql}}_0\big((i, x), (j, y)\big) \ \& \ l \in {\texttt{PrfEql}}_0\big((j, y), (k, z)\big) \ \Rightarrow \ \delta(m, l)\in {\texttt{PrfEql}}_0\big((i, x), (k, z)\big). \end{equation*}

Proof.

1. (i) Since $i \preccurlyeq_I i$ , we use the definitional clause ( $\delta_1$ ) of a modulus of directedness.

2. (ii) By ( $\delta_3$ ) we have that $\delta\big(\delta(i, j), i\big) =_I \delta\big(i, \delta(j, i)\big)$ . By ( $\delta_1$ ) and ( $\delta_2$ ), we get $\delta\big(\delta(i, j), i\big) =_I \delta(i, j)$ and $\delta\big(i, \delta(j, i)\big) =_I \delta(j, i)$ .

3. (iii) If $m \in {\texttt{PrfEql}}_0\big((i, x), (j, y)\big) \Leftrightarrow m \in I_{ij} \ \& \ \lambda_{im}^{\preccurlyeq}(x) =_{\lambda_0(m)}\lambda_{jm}^{\preccurlyeq}(y)$ , and $l \in {\texttt{PrfEql}}_0\big((j, y), (k, z)\big) \Leftrightarrow l \in I_{jk} \ \& \ \lambda_{jl}^{\preccurlyeq}(y)=_{\lambda_0(l)} \lambda_{kl}^{\preccurlyeq}(z)$ , we show that $\delta(m, l) \in I_{ik}$ and $\lambda_{i\delta(m,l)}^{\preccurlyeq}(x) =_{\lambda_0(\delta(m, l)} \lambda_{k \delta(m, l)}^{\preccurlyeq}(z)$ . By our hypotheses, $i \preccurlyeq_I m \preccurlyeq_I \delta(m, l)$ and $k \preccurlyeq_I l \preccurlyeq_I \delta(m, l)$ . Moreover,

   \begin{gathered} \lambda _{i\delta (m,l)}^ \preccurlyeq (x){\text{ }}\;\mathop = \limits^{i{ \preccurlyeq _I}m{ \preccurlyeq _I}\delta (m,l)} \;\;\;\lambda _{m\delta (m,l)}^ \preccurlyeq (\lambda _{im}^ \preccurlyeq (x)) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{}} = \;\;\;\;\;\;\;\;\;\;\lambda _{m\delta (m,l)}^ \preccurlyeq (\lambda _{jm}^ \preccurlyeq (y))\; \hfill \\\;\;\;\;\;\;{\text{ }}\;\;\mathop = \limits^{j{ \preccurlyeq _I}m{ \preccurlyeq _I}\delta (m,l)} \;\;\;\;\;\lambda _{j\delta (m,l)}^ \preccurlyeq (y) \hfill \\\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{ }}\mathop = \limits^{j{ \preccurlyeq _I}l{ \preccurlyeq _I}\delta (m,l)} \;\;\;\;\lambda _{l\delta (m,l)}^ \preccurlyeq (\lambda _{jl}^ \preccurlyeq (y)) \hfill \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{ }}\;\;\; = \;\;\;\;\;\;\;\;\;\;\lambda _{l\delta (m,l)}^ \preccurlyeq (\lambda _{kl}^ \preccurlyeq (z)) \hfill \\ \;\;\;\;\;{\text{ }}\;\mathop = \limits^{k{ \preccurlyeq _I}l{ \preccurlyeq _I}\delta (m,l)} \;\;\;\;\lambda _{k\delta (m,l)}^ \preccurlyeq (z). \hfill \\ \end{gathered}

If $m \in {\texttt{PrfEql}}_0\big((i, x), (j, y)\big)$ and $l \in {\texttt{PrfEql}}_0\big((j, y), (k, z)\big)$ , it is natural to define

\begin{equation*}{\texttt{refl}}(i, x) := i \ \ \& \ \ m^{-1} := m \ \ \& \ \ m \ast l := \delta(m, l).\end{equation*}

Then, ${\texttt{refl}}(i, x) \ast m := i \ast m := \delta(i, m) =_I m$ , and similarly $m \ast {\texttt{refl}}(i, x) =_I m$ , for every $m \in {\texttt{PrfEql}}_0\big((i, x), (j, y)\big)$ . The associativity $(m \ast l) \ast n =_I m \ast (l \ast n)$ is just the condition ( $\delta_3$ ), and if $m, m{'} \in {\texttt{PrfEql}}_0\big((i, x), (j, y)\big)$ and $l \in {\texttt{PrfEql}}_0\big((j, y), (k, z)\big)$ such that $m =_I m{'}$ and $l =_I l{'}$ , then $m \ast l =_I m{'} \ast l{'}$ is reduced to $\delta(m, l) = \delta(m{'}, l{'})$ , which follows from the fact that $\delta$ is a function. If $m \in {\texttt{PrfEql}}_0\big((i, x), (j, y)\big)$ , to show $m \ast m^{-1} = {\texttt{refl}}(i, x) := i$ , we need to use as equality on ${\texttt{PrfEql}}_0\big((i, x), (i, x)\big)$ not the equality inherited from I, but the equality

\begin{equation*} m =_{{\texttt{PrfEql}}_0\big((i, x), (i, x)\big)} m{'} :\Leftrightarrow i =_I i, \end{equation*}

according to which all elements of ${\texttt{PrfEql}}_0\big((i, x), (i, x)\big)$ are equal to each other. Similarly, we get $m^{-1} \ast m := \delta(m^{-1}, m) =_{{\texttt{PrfEql}}_0\big((i, x), (i, x)\big)} j := {\texttt{refl}}(j, y)$ . Hence, the equality on ${\texttt{PrfEql}}_0\big((i, x), (j, y)\big)$ is defined as above, if $i := j$ and $x := y$ , and it is inherited from I otherwise. In order to make such a distinction though, we need to know that the previous equalities are possible, something which is not always the case without some further assumptions on the general equality $:=$ . Of course, all aforementioned groupoid properties of $\ast$ and -1 hold, if we define all elements of any set ${\texttt{PrfEql}}_0\big((i, x), (j, y)\big)$ to be equal.

10.3 The set of reals

In Bishop and Bridges (1985, p. 18), the set of reals ${\mathbb R}$ is defined as an extensional subset of $\mathbb{F}({\mathbb N}^+, \mathbb{Q})$ . Specifically,

\begin{equation*} {\mathbb R} := \bigg\{x \in \mathbb{F}({\mathbb N}^+, \mathbb{Q}) \mid \forall_{m, n \in {\mathbb N}^+}\bigg(|x_m - x_n| \leq \frac{1}{m} +\frac{1}{n}\bigg)\bigg\}, \end{equation*}

where ${\mathbb N}^+$ is the set of non-zero natural numbers. The equality on ${\mathbb R}$ is defined as follows:

\begin{equation*} x =_{{\mathbb R}} y :\Leftrightarrow \forall_{n \in {\mathbb N}^+}\bigg(|x_n - y_n| \leq \frac{2}{n}\bigg). \end{equation*}

To prove though that $x =_{{\mathbb R}} y$ is transitive, one needs the following characterization:

\begin{equation*} x =_{{\mathbb R}} y \Leftrightarrow \forall_{j \in {\mathbb N}^+}\exists_{N_j \in {\mathbb N}^+}\forall_{n \geq N_j}\bigg(|x_n - y_n|\leq\frac{1}{j}\bigg). \end{equation*}

Using countable choice, we get the equivalence

\begin{equation*} x =_{{\mathbb R}} y \Leftrightarrow \exists_{\omega \in \mathbb{F}({\mathbb N}^+, {\mathbb N}^+)}\forall_{j\in {\mathbb N}^+}\forall_{n \geq \omega(j)}\bigg(|x_n - y_n| \leq \frac{1}{j}\bigg).\end{equation*}

If $\omega : {\mathbb N}^+ \to {\mathbb N}^+$ witnesses the equality $x =_{{\mathbb R}} y$ , then $\omega \vee \mathrm{id}_{{\mathbb N}^+}$ , where $(\omega \vee \mathrm{id}_{{\mathbb N}^+})(j) := \omega (j) \vee \mathrm{id}_{{\mathbb N}^+} (j) :=\max \{\omega (j), \mathrm{id}_{{\mathbb N}^+}(j)\}$ , for every $j \in {\mathbb N}^+$ , also witnesses the equality $x =_{{\mathbb R}} y$ . Hence, without loss of generality, we can assume that $\omega \geq \mathrm{id}_{{\mathbb N}^+}$ . We define

\begin{equation*} {\texttt{PrfEql}}_0(x, y) := \big\{\omega \in \mathbb{F}({\mathbb N}^+, {\mathbb N}^+) \mid \omega : x =_{{\mathbb R}} y\big\},\end{equation*}

\begin{equation*}\omega : x =_{{\mathbb R}} y :\Leftrightarrow \omega \geq \mathrm{id}_{{\mathbb N}^+} \ \& \ \forall_{j \in {\mathbb N}^+}\forall_{n \geq \omega(j)}\bigg(|x_n - y_n| \leq \frac{1}{j}\bigg).\end{equation*}

If $\omega \in {\texttt{PrfEql}}_0(x, y)$ and $\delta \in {\texttt{PrfEql}}_0(y, z)$ , we define

\begin{equation*} {\texttt{refl}}(x) := \mathrm{id}_{{\mathbb N}^+} \ \ \& \ \ \omega^{-1} := \omega \ \ \& \ \ (\omega \ast \delta)(j) :=\omega (2j) \vee \delta (2j),\end{equation*}

for every $j \in {\mathbb N}^+$ . In this case, $\omega \ast \delta \in {\texttt{PrfEql}}_0(x, z)$ , since if $n \geq\omega (2j) \vee \delta (2j)$ , then

\begin{equation*} |x_n - z_n| \leq |x_n - y_n| + |y_n - z_n| \leq \frac{1}{2j} + \frac{1}{2j} = \frac{1}{j}.\end{equation*}

It is easy to see that $\ast$ is associative, and it also compatible with the canonical equality of the sets ${\texttt{PrfEql}}_0(x, y)$ , the one inherited from $\mathbb{F}({\mathbb N}^+, {\mathbb N}^+)$ . The rest of the groupoid properties of $\ast$ and -1 do not hold if we keep the canonical equality of the sets ${\texttt{PrfEql}}_0(x, y)$ . In other words, the set ${\texttt{PrfEql}}_0^{{\mathbb R}}(x, y)$ , equipped with its canonical equality, is not a $(-1)$ -set. It becomes, if we truncate it, i.e., if we equip ${\texttt{PrfEql}}_0^{{\mathbb R}}(x, y)$ with the equality

\begin{equation*} \omega \ \small{\small{\small{\lvert \lvert =_{\mathbb{F}({\mathbb N}^+, {\mathbb N}^+)} \rvert \rvert}}}\ \delta :\Leftrightarrow \omega =_{\mathbb{F}({\mathbb N}^+, {\mathbb N}^+)} \omega \ \ \& \ \ \delta =_{\mathbb{F}({\mathbb N}^+, {\mathbb N}^+)} \delta. \end{equation*}

If (X, d) is a metric space, hence $x =_X y \Leftrightarrow d(x, y) = 0$ , for every $x, y \in X$ , we define

\begin{equation*} {\texttt{PrfEql}}_0(x, y) := {\texttt{PrfEql}}_0\big(d(x, y), 0\big).\end{equation*}

If F is a set of real-valued functions on a set X, like a Bishop topology on X (see Petrakis 2015a), that separates the points of X i.e., $ x =_X y \Leftrightarrow \forall_{f \in F}\big(f(x) =_{{\mathbb R}} f(y)\big),$ we define

If $\phi : {\mathbb R} \to {\mathbb R}$ , let a dependent operation

For example, let $[\phi_1(x, y, \omega)](j) := 2j$ , for every $j \in {\mathbb N}^+$ . This element of ${\texttt{PrfEql}}_0\big(f(x), f(y)\big)$ though does not depend on $\omega$ , and it is not compatible with $\ast$ and ^–1.

10.4 Sets of integrable and measurable functions in Bishop–Cheng measure theory

In Bishop–Cheng measure theory $(\mathrm{BCMT})$ , Bishop and Cheng define the set of integrable functions of an integration space $\mathcal{L} := (X, L, \int)$ (see Bishop and Bridges 1985, p. 222) as the totality

\begin{equation*} L_1 := \{f \in \mathfrak{F}(X) \mid f \ \mbox{has a representation in} \ L\},\end{equation*}

where $\mathfrak{F}(X)$ is the totality of real-valued partial functions on the set X, which are strongly extensional, i.e., if $f(x) \neq_{{\mathbb R}} f(x{'})$ , then $x \neq_X x{'}$ , for every $x, x{'} \in X$ . An element f of $\mathfrak{F}(X)$ has a representation in L, if there is a sequence $(f_n)_{n = 1}^{\infty}$ of partial functions in L such that

\begin{equation*} \sum_{n \in {\mathbb N}^+}\int|f_n| < + \infty, \ \ \ \ \mbox{and} \end{equation*}

\begin{equation*} \forall_{x \in X}\bigg(\sum_{n \in {\mathbb N}^+}|f_n(x)| < + \infty \Rightarrow f(x) = \sum_{n \in {\mathbb N}^+}f_n(x)\bigg). \end{equation*}

A subset F of X is full, if there is $g \in L_1$ such that the domain of (the partial function) g is included in F. The equality on $L_1$ is defined in Bishop and Bridges (1985, p. 224) by

\begin{equation*} f =_{L_1} g :\Leftrightarrow \exists_{F \in \mathcal{P}(X)}\big(F \ \mbox{is full} \ \& \ f_{|F} = g_{|F}\big).\end{equation*}

Unfortunately, this presentation of $L_1$ within BCMT is highly problematic from a predicative point of view. The totality $L_1$ is defined through separation on $\mathfrak{F}(X)$ , which, because of the definition of a partial function from X to ${\mathbb R}$ , is a class, like $\mathcal{P} (X)$ , and not a set (see Petrakis 2020 c, Section 7.4). Moreover, the above equality $f =_{L_1} g$ requires quantification over the class $\mathcal{P}(X)$ . The impredicative character of BCMT hinders its computational content (see Petrakis 2020 c Chapter 7, Zeuner 2019, and Petrakis and Zeuner 2022). Within this impredicative theory BCMT though, one can define

\begin{equation*} {\texttt{PrfEql}}_0(f, g) := \{F \in \mathcal{P}(X) \mid F \ \mbox{is full} \ \& \ f_{|F} = g_{|F}\}.\end{equation*}

If $f, g, h \in L_1$ , $F \in {\texttt{PrfEql}}_0(f, g)$ , and $G \in {\texttt{PrfEql}}_0(g, h)$ , it is natural to define

\begin{equation*} {\texttt{refl}}(f) := \mathrm{dom}(f) \ \ \& \ \ F^{-1} := F \ \ \& \ \ F \ast G := F \cap G,\end{equation*}

since the intersection of full sets is a full set, and $f_{|F} = g_{|F} \ \& \ g_{|G} = h_{|G} \Rightarrow f_{|F \cap G} = h_{|F \cap G}$ . It is not hard to see that if we equip the sets ${\texttt{PrfEql}}_0(f, g)$ with the equality inherited from $\mathcal{P}(X)$ , we get the same groupoid properties of $\ast$ and -1 as in the case of ${\mathbb R}$ in the previous example. If $\int$ is a completely extended (see Bishop and Bridges 1985, p. 223), and $\sigma$ -finite integral on X (see Bishop and Bridges 1985, p. 269), and if $p \geq 1$ , the set $L_p$ is defined as follows (see Bishop and Bridges 1985, p. 315):

\begin{equation*} L_1 := \{f \in \mathfrak{F}(X) \mid f \ \mbox{is measurable} \ \& \ |f|^p \in L_1\},\end{equation*}

where a partial function $f : X \rightharpoonup {\mathbb R}$ is measurable, if its domain $\mathrm{dom}(f)$ is a full set, and it is appropriately approximated by elements of $L_1$ (for the exact definition see Bishop and Bridges 1985, p. 259). Similarly to $L_1$ , $ f =_{L_p} g :\Leftrightarrow \exists_{F \in \mathcal{P}(X)}\big(F \ \mbox{is full} \ \& \ f_{|F} = g_{|F}\big)$ . If $\int$ is a $\sigma$ -finite integral on X, the set $L_{\infty}$ is defined as follows (see Bishop and Bridges 1985, p. 346):

\begin{equation*} L_{\infty} := \big\{f \in \mathfrak{F}(X) \mid f \ \mbox{is measurable and essentially bounded relative to}\ \mbox{$\int$} \big\},\end{equation*}

where a real-valued function defined on a full subset of X is essentially bounded relative to a $\sigma$ -finite integral $\int$ on X, if there are $c > 0$ and a full set F, such that $|f|_{|F} \leq c$ (see Bishop and Bridges 1985, p. 346). The equality on $L_{\infty}$ is defined as in $L_p$ , for $p \geq 1$ , and the corresponding sets ${\texttt{PrfEql}}_0(f, g)$ behave analogously. A complemented subset $\boldsymbol A := (A^1, A^0)$ of X (see Petrakis 2020 c, Section 2.8) is called integrable, if its characteristic function $\chi_{\boldsymbol A}$ is in $L_1$ , and then the measure on $\boldsymbol A$ is defined by $ \mu (\boldsymbol A) := \int \chi_{\boldsymbol A}$ . If $\mathcal{A}$ is the totality of integrable sets with positive measure, $=_{\mathcal{A}}$ is defined in Bishop and Bridges (1985), p. 346, by $\boldsymbol A =_{\mathcal{A}} \boldsymbol B :\Leftrightarrow \chi_{\boldsymbol A} =_{L_1} \chi_{\boldsymbol B}$ , and one can define ${\texttt{PrfEql}}_0(\boldsymbol A, \boldsymbol B) :={\texttt{PrfEql}}_0(\chi_{\boldsymbol A}, \chi_{\boldsymbol B})$ . All these totalities though are defined impredicatively.

11. Martin-Löf Sets

We give an abstract description of the previous examples of totalities (sets) with a proof-relevant equality. The introduced Martin-Löf sets give us the opportunity to transfer results and concepts from MLTT or HoTT into BST. So far, only the transition of results and concepts from BISH to MLTT was considered. This aspect of Martin-Löf sets is one of the major reasons behind their study in this paper

Definition 41. Let Y be a set, and $(X, =_X)$ a set with an equality condition of the form

\begin{equation*} x =_X x{'} :\Leftrightarrow \exists_{p \in Y}\big(p: x =_X x{'}\big), \end{equation*}

where $\theta^{x x{'}}(p) :\Leftrightarrow p: x =_X x{'}$ is an extensional property on Y. Let also the nondependent assignment routine ${\texttt{PrfEql}}_0^X \colon X \times X \rightsquigarrow \mathbb{V}_0$ defined by

\begin{equation*} {\texttt{PrfEql}}_0^X(x, x{'}) := \{p \in Y \mid p : x =_X x{'}\}; \ \ \ \ (x, x{'}) \in X \times X,\end{equation*}

together with dependent operations

We call the structure $\widehat{X} := (X, =_X, {\texttt{PrfEql}}_0^X, {\texttt{refl}}^X, ^{-1_X}, \ast_X)$ a set with a proof-relevant equality. If X is clear from the context, we may omit the subscript X from the above dependent operations. We call $\widehat{X}$ a Martin-Löf set, if the following conditions hold:

$(\mathrm{ML}_1)$ ${\texttt{refl}}_x \ast p =_{{\texttt{PrfEql}}_0^X(x, x{'})} p$ and $p \ast {\texttt{refl}}_y =_{{\texttt{PrfEql}}_0^X(x, x{'})} p$ , for every $p \in{\texttt{PrfEql}}_0^X(x, x{'})$ .

$(\mathrm{ML}_2)$ $p \ast p^{-1} =_{{\texttt{PrfEql}}_0^X(x, x)} {\texttt{refl}}_x$ and $p^{-1} \ast p =_{{\texttt{PrfEql}}_0^X(y, y)} {\texttt{refl}}_y$ , for every $p \in {\texttt{PrfEql}}_0^X(x, x{'})$ .

$(\mathrm{ML}_3)$ $(p \ast q) \ast r =_{{\texttt{PrfEql}}_0^X(x, x{'''})} p \ast ( q \ast r)$ , for every $p \in {\texttt{PrfEql}}_0^X(x, x{'}),q \in {\texttt{PrfEql}}_0^X(x{'}, x{''})$ and $r \in {\texttt{PrfEql}}_0^X(x{''}, x{'''})$ .

$(\mathrm{ML}_4)$ If $p, q \in {\texttt{PrfEql}}_0^X(x, x{'})$ and $r, s \in {\texttt{PrfEql}}_0^X(x{'}, x{''})$ such that $p=_{{\texttt{PrfEql}}_0^X(x, x{'})} q$ and $r =_{{\texttt{PrfEql}}_0^X(x{'}, x{''})} s$ , then $p \ast r =_{{\texttt{PrfEql}}_0^X(x, x{''})} q \ast s$ .

If $\widehat{X}$ is a set with a proof-relevant equality, by Definition 34, we get

\begin{equation*} {\texttt{Prf}}(x =_X x{'}) := {\texttt{PrfEql}}_0^X(x, x{'}).\end{equation*}

Conditions $(\mathrm{ML}_1)-(\mathrm{ML}_3)$ express that the proof-relevant equality of X has a groupoid-structure, see Palmgren (2012a), while condition $(\mathrm{ML}_4)$ expresses the extensionality of the composition ^*X.

Example 11.1. A nontrivial example of a Martin-Löf set is ${\texttt{Fam}}(I, X)$ the set of families of subsets of the set X indexed by the set I (see Definition 23), while the proof that ${\texttt{Fam}}(I, X)$ satisfies properties $(\mathrm{ML}_1)-(\mathrm{ML}_4)$ follows from Definition 27. Similarly, one can show that ${\texttt{Fam}}(I, \mathbf{X})$ , the set of families of complemented subsets of the set X indexed by the set I (see Section 4.9 in Petrakis 2020 c) and ${\texttt{Fam}}(I, X, Y)$ , the set of families of partial functions ⁴ from the set X to the set Y indexed by the set I (see Section 4.8 in Petrakis 2020 c) are Martin-Löf sets. We get trivial examples of Martin-Löf sets by using the truncation of a set (see also our remark in Subsection 10.3 on getting the groupoid properties of the proof sets of reals by truncating them).

Next proposition is straightforward to show.

Proposition 42. Let $\widehat{X}$ be a Martin-Löf set, $x, x{'} \in X$ , and $p, q \in {\texttt{PrfEql}}_0(x, x{'})$ .

1. (i) ${\texttt{refl}}_x^{-1} =_{{\texttt{PrfEql}}_0(x, x)} {\texttt{refl}}_x$ .

2. (ii) $(p^{-1})^{-1} =_{{\texttt{PrfEql}}_0(x, x{'})} p$ .

3. (iii) If $p =_{{\texttt{PrfEql}}_0(x, x{'})} q$ , then $p^{-1} =_{{\texttt{PrfEql}}_0(x{'}, x)} q^{-1}$ .

Definition 43. Let $\widehat{X}, \widehat{Y}$ be sets with proof-relevant equalities. A map from $\widehat{X}$ to $\widehat{Y}$ is a pair $\widehat{f} := (f, f_1)$ , where $f \colon X \to Y$ and

We write $\widehat{f} \colon \widehat{X} \to \widehat{Y}$ to denote a map from $\widehat{X}$ to $\widehat{Y}$ . We call the dependent operation $f_1$ the first associate of $\widehat{f}$ . If, for every $x, x{'} \in X$ and every $p, p{'} \in {\texttt{PrfEql}}_0^X(x, x{'})$ , we have that

\begin{equation*} p =_{{\texttt{PrfEql}}_0^X(x, x{'})} p{'} \Rightarrow f_1(x, x{'}, p) =_{{\texttt{PrfEql}}_0^Y(f(x), f(x{'}))} f_1(x, x{'}, p{'}), \end{equation*}

we say that $f_1$ is a function-like first associate of $\widehat{f}$ . If $\widehat{X}$ and $\widehat{Y}$ are Martin-Löf sets, a map $\widehat{f} \colon \widehat{X} \to \widehat{Y}$ is a Martin-Löf map, if the following conditions hold:

1. (i) $f_1(x, x, {\texttt{refl}}_x) =_{{\texttt{PrfEql}}_0^Y(f(x), f(x))} {\texttt{refl}}_{f(x)}$ , for every $x \in X$ .

2. (ii) If $x =_X x{'} =_X x{''}$ , then $f_1(x, x{''}, p \ast q) =_{{\texttt{PrfEql}}_0^Y(f(x), f(x{''}))}f_1(x, x{'}, p)\ast f_1(x{'}, x{''}, q)$ , for every $p \in {\texttt{PrfEql}}_0^X(x, x{'})$ and $q \in {\texttt{PrfEql}}_0^X(x{'}, x{''})$ .

Definition 44. 1Let $\widehat{I}$ be a set with a proof-relevant equality. A family of sets over $\widehat{I}$ is a triplet $\widehat{\Lambda} := (\lambda_0, {\texttt{PrfEql}}_0^I, \lambda_2)$ , where $\lambda_0 : I \rightsquigarrow \mathbb{V}_0$ , and

such that the following conditions hold:

1. (i) For every $i \in I$ , we have that $\lambda_{ii}^{{\texttt{refl}}_i} = \mathrm{id}_{\lambda_0(i)}$ .

2. (ii) If $i =_I j =_I k$ , for every $p \in {\texttt{PrfEql}}_0^I(i, j)$ and $q \in {\texttt{PrfEql}}_0^I(j, k)$ , the following diagram commutes

1. (iii) If $i =_I j$ , then for for every $p \in {\texttt{PrfEql}}_0^I(i, j)$ , the following diagrams commute

A family-map $\Phi \colon \widehat{\Lambda} \Rightarrow \widehat{M}$ is defined as in Definition 21. We denote by ${\texttt{Fam}}(\widehat{I})$ the totality of families of sets over $\widehat{I}$ , which is equipped with the obvious equality. We call $\widehat{\Lambda}$ proof-irrelevant, if for every $(i, j) \in D(I)$ and $p, p{'} \in {\texttt{PrfEql}}_0^I(i, j)$ , we have that $\lambda_{ij}^p =_{\mathbb{F}(\lambda_0(i), \lambda_0(j))} \lambda_{ij}^{p{'}}$ .

If $\widehat{\Lambda} \in {\texttt{Fam}}(\widehat{I})$ , then $\widehat{\Lambda} \in {\texttt{Fam}}^*(I)$ (see Definition 20). If $\widehat{\Lambda}$ is function-like family over $\widehat{I}$ , condition (iii) of the previous definition is provable, while if $\widehat{\Lambda}$ is proof-irrelevant, then $\widehat{\Lambda}$ is function-like. Following Definition 22, we denote the $\sum$ -set of $\widehat{\Lambda}$ by $\widehat{\sum}_{i \in I}\lambda_0(i)$ , where

\begin{equation*} (i, x) =_{\widehat{\sum}_{i \in I} \lambda_0 (i)} (j, y) : \Leftrightarrow i =_I j \ \& \ \exists_{p \in {\texttt{PrfEql}}_0^I(i, j)}\big(\lambda_{ij}^p (x) =_{\lambda_0 (j)} y\big),\end{equation*}

and we denote the $\prod$ -set of $\widehat{\Lambda}$ , equipped with the pointwise equality, by $\widehat{\prod}_{i\in I}\lambda_0(i)$ , where

\begin{equation*} \Theta \in \widehat{\prod}_{i \in I}\lambda_0(i) :\Leftrightarrow \Theta \in \mathbb{A}(I, \lambda_0) \ \&\ \forall_{p \in {\texttt{PrfEql}}_0^I(i,j)}\big(\Theta_j =_{\lambda_0(j)} \lambda_{ij}^p(\Theta_i)\big). \end{equation*}

Proposition 45. If $\widehat{\Lambda} := (\lambda_0, {\texttt{PrfEql}}_0^I, \lambda_2)$ is a function-like family of sets over the Martin-Löf set $\widehat{I}$ , then a structure of a Martin-Löf set is defined on $\widehat{\sum}_{i \in I} \lambda_0 (i)$ .

Proof. Since $\widehat{\Lambda}$ is function-like, the property $Q_{ij}^{xy}(p) :\Leftrightarrow \lambda_{ij}^p(x)= y$ is extensional on the set ${\texttt{PrfEql}}_0^I(i, j)$ , and we can define by separation its subset

\begin{equation*} {\texttt{PrfEql}}_0^{\widehat{\sum}}\big((i, x), (j, y)\big) := \big\{p \in {\texttt{PrfEql}}_0^I(i, j) \mid \lambda_{ij}^p(x)= y\big\}. \end{equation*}

Let ${\texttt{refl}}(i, x) := {\texttt{refl}}_i$ , for every $(i, x) \in \widehat{\sum}_{i \in I}\lambda_0 (i)$ . If $p \in {\texttt{PrfEql}}_0^{\widehat{\sum}}\big((i, x), (j, y)\big)$ , then by the condition (iii) of Definition 44 we get $p^{-1} \in {\texttt{PrfEql}}_0^{\widehat{\sum}}\big((j, y), (i, x)\big)$ . If $r \in {\texttt{PrfEql}}_0^{\widehat{\sum}}\big((j, y), (k, z)\big)$ , then by condition (iii) of Definition 44 we have that $p \ast r \in {\texttt{PrfEql}}_0^I{\widehat{\sum}}\big((i, x), (k, z)\big)$ . The clauses of Definition 41 for ${\texttt{PrfEql}}_0^{\widehat{\sum}}\big((i, x), (j, y)\big)$ follow from the corresponding clauses for ${\texttt{PrfEql}}_0^I(i, j)$ .

If $\widehat{I}$ and $\widehat{\sum}_{i \in I}\lambda_0(i)$ are Martin-Löf sets as above, it is straightforward to show that the pair $\widehat{{\texttt{pr}}_1} := \big({\texttt{pr}}_1^{\widehat{\Lambda}}, \varpi_1\big)$ is a map from $\widehat{\sum}_{i \in I}\lambda_0(I)$ to $\widehat{I}$ , where

\begin{equation*} {\texttt{pr}}_1^{\widehat{\Lambda}} \colon \widehat{\sum}_{i \in I}\lambda_0(i) \to I, \ \ \ \ (i,x) \mapsto i; \ \ \ \ i \in I,\ \mbox{and} \end{equation*}

\begin{equation*} \big[\varpi_1\big((i, x),(j, y)\big)\big](p) := p; \ \ \ \ p \in {\texttt{PrfEql}}_0^{\small{\widehat{\sum}}}\big((i, x),(j, y)\big), \end{equation*}

is a function-like first associate of $\widehat{{\texttt{pr}}_1}$ .

Lemma 46. Let $\widehat{X}$ be a Martin-Löf set, $x_0 \in X$ and let ${\texttt{PrfEql}}_0^{x_0}: X \rightsquigarrow \mathbb{V}_0$ be defined by $x \mapsto {\texttt{PrfEql}}_0^X(x, x_0)$ , for every $x \in X$ . Moreover, let

be defined, for every $(x, y) \in D(X)$ , $p \in {\texttt{PrfEql}}_0^X(x, y)$ and $r \in {\texttt{PrfEql}}_0^X(x, x_0)$ , by

\begin{equation*} {\texttt{PrfEql}}_1^{x_0} \big((x, y), p\big) := {\texttt{PrfEql}}_{xy}^{x_0} \colon {\texttt{PrfEql}}_0^X(x, x_0) \to {\texttt{PrfEql}}_0^X(y, x_0) \end{equation*}

\begin{equation*} r \mapsto p^{-1} \ast r. \end{equation*}

Then $\widehat{{\texttt{PrfEql}}^{x_0}} := ({\texttt{PrfEql}}_0^{x_0}, {\texttt{PrfEql}}_1^{x_0})$ is a function-like family of sets over $\widehat{X}$ .

Proof. If $x \in X$ , then ${\texttt{PrfEql}}_{xx}^{{\texttt{refl}}_x}(r) := {\texttt{refl}}_x^{-1} \ast r = {\texttt{refl}}_x \ast r = r$ , for every $r \in {\texttt{PrfEql}}_0^X(x, x_0)$ . If $x =_X y =_X z$ , $p \in {\texttt{PrfEql}}_0^X(x, y), q \in {\texttt{PrfEql}}_0^X(y, z)$ , then for every $r \in {\texttt{PrfEql}}_0^X(x, x_0)$ we have that

\begin{equation*} \big({\texttt{PrfEql}}_{yz}^q \circ {\texttt{PrfEql}}_{xy}^p\big)(r) := q^{-1} \ast (p^{-1} \ast r) = (q^{-1} \ast p^{-1})\ast r =(p \ast q)^{-1} \ast r := {\texttt{PrfEql}}_{xz}^{p \ast q}(r).\end{equation*}

If $p =_{{\texttt{PrfEql}}_0^X(x, y)} p{'}$ , then by Proposition 42(iii) and condition $(\mathrm{ML}_4)$ we get ${\texttt{PrfEql}}_{xy}^p (r) := p^{-1} \ast r = (p{'})^{-1} \ast r := {\texttt{PrfEql}}_{xy}^{p{'}} (r)$ , for every $r \in {\texttt{PrfEql}}_0^X(x, x_0)$ .

Theorem 1. Let $\widehat{X}$ be a proof-relevant set, $x_0 \in X$ and let $\widehat{{\texttt{PrfEql}}^{x_0}} := ({\texttt{PrfEql}}_0^{x_0}, {\texttt{PrfEql}}_1^{x_0})$ be the function-like family of sets over $\widehat{X}$ from Lemma 46. Let $\widehat{\sum}_{x \in X} {\texttt{PrfEql}}_0^X(x, x_0)$ be equipped with its canonical structure of a Martin-Löf set, according to Proposition 45. Then for every $(x, p) \in \widehat{\sum}_{x \in X} {\texttt{PrfEql}}_0^X(x, x_0)$ , we have that

\begin{equation*} (x, p) =_{\small{\widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0^X(x, x_0)}} \big(x_0, {\texttt{refl}}_{x_0}\big).\end{equation*}

Proof. By the definition of equality on the $\sum$ -set of some $\widehat{\Lambda} \in {\texttt{Fam}}(\widehat{I})$ , we have that

\begin{equation*} (x, p) =_{\small{\widehat{\sum}_{x \in X} {\texttt{PrfEql}}_0^X(x, x_0)}} \big(x_0, {\texttt{refl}}_{x_0})\big) :\Leftrightarrow x =_X x_0 \ \& \ \exists_{q \in {\texttt{PrfEql}}_0^X(x, x_0)}\big({\texttt{PrfEql}}_{xx_0}^q(p) = {\texttt{refl}}_{x_0}\big).\end{equation*}

If $(x, p) \in \widehat{\sum}_{x \in X} {\texttt{PrfEql}}_0^X(x, x_0)$ , then $p \in {\texttt{PrfEql}}_0^X(x, x_0)$ , hence $x =_X x_0$ . If we take $q := p$ , then ${\texttt{PrfEql}}_{xx_0}^p(p) := p^{-1} \ast p = {\texttt{refl}}_{x_0}.$

Theorem 1 is a translation of the type-theoretic contractibility of the singleton type (see Coquand 2014) into BST. If M is the judgment (or the term) expressing this contractibility (see also Petrakis 2019d), Martin-Löf’s J-rule trivially implies M, and it is equivalent to M and the transport (see Coquand 2014). In $\mathrm{BISH},$ we do not have the J-rule, but we have transport in a definitional way only. As Theorem 1 indicates, a definitional form of M is provable in BST, although there is no translation of the J-rule in BST. A map between Martin-Löf sets can generate the family of its fibers over its codomain.

Theorem 2. Let $\widehat{X}, \widehat{Y}$ be Martin-Löf sets, and $\widehat{f} := (f, f_1) \colon \widehat{X} \to \widehat{Y}$ a map from $\widehat{X}$ to $\widehat{Y}$ with a function-like first associate $f_1$ .

1. (i) If $y \in Y$ , the pair ${\texttt{PrfEql}} f := \big({\texttt{PrfEql}} f_0^y, {\texttt{PrfEql}} f_1^y\big)$ , where ${\texttt{PrfEql}} f_0^y : X \rightsquigarrow \mathbb{V}_0$ is defined by the rule $x \mapsto {\texttt{PrfEql}}_0^Y(f(x), y),$ , for every $x \in X$ , and

   
   \begin{equation*} {\texttt{PrfEql}} f_1^y\big((x, x{'}), p) := {\texttt{PrfEql}} f_{xx{'}}^{y, p} \colon {\texttt{PrfEql}}_0^Y(f(x), y) \to {\texttt{PrfEql}}_0^Y(f(x{'}), y),\end{equation*}
   \begin{equation*} r \mapsto [f_1(x, x{'}, p)]^{-1} \ast r; \ \ \ \ r \in {\texttt{PrfEql}}_0^Y(f(x), y), \end{equation*}
   is a function-like family of sets over $\widehat{X}$ .

2. (ii) The pair ${\texttt{Prfib}} := ({\texttt{Prfib}}_0, {\texttt{Prfib}}_1)$ , where ${\texttt{Prfib}}_0 : Y \rightsquigarrow \mathbb{V}_0$ is defined by the rule

   \begin{equation*} y \mapsto \widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0^Y(f(x), y); \ \ \ \ y \in Y, \ \ \ \mbox{and} \ \end{equation*}
   
   \begin{equation*} {\texttt{Prfib}}_1^y\big((y, y{'}), q) := {\texttt{Prfib}}_{yy{'}}^{q} : \widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0(f(x), y) \to\widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0^Y(f(x), y{'}), \end{equation*}
   \begin{equation*} (x, p) \mapsto (x, p \ast q); \ \ \ \ (x, p) \in \widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0^Y(f(x), y), \end{equation*}
   is a function-like family of sets over $\widehat{Y}$ .

Proof. (i) If $r \in {\texttt{PrfEql}}_0^Y(f(x), y)$ , then by Proposition 42(iii) we get

\begin{equation*} {\texttt{PrfEql}}_0 f_{xx{'}}^{y, {\texttt{refl}}_x}(r) := [f_1(x, x, {\texttt{refl}}_x)]^{-1} \ast r = \big[{\texttt{refl}}\big(f(x)\big)\big]^{-1} \ast r= {\texttt{refl}}\big(f(x)\big) \ast r = r. \end{equation*}

If $p \in {\texttt{PrfEql}}_0^X(x, x{'})$ and $p{'} \in {\texttt{PrfEql}}_0^X(x{'}, x{''})$ , then for every $r \in {\texttt{PrfEql}}_0^Y(f(x), y)$ , we get

\begin{align*}{\texttt{PrfEql}}_0 f_{x{'}x{''}}^{y, p{'}}\bigg({\texttt{PrfEql}}_0 f_{xx{'}}^{y, p}(r)\bigg) & = [f_1(x{'}, x{''}, p{'})]^{-1} \ast\big( [f_1(x, x{'}, p)]^{-1} \ast r\big)\\& = \big([f_1(x{'}, x{''}, p{'})]^{-1} \ast [f_1(x, x{'}, p)]^{-1}\big) \ast r\\& = [f_1(x, x{'}, p) \ast f_1(x{'}, x{''}, p{'}) ]^{-1} \ast r\\& = [f_1(x, x{''}, p \ast q)]^{-1} \ast r\\& := {\texttt{PrfEql}}_0 f_{xx{''}}^{y, p \ast p{'}}(r).\end{align*}

If $p =_{{\texttt{PrfEql}}_0^X(x, x{'})} s$ , and if $r \in {\texttt{PrfEql}}_0^Y(f(x), y)$ , by the function-likeness ⁵ of $f_1$ , we get

\begin{equation*} {\texttt{PrfEql}}_0 f_{xx{'}}^{y, p}(r) := [f_1(x, x{'}, p)]^{-1} \ast r = [f_1(x, x{'}, s)]^{-1} \ast r := {\texttt{PrfEql}}_0 f_{xx{'}}^{y, s}(r).\end{equation*}

(ii) First, we show that for every $p, p{'} \in {\texttt{PrfEql}}_0^Y(f(x), y),$ we have that

(1) \begin{equation}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ p =_{\small{ {\texttt{PrfEql}}_0^Y(f(x), y)}} p{'} \Rightarrow (x, p)=_{\small{\widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0^Y(f(x), y)}} (x, p{'}),\end{equation}

since

\begin{equation*} {\texttt{PrfEql}}_0 f_{xx}^{y, {\texttt{refl}}_x}(p) := [f_1(x, x, {\texttt{refl}}_x)]^{-1} \ast p = [{\texttt{refl}}_{f(x)}]^{-1} \ast p= {\texttt{refl}}_{f(x)} \ast p = p = q.\end{equation*}

If $y \in Y$ , then by (1), for every $(x, p) \in \widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0^Y(f(x), y)$ , we get

\begin{equation*} {\texttt{Prfib}}_{yy}^{{\texttt{refl}}_y}(x, p) := \big(x, p \ast {\texttt{refl}}_y\big)=_{\small{\widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0^Y(f(x), y)}} (x, p).\end{equation*}

If $q \in {\texttt{PrfEql}}_0^Y(y, y{'}$ and $q{'} \in {\texttt{PrfEql}}_0^Y(y{'}, y{''})$ , then for every $(x, p) \in \widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0^Y(f(x), y)$

\begin{equation*} {\texttt{Prfib}}_{y{'}y{''}}^{q{'}}\bigg({\texttt{Prfib}}_{yy{'}}^{q}(x, p)\bigg) := {\texttt{Prfib}}_{y{'}y{''}}^{q{'}}(x, p \ast q):= (x, (p \ast q) \ast q{'}\big)\end{equation*}

\begin{equation*} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\stackrel{(1)} = (x, p \ast (q \ast q{'}):= {\texttt{Prfib}}_{yy{''}}^{q \ast q{'}}(x, p).\end{equation*}

If $q =_{\small{{\texttt{PrfEql}}_0^Y(y, y{'})}} s$ , then ${\texttt{Prfib}}_{yy{'}}^{q} = {\texttt{Prfib}}_{yy{'}}^{s}$ , since for every $(x, p) \in \widehat{\sum}_{x \in X}{\texttt{PrfEql}}_0^Y(f(x), y)$

\begin{equation*} {\texttt{Prfib}}_{yy{'}}^{q}(x, p) := (x, p \ast q) \stackrel{(1)} = (x, p \ast s) :={\texttt{Prfib}}_{yy{'}}^{s}(x, p).\end{equation*}

12. Contractible Sets and Subsingletons in BST

Next follow some results on contractible sets and subsingletons in BST that translate results from Chapters 3 and 4 of book-HoTT. According to Definition 5(iv), in $\mathrm{BST},$ the truncation $||X||$ of a set X is the same totality X equipped with a new equality, while in HoTT is a higher inductive type.

Proposition 47. If $(f, g) : X =_{\mathbb{V}_0} Y$ , then $(f^*, g^*) : \mathbb{F}(Z, X) =_{\mathbb{V}_0} \mathbb{F}(Z, Y)$ , where the operations $f^* \colon \mathbb{F}(Z,X) \rightsquigarrow \mathbb{F}(Z,Y)$ and $g^* \colon \mathbb{F}(Z,Y) \rightsquigarrow \mathbb{F}(Z,X)$ are defined, respectively, by the commutativity of the following diagrams

Proof. Clearly, the operations $f^*$ and $g^*$ are functions. If $k \in \mathbb{F}(Z,Y)$ and $h \in \mathbb{F}(Z,X)$ , then $f^*(g^*(k)) := f^*(g \circ k) := f \circ (g \circ k) := (f \circ g) \circ k := \mathrm{id}_Y \circ k := k$ , and $g^*(f^*(h)) := g^*(f \circ h) := g \circ (f \circ h) := (g \circ f) \circ h := \mathrm{id}_X \circ h := h$ .

Proposition 47 is an example of a result in BST the analogue of which in HoTT is shown with the axiom of univalence ${\texttt{UA}}$ in The Univalent Foundations Program (2013) (the axiom FunExt can also be used instead).

Proposition 48. If X is a set, the following are equivalent:

1. (i) X is contractible.

2. (ii) X is an inhabited subsingleton.

3. (iii) $X =_{\mathbb{V}_0} \pmb{1}$ .

Proof.

1. (i) $\Rightarrow$ (ii) If $x_0$ is a centre of contraction for X, then $x_0$ inhabits X. If $x, y \in X$ , then $x =_X x_0$ and $y =_X x_0$ , hence $x =_X y$ .

2. (ii) $\Rightarrow$ (iii) Let $f \colon X \rightsquigarrow \pmb{1}$ , defined by $f(x) := 0$ , for every $x \in X$ , and $g \colon \pmb{1} \colon X$ , defined by $g(0) := x_0$ , where $x_0$ inhabits X. Clearly, these operations are functions, and $(f,g) \colon X =_{\mathbb{V}_0} \pmb{1}$ .

3. (iii) $\Rightarrow$ (i) Let $f \in \mathbb{F}(X, \pmb{1})$ and $g \in \mathbb{F}(\pmb{1}, X)$ such that $(f,g) \colon X =_{\mathbb{V}_0} \pmb{1}$ . If $x \in X$ , then $x =_X g(f(x)) := g(0) \in X$ . hence g(0) is a center of contraction for X.

Remark 49. As any set can be truncated and become a subsingleton (see Definition 4(iv)), the previous proposition provided numerous examples of contractible sets. Namely, any inhabited set can be turned into a contractible set through the truncation of its equality.

Proposition 50. Let $\Lambda := (\lambda_0, \lambda_1) \in {\texttt{Fam}}(I)$ .

1. (i) If is a modulus of centres of contraction for $\lambda_0$ , i.e., $\Theta_i$ is a center of contraction for $\lambda_0(i)$ , then $\Theta \in \prod_{i \in I}\lambda_0(i)$ is a center of contraction for $\prod_{i \in I}\lambda_0(i)$ and $\sum_{i \in I} \lambda_0(i) =_{\mathbb{V}_0} I$ .

2. (ii) If $i_0 \in I$ is a center of contraction for I, then $\sum_{i \in I} \lambda_0(i)=_{\mathbb{V}_0} \lambda_0(i_0)$ .

Proof.

1. (i) If $i =_I j$ , then $\Theta_j =_{\lambda_0(j)} \lambda_{ij}(\Theta_i)$ , as $\Theta_j$ is a centre of contraction for $\lambda_0(j)$ . If $\Phi \in \prod_{i \in I}\lambda_0(i)$ , then $\Phi_i =_{\lambda_0(i)} \Theta_i$ , for every $i \in I$ , hence $\Phi =_{\small{\prod_{i \in I}\lambda_0(i)}} \Theta$ . Let $f \colon I \rightsquigarrow \sum_{i \in I}\lambda_0(i)$ , defined by $f(i) := (i, \Theta_i)$ , for every $i \in I$ . It is immediate to show that f is a function, and $\big({\texttt{pr}}_1^{\Lambda}, f\big) \colon \sum_{i \in I} \lambda_0(i) =_{\mathbb{V}_0} I$ .

2. (ii) Let $g \colon \lambda_0(i_0) \rightsquigarrow \sum_{i \in I}\lambda_0(i)$ , defined by $g(x) := (i_0, x)$ , for every $x \in \lambda_0(i_0)$ , and $h \colon \sum_{i \in I}\lambda_0(i) \rightsquigarrow \lambda_0(i_0)$ , defined by $h(i, x) := \lambda_{ii_0}(x)$ , for every $(i, x) \in \sum_{i \in I}\lambda_0(i)$ . It is straightforward to show that g, h are functions and $(g, h) \colon\sum_{i \in I} \lambda_0(i) =_{\mathbb{V}_0} \lambda_0(i_0)$ .

Proposition 51. Let $\Lambda := (\lambda_0, \lambda_1) \in {\texttt{Fam}}(I)$ , a modulus of centers of contraction for $\lambda_0$ , and X, Y sets.

1. (i) If $h \colon I \rightsquigarrow \sum_{i \in I}\lambda_0(i)$ is defined by $h(i) := \big(i, \Theta_i\big)$ , for every $i \in I$ , then h is a function and $({\texttt{pr}}_1^{\Lambda}, h)\colon \sum_{i \in I}\lambda_0(i) =_{\mathbb{V}_0} I$ .

2. (ii) $\mathbb{F}\big(I, \sum_{i \in I}\lambda_0(i)\big) =_{\mathbb{V}_0} \mathbb{F}(I, I)$ .

3. (iii) If X is contractible and Y is a retract of X, then Y is contractible.

Proof. The proof of (i) is straightforward and (ii) follows from (i) and Proposition 47. For the proof of the next theorem though, we write explicitly the witnesses of the required equality in $\mathbb{V}_0$ , which are the witnesses provided by the proof of Proposition 47. Let $\phi \colon \mathbb{F}(I, \sum_{i \in I}\lambda_0(i)) \rightsquigarrow \mathbb{F}(I, I)$ , defined by the rule $f \mapsto \phi(f)$ , where $\phi(f) := {\texttt{pr}}_1^{\Lambda} \circ f$

Clearly, $\phi$ is a function. Let $\theta \colon \mathbb{F}(I, I) \rightsquigarrow \mathbb{F}(I, \sum_{i \in I}\lambda_0(i))$ , defined by the rule $g \mapsto \theta(g)$ , where $\theta(g) := h \circ g$ , where h is defined in case (i). Clearly, $\theta$ is a function. It is straightforward to show that $(\phi, \theta) \colon \mathbb{F}\big(I, \sum_{i \in I}\lambda_0(i)\big) =_{\mathbb{V}_0} \mathbb{F}(I, I)$ .

(iii) Let $r \colon X \to Y$ and $s \colon Y \to X$ such that $r \circ s = \mathrm{id}_Y$ . It is immediate to show that if $x_0 \in X$ is a center of contraction for X, then $r(x_0)$ is a center of contraction for Y.

Theorem 3. Let $\Lambda := (\lambda_0, \lambda_1) \in {\texttt{Fam}}(I)$ , and let be a modulus of centers of contraction for $\lambda_0$ . If $(\phi, \theta) \colon \mathbb{F}\big(I, \sum_{i \in I}\lambda_0(i)\big) =_{\mathbb{V}_0} \mathbb{F}(I, I)$ , where $\phi$ and $\theta$ are defined in the proof of Proposition 51(ii), then $\prod_{i \in I}\lambda_0(i)$ is a retract of ${\texttt{fib}}^{\phi}(\mathrm{id}_I)$ .

Proof. By Definition 6, we have that

\begin{equation*}{\texttt{fib}}^{\phi}(\mathrm{id}_I) := \big\{ f \in \mathbb{F}\big(I, \sum_{i \in I}\lambda_0(i)\big) \mid \phi(f)=_{\mathbb{F}(I, I)}\mathrm{id}_I\big\}.\end{equation*}

We need to find functions $r^{\phi} \colon {\texttt{fib}}^{\phi}(\mathrm{id}_I) \to \prod_{i \in I}\lambda_0(i)$ and $s^{\phi} \colon\prod_{i \in I}\lambda_0(i) \to {\texttt{fib}}^{\phi}(\mathrm{id}_I)$ such that the following diagram commutes

Let the operation $r^{\phi} \colon {\texttt{fib}}^{\phi}(\mathrm{id}_I) \rightsquigarrow \prod_{i \in I}\lambda_0(i)$ , defined by the rule $f \mapsto r^{\phi}(f)$ , where

As $\phi(f) := {\texttt{pr}}_1^{\Lambda} \circ f = \mathrm{id}_I$ , we get $[\phi(f)](i) := {\texttt{pr}}_1^{\Lambda}(f(i)) =_I i$ , hence $\big[r^{\phi}(f)\big]_i \in \lambda_0(i)$ , for every $i \in I$ . Next we show that $r^{\phi}(f) \in \prod_{i \in I}\lambda_0(i)$ . If $i =_I j$ , then $f(i)=_{\small{\sum_{i \in I}\lambda_0(i)}} f(j)$ , and hence

\begin{equation*}{\texttt{pr}}_1^{\Lambda}(f(i)) =_I {\texttt{pr}}_1^{\Lambda}(f(j)) \ \ \ \& \ \ \ \lambda_{{\texttt{pr}}_1^{\Lambda}(f(i)){\texttt{pr}}_1^{\Lambda}(f(j))}\big({\texttt{pr}}_2^{\Lambda}(f(i)) =_{\small{\lambda_0({\texttt{pr}}_1^{\Lambda}(f(j)))}}{\texttt{pr}}_2^{\Lambda}(f(j)). \end{equation*}

Therefore,

\begin{align*}\lambda_{ij}\big(\big[r^{\phi}(f)\big]_i\big) & :=\lambda_{ij}\bigg(\lambda_{{\texttt{pr}}_1^{\Lambda}(f(i))i}\bigg({\texttt{pr}}_2^{\Lambda}\big(f(i)\big)\bigg)\bigg)\\& = \lambda_{{\texttt{pr}}_1^{\Lambda}(f(i))j}\bigg({\texttt{pr}}_2^{\Lambda}\big(f(i)\big)\bigg)\\& = \lambda_{{\texttt{pr}}_1^{\Lambda}(f(j))j}\bigg(\lambda_{{\texttt{pr}}_1^{\Lambda}(f(i)){\texttt{pr}}_1^{\Lambda}(f(j))}\bigg({\texttt{pr}}_2^{\Lambda}(f(i))\bigg)\bigg)\\& = \lambda_{{\texttt{pr}}_1^{\Lambda}(f(j))j}\bigg( {\texttt{pr}}_2^{\Lambda}(f(j))\bigg)\\& := \big[r^{\phi}(f)\big]_j.\end{align*}

Next we show that $r^{\phi}$ is a function. If $f = g$ and $i \in I$ , then $f(i)=_{\small{\sum_{i \in I}\lambda_0(i)}} g(i)$ , i.e.,

\begin{equation*}{\texttt{pr}}_1^{\Lambda}(f(i)) =_I {\texttt{pr}}_1^{\Lambda}(g(i)) \;\;\; \& \;\;\; \lambda_{{\texttt{pr}}_1^{\Lambda}(f(i)) {\texttt{pr}}_1^{\Lambda}(g(i))}\big({\texttt{pr}}_2^{\Lambda}(f(i))=_{\small{\lambda_0({\texttt{pr}}_1^{\Lambda}(g(i)))}} {\texttt{pr}}_2^{\Lambda}(g(i)). \end{equation*}

Therefore,

\begin{align*}\big[r^{\phi}(f)\big]_i :& = \lambda_{{\texttt{pr}}_1^{\Lambda}(f(i))i}\bigg({\texttt{pr}}_2^{\Lambda}\big(f(i)\big)\bigg)\\& = \lambda_{{\texttt{pr}}_1^{\Lambda}(g(i))i}\bigg(\lambda_{{\texttt{pr}}_1^{\Lambda}(f(i)){\texttt{pr}}_1^{\Lambda}(g(i))}\bigg({\texttt{pr}}_2^{\Lambda}(f(i))\bigg)\bigg)\\& = \lambda_{{\texttt{pr}}_1^{\Lambda}(g(i))i}\bigg( {\texttt{pr}}_2^{\Lambda}(g(i))\bigg)\\& := \big[r^{\phi}(g)\big]_i.\end{align*}

Let the operation $s^{\phi} \colon \prod_{i \in I}\lambda_0(i) \rightsquigarrow {\texttt{fib}}^{\phi}(\mathrm{id}_I)$ , defined by the rule $\Theta \mapsto s^{\phi}(\Theta)$ , where

\begin{equation*} s^{\phi}(\Theta) \colon I \rightsquigarrow \sum_{i \in I}\lambda_0(i), \ \ \ \ \big[s^{\phi}(\Theta)\big](i):= (i, \Theta_i); \ \ \ \ i \in I. \end{equation*}

First we show that $s^{\phi}(\Theta)$ is a function. If $i =_I j$ , then $(i, \Theta_i)=_{\small{\sum_{i \in I}\lambda_0(i)}} (j, \Theta_j)$ , as the equality $\Theta_j=_{\lambda_0(j)} \lambda_{ij}(\Theta)$ follows from the hypothesis $\Theta \in \prod_{i \in I}\lambda_0(i)$ . To show $s^{\phi}(\Theta) \in {\texttt{fib}}^{\phi}(\mathrm{id}_I)$ , let $i \in I$ , and then $\big(\phi\big(s^{\phi}(\Theta)\big)\big](i) := {\texttt{pr}}_1^{\Lambda}(i, \Theta_i) := i$ . To show that $s^{\phi}$ is a function, let $\Theta =_{\prod_{i \in I}\lambda_0(i)} \Theta{'}$ . If $i \in I$ , then $[s^{\phi}(\Theta)](i) := (i, \Theta_i) = (i, \Theta{'}_i) := [s^{\phi}(\Theta{'})](i)$ . Finally, we show the commutativity of the initial diagram in the proof. If $i \in I$ , then

\begin{align*}\big[r^{\phi}\big(s^{\phi}(\Theta)\big)\big]_i & :=\lambda_{{\texttt{pr}}_1^{\Lambda}\big([s^{\phi}(\Theta)](i)\big)i}\bigg({\texttt{pr}}_2^{\Lambda}\big(\big[s^{\phi}(\Theta)\big](i)\big)\bigg)\\& := \lambda_{{\texttt{pr}}_1^{\Lambda}(i, \Theta_i)i}\big({\texttt{pr}}_2^{\Lambda}(i, \Theta_i)\big)\\& := \lambda_{ii}(\Theta_i)\\& := \Theta_i.\end{align*}

Theorem 3 is the translation of Theorem 4.9.4 in book-HoTT, where in the hypothesis of the latter the universe is univalent.

Corollary 52. If $\Lambda := (\lambda_0, \lambda_1) \in {\texttt{Fam}}(I)$ and is a modulus of centers of contraction for $\lambda_0$ , then $\Theta$ is center of contraction for $\prod_{i \in I}\lambda_0(i)$ .

Proof. Since $(\phi, \theta) \colon \mathbb{F}\big(I, \sum_{i \in I}\lambda_0(i)\big) =_{\mathbb{V}_0} \mathbb{F}(I, I)$ , by Proposition 7 the set ${\texttt{fib}}^{\phi}(\mathrm{id}_I)$ is contractible and $\theta(\mathrm{id}_I) := h \circ \mathrm{id}_I := h$ is a center of contraction for ${\texttt{fib}}^{\phi}(\mathrm{id}_I)$ , where h is defined in Proposition 51(i). As $r^{\phi} \colon {\texttt{fib}}^{\phi}(\mathrm{id}_I) \to \prod_{i \in I}\lambda_0(i)$ is a retraction, by the proof of Proposition 51(iv) we have that $\prod_{i \in I}\lambda_0(i)$ is contractible and $r^{\phi}(h)$ is a center of contraction for $\prod_{i \in I}\lambda_0(i)$ . If $i \in I$ , then $ \big[r^{\phi}(h)\big]_I := \lambda_{{\texttt{pr}}_1^{\Lambda}(h(i))i}\big({\texttt{pr}}_2^{\Lambda}(h(i))\big) :=\lambda_{ii}(\Theta_i) := \Theta_i$ , hence $r^{\phi}(h) := \Theta$ .

Corollary 52 is the translation in BST of the fact that ${\texttt{UA}}$ implies the principle of weak function extensionality.

Proposition 53. Let $||X||$ be the truncation of X, Y, Z subsingletons, and E a set.

1. (i) If $f \in \mathbb{F}(Y, Z)$ and $g \in \mathbb{F}(Z, Y)$ , then $(f, g) \colon Y =_{\mathbb{V}_0} Z$ .

2. (ii) If X is inhabited, then $||X||$ is inhabited.

3. (iii) If $f \colon X \to E$ , there is $||f|| \colon ||X|| \to ||E||$ , such that $||f||(x) := f(x)$ , for every $x \in X$ .

4. (iv) $Y =_{\mathbb{V}_0} ||Y||$ .

Proof. (i) and (ii) follow immediately from cases (iv) and (i) nof Definition 4. For the proof of (iii), we define the operation $||f|| \colon ||X|| \rightsquigarrow ||E||$ by the rule $||f||(x) := f(x)$ , for every $x \in X$ . As $||E||$ is a subsingleton, if $x \ \small{\small{\lvert \lvert =_X \rvert \rvert}} \ x{'}$ , then $||f||(x) := f(x) \ \small{\small{\lvert \lvert =_E \rvert \rvert}} \ f(x{'}):= ||f||(x{'})$ , and $||f||$ is a function. For the proof of (iv), it is straightforward to show that the operations of type $Y \to ||Y||$ and $||Y|| \to Y$ , defined by the identity map rule, respectively, are functions that witness the equality $Y =_{\mathbb{V}_0} ||Y||$ .

Corollary 54. Let $\Lambda := (\lambda_0, \lambda_1) \in {\texttt{Fam}}(I)$ .

1. (i) $||\Lambda|| := \big(||\lambda_0||, ||\lambda_1||) \in {\texttt{Fam}}(I)$ , where $||\lambda_0||(i)\colon I \rightsquigarrow \mathbb{V}_0$ is defined by

   \begin{equation*} ||\lambda_0||(i) := ||\lambda_0(i)||; \ \ \ \ i \in I, \ \ \ \mbox{and} \end{equation*}
   \begin{equation*} ||\lambda_1||(i,j) := ||\lambda||_{ij} \colon ||\lambda_0(i)|| \to ||\lambda_0(j)||, \ \ \ \||\lambda||_{ij} := ||\lambda_{ij}||; \ \ \ \ (i,j) \in D(I).\end{equation*}

2. (ii) (ii) If $\lambda_0(i)$ is a subsingleton, for every $i \in I$ , and $\Theta \colon\prod_{i \in I}||\lambda_0(i)||$ , then $\Theta \colon \prod_{i \in I}\lambda_0(i)$ .

3. (iii) If $\lambda_0(i)$ is a subsingleton, for every $i \in I$ , then $\prod_{i \in I}\lambda_0(i)$ is a subsingleton.

Proof.

1. (i) To show that $||\lambda||_{ij}$ is well defined, we use Proposition 53(iii). To show the properties of a family of sets over I for $||\Lambda||$ , we use the corresponding properties for $\Lambda$ .

2. (ii) By case (i), if $i =_I j$ , then $\Theta_j \in ||\lambda_0(j)||$ . As $||\lambda_0(j)||$ is the set $\lambda_0(j)$ , we get $\Theta_j \in \lambda_0(j)$ . Since $\lambda_0(j)$ is a subsingleton, we get $\Theta_i) =_{\lambda_0(j)} \lambda_{ij}(\Theta_i)$ .

3. (iii) It follows immediately from the definition of the canonical equality on $\prod_{i \in I}\lambda_0(i)$ .

13. Concluding Comments

According to Feferman (see Feferman 1979, p. 207), the formal, or internal realisability interpretation of the language $\mathfrak{L}(T)$ of a formal theory T in the language $\mathfrak{L}(T{'})$ of a formal theory T’, is an assignment $ \phi \mapsto f \ \boldsymbol r \ \phi $ of any formula $\phi$ of $\mathfrak{L}(T)$ to a formula $\phi_r :\Leftrightarrow f \ \boldsymbol r \ \phi$ in $\mathfrak{L}(T{'})$ , where $\phi_r$ has at most one additional free variable f. This interpretation is sound if

\begin{equation*} T \vdash \phi \Rightarrow \exists_{\tau \in {\texttt{Term}}(\mathfrak{L}(T{'}))}\big(T{'} \vdash\tau \ \boldsymbol r \ \phi\big), \end{equation*}

for every formula $\phi$ of $\mathfrak{L}(T)$ . The added axiom-scheme $(\mathrm{A{-}r})$ “to assert is to realize”

\begin{equation*} \phi \Leftrightarrow \exists_f\big(f \ \boldsymbol r \ \phi\big), \end{equation*}

which expresses the equivalence of the assertion of $\phi$ with its realizability, reflects the basic tenet of constructive reasoning that a statement is to be asserted only if it is proved. Note that in Feferman’s refined theory with MwE, the axiom-scheme $(\mathrm{A{-}r})$ implies the principle of dependent choice DC and the presentation axiom! (see Feferman 1979, pp. 214–215). It is also expected that one can show inductively that the scheme $(\mathrm{A{-}r})$ is itself realisable in some theory S, i.e.,

\begin{equation*} \forall_{\phi}\exists_{\tau}\bigg(S \vdash \tau \ \boldsymbol r \ \big[\phi \Leftrightarrow \exists_f\big(f \ \boldsymbol r \ \phi\big)\big]\bigg). \end{equation*}

In the informal, or external realisability interpretation of $\mathfrak{L}(T),$ one defines a relation $R(f, \phi)$ between mathematical objects f of some sort and a formula $\phi$ . For example, Kleene defined such a relation for $f \in {\mathbb N}$ and $\phi$ a formula of arithmetic. External realisability interpretations can often be regarded as the reading of a formal $f \ \boldsymbol r \ \phi$ in a specific model.

Here we described an external realizability interpretation of some part of the language of the informal theory BISH in itself, where the corresponding realisability relation is

\begin{equation*} {\texttt{Prf}}(p, \phi) :\Leftrightarrow p \in {\texttt{Prf}}(\phi). \end{equation*}

Why one would choose to work within an informal framework? Maybe because to realise some formula $\phi$ does not necessarily imply that $\phi$ is constructively acceptable. For example, in Feferman (1979), pp. 207–208, Feferman defined a formal realisability interpretation of $\mathfrak{L}(T_0)$ in itself such that the corresponding axiom scheme $(\mathrm{A{-}r})$ implies the full axiom of choice. Moreover, even if one works with a realisability interpretation that avoids the realisability of the full AC, it is not certain that whatever this theory realises is constructively acceptable, or faithful to some motivating informal constructive theory like BISH. For example, the realisability of the presentation axiom in $T_0^*$ , which holds also in the setoid-interpretation of Bishop sets in intensional MLTT, does not make it necessarily constructively acceptable. In the informal level of BISH, there is no reason to accept it.

If the main philosophical question regarding Bishop-style constructive mathematics $(\mathrm{BCM})$ , in general, is “what is constructive?,” an answer provided from a formal treatment of BCM that cannot be “captured” by BISH itself, is not necessarily the “right” answer.

In Feferman (1979), p. 177, Feferman criticises Bishop for a “certain casualness about mentioning the witnessing information. $\ldots$ one is looser in practice in order to keep that from getting too heavy. Practice then looks very much like everyday analysis and it is hard to see what the difference is unless one takes the official definitions seriously.” In our opinion, Feferman is right on spotting this casualness in Bishop’s account, which is though on purpose, as Bishop’s crucial comment in Bishop (1970), p. 67 shows. One could also say that, if the difference between constructive analysis and everyday, classical analysis is difficult to see, then this is an indication of the success of Bishop’s way of writing. What we find that is missing when some official definitions are not taken seriously is the proof-relevant character of Bishop’s analysis and its proximity to proof-relevant mathematical analysis, like analysis within MLTT. An important consequence of revealing the witnessing information is the avoidance of choice.

The use of the axiom of choice in constructive mathematics is an indication of missing data. As we have seen already in many cases, and also in Example 9.6, the inclusion of witnessing data, like a modulus of some sort, facilitates the avoidance of choice in the corresponding constructive proof. The standard view regarding the use of choice in BISH is that some weak form of choice, countable choice, or dependent choice is necessary. This is certainly true when the witnessing data are ignored. Richman criticised the use of countable choice in BISH (see Richman 2001, and also Schuster 2004). The revealing of witnessing data or not in BISH “oscillates” between the two extremes, regarding proof-relevance, which are also the two extremes, regarding choice. The first extreme is classical mathematics based on ZFC, where the complete lack of proof-relevance is combined with the use of a powerful choice axiom, and the second extreme is type-theoretic mathematics based on intensional MLTT, where proof-relevance is “everywhere” and the axiom of choice,i.e., the distributivity of $\sum$ over $\prod$ , is provable! When the witnessing data are ignored, then some form of weak choice is necessary for BISH, while when the witnessing data are highlighted, then choice is avoided. A similar phenomenon occurs in univalent type theory. The univalent version of the axiom of choice, in the formulation of which truncation is involved, is not provable. And what truncation does is to suppress the evidence.

Next follow some topics related to the proof-relevant character of BISH that need to be addressed in the future.

1. (1) A BHK-interpretation of a negated formula $\neg \phi$ is missing from Definitions 34 and 35. As negated formulas are rare in BISH (see Petrakis 2022b; Petrakis and Wessel to appear), we find safer at the moment to exclude them from our account of a BHK-interpretation of BISH. If ${\texttt{Prf}}(\phi)$ is given, and we apply the rule of implication for $\neg \phi :\Leftrightarrow \phi \Rightarrow \bot$ , then ${\texttt{Prf}}(\neg \phi) := \mathbb{F}\big({\texttt{Prf}}(\phi), {\texttt{Prf}}(\bot)\big)$ . If we accept the clause of the naive BHK-interpretation that $\bot$ has no witness, then we need to state ${\texttt{Prf}}(\bot) := \emptyset$ , and then we get ${\texttt{Prf}}(\neg \phi) := \mathbb{F}\big({\texttt{Prf}}(\phi), \emptyset)\big)$ . As the use of the empty (sub) set ⁶ in BISH is problematic (see Bishop and Bridges 1985, p. 69), so is the status of the object $\mathbb{F}\big({\texttt{Prf}}(\phi), \emptyset)\big)$ .

2. (2) Through the notion of set with a proof-relevant equality, Voevodsky’s notion of 0-set can be formulated in BST. We need the notion of Martin-Löf set with an inhabited proof-relevant structure to translate some basic facts from Voevodsky’s theory of 0-sets in BST. A first step in this direction is taken in Petrakis (2020 c, Section 5.6).

3. (3) Further results from book-HoTT can be translated in BISH through BST. For example, Lemmata 4.8.1 and 4.8.2 in book-HoTT take the following form in BST. If $\widehat{\Lambda} := (\lambda_0, \lambda_1) \in {\texttt{Fam}}(\widehat{I})$ , where $\widehat{I}$ is a Martin-Löf set, then, for every $i \in I$ , we have that ${\texttt{fib}}^{{\texttt{pr}}_1^{\widehat{\Lambda}}}(i) =_{\mathbb{V}_0} \lambda_0(i)$ , while if $\widehat{f} : \widehat{X} \to \widehat{Y}$ , then $X =_{\mathbb{V}_0} \widehat{\sum}_{y \in Y}{\texttt{fib}}^{f}(y)$ . Following the book-HoTT, we can use the translation of the “left universal property of identity types” in BST, namely the equality

   \begin{equation*}\bigg(\sum_{j \in I}\sum_{p \in {\texttt{PrfEql}}_0^I(j,i)}\lambda_0(j)\bigg) =_{\mathbb{V}_0} \lambda_0(i).\end{equation*}

4. (4) Martin-Löf sets need to be studied further. ⁷ For example, families of Martin-Löf set over some Martin-Löf set $\widehat{I}$ can be studied within BST.

As we have tried to show in this paper, the proof-relevance of BISH is not a priori part of it, but it can be revealed a posteriori. In MLTT and its univalent extensions though, proof-relevance is a priori part of them, and many facts are generated or hold automatically by the presence of the J-rule, or the univalence axiom of Voevodsky.⁸ Through BST interesting “parts” of type-theoretic concepts and results can be translated to BISH in a “definitional,” nonaxiomatic way.