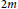1 results
Injectivity of Generalized Wronski Maps
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 4 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 747-761
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation