Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T12:47:52.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Injectivity of Generalized Wronski Maps

Published online by Cambridge University Press:  20 November 2018

Yanhe Huang ,
Frank Sottile  and
Igor Zelenko
Yanhe Huang
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, USA e-mail: [email protected]
Frank Sottile
Affiliation:
Department of Mathematics, Texas A & M University, College Station, Texas 77843, USA e-mail: [email protected]@math.tamu.edu
Igor Zelenko
Affiliation:
Department of Mathematics, Texas A & M University, College Station, Texas 77843, USA e-mail: [email protected]@math.tamu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study linear projections on Plücker space whose restriction to the Grassmannian is a non-trivial branched cover. When an automorphism of the Grassmannian preserves the fibers, we show that the Grassmannian is necessarily of $m$-dimensional linear subspaces in a symplectic vector space of dimension 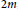$2m$, and the linear map is the Lagrangian involution. The Wronski map for a self-adjoint linear diòerential operator and the pole placement map for symmetric linear systems are natural examples.

Keywords

14M1534A3093B55Wronski mapPlücker embeddingcurves in Lagrangian Grassmannianself-adjoint linear differential operatorsymmetric linear control systempole placement map
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 4 , 01 December 2017 , pp. 747 - 761
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Arnol'd, V., On the number of flattening points on space curves. Sinai's Moscow Seminar on Dynamical Systems, Amer. Math. Soc. Transl. Ser. 2,171, American Mathematical Society, 1996, pp. 11–22.Google Scholar
[2] Arnol'd, V., Sturm theorems and symplectic geometry. Funktsional. Anal, i Prilozhen. 19(1985), no. 4, 1–10,95. http://dx.doi.org/10.1007/BF01086018 Google Scholar
[3] Byrnes, C. I., Algebraic and geometric aspects of the analysis of feedback systems. In: Geometrical methods for the study of linear systems, NATO Adv. Study Inst. Ser., Ser. C: Math. Phys. Sci., 62, Reidel, Dordrecht-Boston, Mass., 1980, pp. 85–124.Google Scholar
[4] Chow, W.-L., On the geometry of algebraic homogeneous spaces. Ann. of Math. (2) 50(1949), 32–67. http://dx.doi.org/10.2307/1 969351 Google Scholar
[5] Delchamps, D. E., State space and input-output linear systems. Springer-Verlag, New York, 1988. http://dx.doi.org/10.1007/978-1 -4612-381 6-4 Google Scholar
[6] Doubrov, B., Contact trivialization of ordinary differential equations. In: Differential geometry and its applications (Opava, 2001), Math. Publ., 3, Silesian Univ. Opava, Opava, 2001, pp. 73–84.Google Scholar
[7] Doubrov, B. and I. Zelenko, On local geometry of non-holonomic rank 2 distributions. J. Lond. Math. Soc. (2) 80(2009), no. 3, 545–566. http://dx.doi.org/10.1112/jlms/jdpO44 Google Scholar
[8] Doubrov, B., Equivalence of variational problems of higher order. Differential Geom. Appl. 29(2011), no. 2, 255–270. http://dx.doi.org/10.101 6/j.difgeo.2010.12.004 Google Scholar
[9] Doubrov, B., On geometry ofaffine control systems with one input. In: Geometric control theory and sub-Riemannian geometry, Springer INdAM Ser., 5, Springer, Cham, 2014, pp. 133–152. http://dx.doi.org/10.1007/978-3-31 9-02132-4_9 Google Scholar
[10] Eisenbud, D. and J. Harris, Divisors on general curves and cuspidal rational curves. Invent. Math. 74(1983), 371–418. http://dx.doi.org/10.1007/BF01394242 Google Scholar
[11] Eisenbud, D., When ramification points meet. Invent. Math. 87(1987), 485–493. http://dx.doi.org/10.1007/BF01389239 Google Scholar
[12] Eremenko, A. and A. Gabrielov, Rational functions with real critical points and the B. and M. Shapiro conjecture in real enumerative geometry. Ann. of Math. (2) 155(2002), no. 1,105-129. http://dx.doi.org/10.2307/3062151 Google Scholar
[13] Fuhrmann, P. A., On symmetric rational transfer functions. Linear Algebra Appl. 50(1983), 167–250. http://dx.doi.org/1 0.101 6/0024-3795(83)90057-5 Google Scholar
[14] Goodman, R. and Wallach, N. R., Representations and invariants of the classical groups. Encyclopedia of Mathematics and its Applications, 68, Cambridge University Press, Cambridge, 1998. Google Scholar
[15] Grothendieck, A., Elements de geometrie algebrique. IV. Etude locale des schemas et des morphismes de schemas IV. Inst. Hautes Etudes Sci. Publ. Math. (1967), no. 32, 361. Google Scholar
[16] Harris, J., Algebraic geometry. Graduate Text in Mathematics, 133, Springer-Verlag, New York, 1992. http://dx.doi.org/10.1007/978-1-4757-2189-8 Google Scholar
[17] Hein, N., F. Sottile, and I. Zelenko, A congruence modulo four in real Schubert calculus. J. Reine Angew. Math. 714(2016), 151–174. http://dx.doi.org/10.1515/crelle-2013-0122 Google Scholar
[18] Hein, N., A congruence modulo four for real Schubert calculus with isotropic flags. Canad. Math. Bull., to appear. http://dx.doi.org/10.41 53/CMB-2O16-087-2 Google Scholar
[19] Helmke, U., J. Rosenthal, and Wang, X. A., Output feedback pole assignment for transfer functions with symmetries. SIAM J. Control Optim. 45(2006), no. 5,1898-1914. http://dx.doi.org/10.1137/050644276 Google Scholar
[20] Hillar, C. J. and F. Sottile, Complex static skew-symmetric output feedback control. SIAM J. Control Optim. 51(2013), no. 4, 3011–3026. http://dx.doi.org/10.1137/110855363 Google Scholar
[21] Martin, C. F. and R. Hermann, Applications of algebraic geometry to system theory: The McMillan degree andKronecker indices as topological and holomorphic invariants. SIAM J. Control Optim. 16(1978), no. 5, 743–755. http://dx.doi.org/10.1137/031 6050 Google Scholar
[22] Mukhin, E., V. Tarasov, and A. Varchenko, The B. and M. Shapiro conjecture in real algebraic geometry and the Bethe ansatz. Ann. of Math. (2) 170(2009), no. 2, 863–881. http://dx.doi.org/10.4007/annals.2009.1 70.863 Google Scholar
[23] Ovsienko, V. and S. Tabachnikov, Projective differential geometry old and new. Cambridge Tracts in Mathematics, 165, Cambridge University Press, Cambridge, 2005. Google Scholar
[24] Yu, V.. Ovsienko, Selfadjoint differential operators and curves on a Lagrangian Grassmannian that are subordinate to a loop. Mat. Zametki 47(1990), no. 3, 65–73,142; translation Math. Notes 47(1990), no. 3-4, 270-275. http://dx.doi.org/10.1007/BF01138507 Google Scholar
[25] Pankov, M., Geometry of semilinear embeddings. Relations to graphs and codes. World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2015. http://dx.doi.org/10.1142/9465 Google Scholar
[26] Schubert, H., Anzahl-Bestimmungen fur lineare Rdume beliebiger Dimension. Acta. Math. 8(1886), 97–118. http://dx.doi.org/10.1007/BF02417085 Google Scholar
[27] Shapiro, B. Z., Spaces of linear differential equations and flag manifolds. Izv. Akad. NaukSSSR Ser. Mat. 54(1990), no. 1,173-187, 223; translation in Math. USSR-Izv. 36(1991), no. 1,183-197. Google Scholar
[28] Shapiro, B. and M. Shapiro, Linear ordinary differential equations and Schubert calculus. Proceedings of the Gokova Geometry-Topology Conference 2010, Int. Press, 2011, pp. 79–87. Google Scholar
[29] Sottile, F., Frontiers of reality in Schubert Calculus. Bull. Amer. Math. Soc. 47(2010), no. 1, 31–71. http://dx.doi.org/10.1090/S0273-0979-09-01276-2 Google Scholar
[30] Wilczynski, E. J., Projective differential geometry. Bull. Amer. Math. Soc. 13(1906), no. 3,102-105. http://dx.doi.org/10.1090/S0002-9904-1906-01425-2 Google Scholar