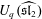2 results
YANG–BAXTER FIELD FOR SPIN HALL–LITTLEWOOD SYMMETRIC FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 October 2019, e39
-
- Article
-
- You have access
- Open access
- Export citation
-
Employing bijectivization of summation identities, we introduce local stochastic moves based on the Yang–Baxter equation for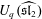
$U_{q}(\widehat{\mathfrak{sl}_{2}})$. Combining these moves leads to a new object which we call the spin Hall–Littlewood Yang–Baxter field—a probability distribution on two-dimensional arrays of particle configurations on the discrete line. We identify joint distributions along down-right paths in the Yang–Baxter field with spin Hall–Littlewood processes, a generalization of Schur processes. We consider various degenerations of the Yang–Baxter field leading to new dynamic versions of the stochastic six-vertex model and of the Asymmetric Simple Exclusion Process.
functional identities for the rogers dilogarithm associated to cluster $y$-systems
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 5 / October 2005
- Published online by Cambridge University Press:
- 23 September 2005, pp. 755-760
- Print publication:
- October 2005
-
- Article
- Export citation
