Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T00:05:19.290Z Has data issue: false hasContentIssue false
  • English
  • Français

YANG–BAXTER FIELD FOR SPIN HALL–LITTLEWOOD SYMMETRIC FUNCTIONS

Part of: Equilibrium statistical mechanics Special processes Combinatorial probability Algebraic combinatorics

Published online by Cambridge University Press:  31 October 2019

ALEXEY BUFETOV  and
LEONID PETROV
ALEXEY BUFETOV
Affiliation:
Massachusetts Institute of Technology, Department of Mathematics, 77 Massachusetts Avenue, Cambridge, MA 02139, USA; [email protected]
LEONID PETROV
Affiliation:
University of Virginia, Department of Mathematics, 141 Cabell Drive, Kerchof Hall, P.O. Box 400137, Charlottesville, VA 22904, USA Institute for Information Transmission Problems, Bolshoy Karetny per. 19, Moscow 127994, Russia; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Employing bijectivization of summation identities, we introduce local stochastic moves based on the Yang–Baxter equation for 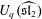$U_{q}(\widehat{\mathfrak{sl}_{2}})$. Combining these moves leads to a new object which we call the spin Hall–Littlewood Yang–Baxter field—a probability distribution on two-dimensional arrays of particle configurations on the discrete line. We identify joint distributions along down-right paths in the Yang–Baxter field with spin Hall–Littlewood processes, a generalization of Schur processes. We consider various degenerations of the Yang–Baxter field leading to new dynamic versions of the stochastic six-vertex model and of the Asymmetric Simple Exclusion Process.

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60C05: Combinatorial probability 05E05: Symmetric functions and generalizations 82B23: Exactly solvable models; Bethe ansatz
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e39
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Aggarwal, A., ‘Dynamical stochastic higher spin vertex models’, Selecta Math. 24(3) (2018), 2659–2735.Google Scholar
Aggarwal, A., Borodin, A. and Bufetov, A., ‘Stochasticization of solutions to the Yang-Baxter equation’, Ann. Henri Poincaré 20(8) (2019), 2495–2554.Google Scholar
Baik, J., Deift, P. and Johansson, K., ‘On the distribution of the length of the longest increasing subsequence of random permutations’, J. Amer. Math. Soc. 12(4) (1999), 1119–1178.Google Scholar
Baryshnikov, Y., ‘GUEs and queues’, Probab. Theory Related Fields 119 (2001), 256–274.Google Scholar
Baxter, R., Exactly Solved Models in Statistical Mechanics (Courier Dover Publications, Mineola, NY, 2007).Google Scholar
Betea, D., Boutillier, C., Bouttier, J., Chapuy, G., Corteel, S. and Vuletić, M., ‘Perfect sampling algorithm for Schur processes’, Markov Process. Related Fields 24(3) (2017), 381–418.Google Scholar
Betea, D. and Wheeler, M., ‘Refined Cauchy and Littlewood identities, plane partitions and symmetry classes of alternating sign matrices’, J. Combin. Theory Ser A 137 (2016), 126–165.Google Scholar
Betea, D., Wheeler, M. and Zinn-Justin, P., ‘Refined Cauchy/Littlewood identities and six-vertex model partition functions: II. Proofs and new conjectures’, J. Algebraic Combin. 42(2) (2015), 555–603.Google Scholar
Borodin, A., ‘Schur dynamics of the Schur processes’, Adv. Math. 228(4) (2011), 2268–2291.Google Scholar
Borodin, A., ‘Stochastic higher spin six vertex model and Macdonald measures’, J. Math. Phys. 59(2) (2018), 023301.Google Scholar
Borodin, A., ‘On a family of symmetric rational functions’, Adv. Math. 306 (2017), 973–1018.Google Scholar
Borodin, A., ‘Symmetric elliptic functions, IRF models, and dynamic exclusion processes’, Preprint, 2017, arXiv:1701.05239 [math-ph].Google Scholar
Borodin, A., Bufetov, A. and Wheeler, M., ‘Between the stochastic six vertex model and Hall–Littlewood processes’, Duke Math. J. 167(13) (2018), 2457–2529.Google Scholar
Borodin, A. and Corwin, I., ‘Macdonald processes’, Probab. Theory Related Fields 158 (2014), 225–400.Google Scholar
Borodin, A. and Corwin, I., ‘Discrete time q-TASEPs’, Int. Math. Res. Not. IMRN 2015(2) (2015), 499–537.Google Scholar
Borodin, A. and Corwin, I., ‘Dynamic ASEP, duality and continuous $q^{-1}$ -Hermite polynomials’, Preprint, 2017, arXiv:1705.01980 [math.PR].Google Scholar
Borodin, A., Corwin, I., Ferrari, P. and Veto, B., ‘Height fluctuations for the stationary KPZ equation’, Math. Phys. Anal. Geom. 18(1) (2015), 1–95.Google Scholar
Borodin, A., Corwin, I. and Gorin, V., ‘Stochastic six-vertex model’, Duke J. Math. 165(3) (2016), 563–624.Google Scholar
Borodin, A., Corwin, I., Gorin, V. and Shakirov, S., ‘Observables of Macdonald processes’, Trans. Amer. Math. Soc. 368(3) (2016), 1517–1558.Google Scholar
Borodin, A., Corwin, I., Petrov, L. and Sasamoto, T., ‘Spectral theory for interacting particle systems solvable by coordinate Bethe ansatz’, Commun. Math. Phys. 339(3) (2015), 1167–1245.Google Scholar
Borodin, A., Corwin, I., Petrov, L. and Sasamoto, T., ‘Spectral theory for the q-Boson particle system’, Compos. Math. 151(1) (2015), 1–67.Google Scholar
Borodin, A. and Ferrari, P., ‘Large time asymptotics of growth models on space-like paths I: PushASEP’, Electron. J. Probab. 13 (2008), 1380–1418.Google Scholar
Borodin, A. and Ferrari, P., ‘Anisotropic growth of random surfaces in 2 + 1 dimensions’, Commun. Math. Phys. 325 (2014), 603–684.Google Scholar
Borodin, A. and Gorin, V., ‘General 𝛽-Jacobi corners process and the Gaussian free field’, Comm. Pure Appl. Math. 68(10) (2015), 1774–1844.Google Scholar
Borodin, A. and Petrov, L., ‘Integrable probability: From representation theory to Macdonald processes’, Probab. Surv. 11 (2014), 1–58.Google Scholar
Borodin, A. and Petrov, L., ‘Nearest neighbor Markov dynamics on Macdonald processes’, Adv. Math. 300 (2016), 71–155.Google Scholar
Borodin, A. and Petrov, L., ‘Higher spin six vertex model and symmetric rational functions’, Selecta Math. 24(2) (2018), 751–874.Google Scholar
Borodin, A. and Petrov, L., ‘Inhomogeneous exponential jump model’, Probab. Theory Related Fields 172 (2018), 323–385.Google Scholar
Bufetov, A. and Matveev, K., ‘Hall–Littlewood RSK field’, Selecta Math. 24(5) (2018), 4839–4884.Google Scholar
Bufetov, A. and Petrov, L., ‘Law of large numbers for infinite random matrices over a finite field’, Selecta Math. 21(4) (2015), 1271–1338.Google Scholar
Corwin, I., ‘The Kardar–Parisi–Zhang equation and universality class’, Random Matrices Theory Appl. 1(1) (2012), 1130001.Google Scholar
Corwin, I., ‘Kardar–Parisi–Zhang universality’, Notices Amer. Math. Soc. 63(3) (2016), 230–239.Google Scholar
Corwin, I., O’Connell, N., Seppäläinen, T. and Zygouras, N., ‘Tropical combinatorics and Whittaker functions’, Duke J. Math. 163(3) (2014), 513–563.Google Scholar
Corwin, I. and Petrov, L., ‘The q-PushASEP: a new integrable model for traffic in 1 + 1 dimension’, J. Stat. Phys. 160(4) (2015), 1005–1026.Google Scholar
Corwin, I. and Petrov, L., ‘Stochastic higher spin vertex models on the line’, Comm. Math. Phys. 343(2) (2016), 651–700.Google Scholar
Diaconis, P. and Fill, J. A., ‘Strong stationary times via a new form of duality’, Ann. Probab. 18 (1990), 1483–1522.Google Scholar
Dimitrov, E., ‘KPZ and Airy limits of Hall–Littlewood random plane partitions’, Ann. Inst. Henri Poincaré Probab. Stat. 54(2) (2018), 640–693.Google Scholar
Derrida, B., Lebowitz, J., Speer, E. and Spohn, H., ‘Dynamics of an anchored Toom interface’, J. Phys. A 24(20) (1991), 4805–4834.Google Scholar
Ferrari, P., ‘The universal Airy1 and Airy2 processes in the totally asymmetric simple exclusion process’, inIntegrable Systems and Random Matrices: In Honor of Percy Deift, (eds. Baik, J., Kriecherbauer, T., Li, L.-C., McLaughlin, K. T.-R. and Tomei, C.) Contemporary Mathematics (American Mathematical Society, Providence, RI, 2008), 321–332.Google Scholar
Fomin, S., ‘Generalized Robinson-Schnested-Knuth correspondence’, Zap. Nauchn. Sem. (LOMI) 155 (1986), 156–175 (in Russian).Google Scholar
Fomin, S., ‘Schensted algorithms for dual graded graphs’, J. Algebraic Combin. 4(1) (1995), 5–45.Google Scholar
Gimmett, G. and Manolescu, I., ‘Bond percolation on isoradial graphs: criticality and universality’, Probab. Theory Related Fields 159(1–2) (2014), 273–327.Google Scholar
Gwa, L.-H. and Spohn, H., ‘Six-vertex model, roughened surfaces, and an asymmetric spin Hamiltonian’, Phys. Rev. Lett. 68(6) (1992), 725–728.Google Scholar
Halpin-Healy, T. and Takeuchi, K., ‘A KPZ cocktail-shaken, not stirred …’, J. Stat. Phys. 160(4) (2015), 794–814.Google Scholar
Johansson, K., ‘Shape fluctuations and random matrices’, Comm. Math. Phys. 209(2) (2000), 437–476.Google Scholar
Kirillov, A. N., ‘Introduction to tropical combinatorics’, inPhysics and Combinatorics, Proceedings of the Nagoya 2000 International Workshop (Singapore) (eds. Kirillov, A. N. and Liskova, N.) (World Scientific, Singapore, 2001), 82–150.Google Scholar
Kirillov, A. N. and Reshetikhin, N., ‘Exact solution of the integrable XXZ Heisenberg model with arbitrary spin. I. The ground state and the excitation spectrum’, J. Phys. A 20(6) (1987), 1565–1585.Google Scholar
Korepin, V., Bogoliubov, N. and Izergin, A., Quantum Inverse Scattering Method and Correlation Functions, (Cambridge University Press, Cambridge, 1993).Google Scholar
Kulish, P. and Reshetikhin, N., ‘Quantum linear problem for the Sine–Gordon equation and higher representations’, New York J. Math. Sci. 23 (1983), 2435–2441.Google Scholar
Kulish, P., Reshetikhin, N. and Sklyanin, E., ‘Yang–Baxter equation and representation theory: I’, Lett. Math. Phys. 5 (1981), 393–403.Google Scholar
Lieb, E. H., ‘Residual entropy of square ice’, Phys. Rev. 162(1) (1967), 162–172.Google Scholar
MacDonald, C., Gibbs, J. and Pipkin, A., ‘Kinetics of biopolymerization on nucleic acid templates’, Biopolymers 6(1) (1968), 1–25.Google Scholar
Macdonald, I. G., Symmetric Functions and Hall Polynomials, 2nd edn, (Oxford University Press, Oxford, UK, 1995).Google Scholar
Mangazeev, V., ‘On the Yang–Baxter equation for the six-vertex model’, Nuclear Phys. B 882 (2014), 70–96.Google Scholar
Matveev, K. and Petrov, L., ‘ q-randomized Robinson–Schensted–Knuth correspondences and random polymers’, Ann. Inst. Henri Poincare D 4(1) (2017), 1–123.Google Scholar
Noumi, M. and Yamada, Y., ‘Tropical Robinson–Schensted–Knuth correspondence and birational Weyl group actions’, inRepresentation Theory of Algebraic Groups and Quantum Groups, Adv. Stud. Pure Math., 40 (Math. Soc. Japan, Tokyo, 2004), 371–442.Google Scholar
O’Connell, N., ‘A path-transformation for random walks and the Robinson–Schensted correspondence’, Trans. Amer. Math. Soc. 355(9) (2003), 3669–3697.Google Scholar
O’Connell, N., ‘Conditioned random walks and the RSK correspondence’, J. Phys. A 36(12) (2003), 3049–3066.Google Scholar
O’Connell, N., ‘Directed polymers and the quantum Toda lattice’, Ann. Probab. 40(2) (2012), 437–458.Google Scholar
O’Connell, N. and Pei, Y., ‘A q-weighted version of the Robinson–Schensted algorithm’, Electron. J. Probab. 18(95) (2013), 1–25.Google Scholar
O’Connell, N., Seppäläinen, T. and Zygouras, N., ‘Geometric RSK correspondence, Whittaker functions and symmetrized random polymers’, Invent. Math. 197 (2014), 361–416.Google Scholar
O’Connell, N. and Yor, M., ‘A representation for non-colliding random walks’, Electron. Commun. Probab. 7 (2002), 1–12.Google Scholar
Okounkov, A., ‘Infinite wedge and random partitions’, Selecta Math. 7(1) (2001), 57–81.Google Scholar
Okounkov, A. and Reshetikhin, N., ‘Correlation function of Schur process with application to local geometry of a random 3-dimensional Young diagram’, J. Amer. Math. Soc. 16(3) (2003), 581–603.Google Scholar
Pauling, L., ‘The structure and entropy of ice and of other crystals with some randomness of atomic arrangement’, J. Amer. Chem. Soc. 57(12) (1935), 2680–2684.Google Scholar
Pei, Y., ‘A symmetry property for q-weighted Robinson–Schensted algorithms and other branching insertion algorithms’, J. Algebraic Combin. 40 (2013), 743–770.Google Scholar
Pei, Y., ‘A $q$ -Robinson–Schensted–Knuth Algorithm and a $q$ -polymer’, Preprint, 2016, arXiv:1610.03692 [math.CO].Google Scholar
Petrov, L., ‘PushTASEP in inhomogeneous space’, In preparation, 2020.Google Scholar
Povolotsky, A., ‘On integrability of zero-range chipping models with factorized steady state’, J. Phys. A 46 465205 (2013).Google Scholar
Prähofer, M. and Spohn, H., ‘Scale invariance of the PNG droplet and the Airy process’, J. Stat. Phys. 108 (2002), 1071–1106.Google Scholar
Seppäläinen, T., ‘Scaling for a one-dimensional directed polymer with boundary conditions’, Ann. Probab. 40(1) (2012), 19–73.Google Scholar
Spitzer, F., ‘Interaction of Markov processes’, Adv. Math. 5(2) (1970), 246–290.Google Scholar
Sportiello, A., Personal communication, 2015.Google Scholar
Tsilevich, N., ‘Quantum inverse scattering method for the q-boson model and symmetric functions’, Funct. Anal. Appl. 40(3) (2006), 207–217.Google Scholar
Vershik, A. and Kerov, S., ‘The characters of the infinite symmetric group and probability properties of the Robinson–Shensted–Knuth algorithm’, SIAM J. Algebra Discrete Math. 7(1) (1986), 116–124.Google Scholar
Warren, J. and Windridge, P., ‘Some examples of dynamics for Gelfand–Tsetlin patterns’, Electron. J. Probab. 14 (2009), 1745–1769.Google Scholar
Weyl, H., The Classical Groups. Their Invariants and Representations, (Princeton University Press, Princeton, NJ, 1997).Google Scholar
Wheeler, M. and Zinn-Justin, P., ‘Refined Cauchy/Littlewood identities and six-vertex model partition functions: III. Deformed bosons’, Adv. Math. 299 (2016), 543–600.Google Scholar
Yang, C. N., ‘Some exact results for the many-body problem in one dimension with repulsive delta-function interaction’, Phys. Rev. Lett. 19(23) (1967), 1312.Google Scholar