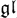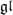Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (1)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

81r10 (17b10 81r12 34m35)

Glasgow Mathematical Journal (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

ON SEPARATION OF VARIABLES AND COMPLETENESS OF THE BETHE ANSATZ FOR QUANTUM N GAUDIN MODEL
E. MUKHIN, V. TARASOV, A. VARCHENKO
Journal:

Glasgow Mathematical Journal / Volume 51 / Issue A / February 2009

Published online by Cambridge University Press:

01 February 2009, pp. 137-145

Print publication:

February 2009
- Article
- - You have access
- PDF
- Export citation
In this paper, we discuss implications of the results obtained in [5]. It was shown there that eigenvectors of the Bethe algebra of the quantum 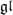N Gaudin model are in a one-to-one correspondence with Fuchsian differential operators with polynomial kernel. Here, we interpret this fact as a separation of variables in the 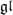N Gaudin model. Having a Fuchsian differential operator with polynomial kernel, we construct the corresponding eigenvector of the Bethe algebra. It was shown in [5] that the Bethe algebra has simple spectrum if the evaluation parameters of the Gaudin model are generic. In that case, our Bethe ansatz construction produces an eigenbasis of the Bethe algebra.