Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T20:07:55.918Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SEPARATION OF VARIABLES AND COMPLETENESS OF THE BETHE ANSATZ FOR QUANTUM N GAUDIN MODEL

Published online by Cambridge University Press:  01 February 2009

E. MUKHIN ,
V. TARASOV  and
A. VARCHENKO
E. MUKHIN
Affiliation:
Department of Mathematical Sciences, Indiana University – Purdue University Indianapolis402 North Blackford St, Indianapolis, IN 46202-3216, USA e-mail: [email protected]
V. TARASOV
Affiliation:
St. Petersburg Branch of Steklov Mathematical InstituteFontanka 27, St. Petersburg, 191023, Russia e-mail: [email protected]
A. VARCHENKO
Affiliation:
Department of Mathematics, University of North Carolina at Chapel HillChapel Hill, NC 27599-3250, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

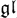
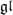In this paper, we discuss implications of the results obtained in [5]. It was shown there that eigenvectors of the Bethe algebra of the quantum N Gaudin model are in a one-to-one correspondence with Fuchsian differential operators with polynomial kernel. Here, we interpret this fact as a separation of variables in the 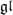N Gaudin model. Having a Fuchsian differential operator with polynomial kernel, we construct the corresponding eigenvector of the Bethe algebra. It was shown in [5] that the Bethe algebra has simple spectrum if the evaluation parameters of the Gaudin model are generic. In that case, our Bethe ansatz construction produces an eigenbasis of the Bethe algebra.

Keywords

81R10 (17B10 81R12 34M35)
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue A , February 2009 , pp. 137 - 145
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Babujian, H. M., Off-shell Bethe ansatz equation and N-point correlators in the SU(2) WZNW theory, J. Phys. A 26 (1993), 6981–6990.CrossRefGoogle Scholar
2.Mukhin, E., Tarasov, V. and Varchenko, A., The B. and M. Shapiro conjecture in real algebraic geometry and the Bethe ansatz, preprint math.AG/0512299.Google Scholar
3.Mukhin, E., Tarasov, V. and Varchenko, A., Bethe eigenvectors of higher transfer matrices, J. Stat. Mech. (8) (2006), P08002, 1–44.Google Scholar
4.Mukhin, E., Tarasov, V. and Varchenko, A., Generating operator of XXX or Gaudin transfer matrices has quasi-exponential kernel, SIGMA 6 (060) (2007), 1–31.Google Scholar
5.Mukhin, E., Tarasov, V. and Varchenko, A., Schubert calculus and representations of the general linear group, preprint, arXiv:0711.4079Google Scholar
6.Mukhin, E. and Varchenko, A., Multiple orthogonal polynomials and a counterexample to Gaudin Bethe Ansatz Conjecture, Trans. Amer. Math. Soc. 359 (11) (2007), 5383–5418.Google Scholar
7.Mukhin, E. and Varchenko, A., Norm of a Bethe vector and the Hessian of the master function, Compos. Math. 141 (4) (2005), 1012–1028.CrossRefGoogle Scholar
8.Reshetikhin, N. and Varchenko, A., Quasiclassical asymptotics of solutions to the KZ equations, Geometry, Topology and Physics, Conf. Proc. Lecture Notes Geom. Topology, IV, Int. Press, Cambridge, MA, 1995, 293–322, hep-th/9402126.Google Scholar
9.Schechtman, V. and Varchenko, A., Arrangements of hyperplanes and Lie algebra homology, Invent. Math. 106 (1991), 139–194.CrossRefGoogle Scholar
10.Sklyanin, E., Separation of variables in the Gaudin model, J. Sov. Math. 47 (2) (1989), 2473–2488.Google Scholar
11.Talalaev, D., Quantization of the Gaudin System, preprint, hep-th/0404153.Google Scholar