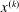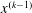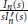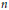7 results
MODELLING HUMAN CARRYING CAPACITY AS A FUNCTION OF FOOD AVAILABILITY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 3 / July 2020
- Published online by Cambridge University Press:
- 18 December 2020, pp. 318-333
-
- Article
- Export citation
Non-convex Optimization via Strongly Convex Majorization-minimization
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 726-737
- Print publication:
- December 2020
-
- Article
- Export citation
Estimation of a Regularisation Parameter for a Robin Inverse Problem
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 325-342
- Print publication:
- May 2017
-
- Article
- Export citation
BREAKING THE COHERENCE BARRIER: A NEW THEORY FOR COMPRESSED SENSING
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 15 February 2017, e4
-
- Article
-
- You have access
- Open access
- Export citation
Iterative Methods of Richardson-Lucy-Type for Image Deblurring
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 6 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 262-275
- Print publication:
- February 2013
-
- Article
- Export citation
A REVISED DUALITY PROOF OF SAMPLING LOCALIZATION IN RELAXATION SPECTRUM RECOVERY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 79-83
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
On the Singular Behavior of the Inverse Laplace Transforms of the Functions
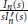 $\frac{{{I}_{n}}\left( s \right)}{sI_{n}^{\prime }\left( s \right)}$
$\frac{{{I}_{n}}\left( s \right)}{sI_{n}^{\prime }\left( s \right)}$
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 3 / 01 September 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 399-416
- Print publication:
- 01 September 2002
-
- Article
-
- You have access
- Export citation