On the Singular Behavior of the Inverse Laplace Transforms of the Functions 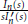$\frac{{{I}_{n}}\left( s \right)}{sI_{n}^{\prime }\left( s \right)}$

Abstract

Exact analytical expressions for the inverse Laplace transforms of the functions 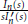$\frac{{{I}_{n}}\left( s \right)}{sI_{n}^{\prime }\left( s \right)}$ are obtained in the form of trigonometric series. The convergence of the series is analyzed theoretically, and it is proven that those diverge on an infinite denumerable set of points. Therefore it is shown that the inverse transforms have an infinite number of singular points. This result, to the best of the author’s knowledge, is new, as the inverse transforms of 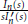$\frac{{{I}_{n}}\left( s \right)}{sI_{n}^{\prime }\left( s \right)}$ have previously been considered to be piecewise smooth and continuous. It is also found that the inverse transforms have an infinite number of points of finite discontinuity with different left- and right-side limits. The points of singularity and points of finite discontinuity alternate, and the sign of the infinity at the singular points also alternates depending on the order 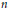$n$. The behavior of the inverse transforms in the proximity of the singular points and the points of finite discontinuity is addressed as well.