We show that normal and stable normal invariants of polarized homotopy equivalences of lens spaces  $M=\,L({{2}^{m}};\,{{r}_{1}},...,\,{{r}_{n}})$ and
$M=\,L({{2}^{m}};\,{{r}_{1}},...,\,{{r}_{n}})$ and  $N\,=\,L({{2}^{m}};\,{{s}_{1}},...,{{s}_{n}})$ are determined by certain
$N\,=\,L({{2}^{m}};\,{{s}_{1}},...,{{s}_{n}})$ are determined by certain  $\ell $-polynomials evaluated on the elementary symmetric functions
$\ell $-polynomials evaluated on the elementary symmetric functions  ${{\sigma }_{i}}\,(r_{1}^{2},...,r_{n}^{2})$ and
${{\sigma }_{i}}\,(r_{1}^{2},...,r_{n}^{2})$ and  ${{\sigma }_{i}}(s_{1}^{2},...,s_{n}^{2})$. Each polynomial
${{\sigma }_{i}}(s_{1}^{2},...,s_{n}^{2})$. Each polynomial  ${{\ell }_{k}}$ appears as the homogeneous part of degree
${{\ell }_{k}}$ appears as the homogeneous part of degree  $k$ in the Hirzebruch multiplicative
$k$ in the Hirzebruch multiplicative  $L$-sequence. When
$L$-sequence. When  $n=8$, the elementary symmetric functions alone determine the relevant normal invariants.
$n=8$, the elementary symmetric functions alone determine the relevant normal invariants.
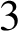 $3$
-MANIFOLDS IN
$3$
-MANIFOLDS IN
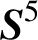 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$