Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T05:39:47.402Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal Thurston–Bennequin number and reducible Legendrian surgery

Part of: Low-dimensional topology Differential topology

Published online by Cambridge University Press:  30 June 2016

Kouichi Yasui
Kouichi Yasui*
Affiliation:
Department of Mathematics, Graduate School of Science, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, 739-8526, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a method for constructing a Legendrian representative of a knot in 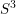$S^{3}$ which realizes its maximal Thurston–Bennequin number under a certain condition. The method utilizes Stein handle decompositions of 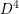$D^{4}$ , and the resulting Legendrian representative is often very complicated (relative to the complexity of the topological knot type). As an application, we construct infinitely many knots in 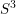$S^{3}$ each of which yields a reducible 3-manifold by a Legendrian surgery in the standard tight contact structure. This disproves a conjecture of Lidman and Sivek.

Keywords

4-manifoldLegendrian knotStein manifoldDehn surgerycabling conjecture

MSC classification

Primary: 57R17: Symplectic and contact topology 57R65: Surgery and handlebodies 57M25: Knots and links in $S^3$
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 9 , September 2016 , pp. 1899 - 1914
Copyright
© The Author 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akbulut, S. and Matveyev, R., Exotic structures and adjunction inequality , Turkish J. Math. 21 (1997), 47–53.Google Scholar
Eliashberg, Y., Topological characterization of Stein manifolds of dimension > 2 , Int. J. Math. 1 (1990), 29–46.CrossRefGoogle Scholar
Eliashberg, Y., Filling by holomorphic discs and its applications , in Geometry of low-dimensional manifolds, 2 (Durham, 1989), London Mathematical Society Lecture Note Series, vol. 151 (Cambridge University Press, Cambridge, 1990), 45–67.Google Scholar
Eliashberg, Y., Contact 3-manifolds twenty years since J. Martinet’s work , Ann. Inst. Fourier (Grenoble) 42 (1992), 165–192.CrossRefGoogle Scholar
Fintushel, R. and Stern, R. J., Immersed spheres in 4-manifolds and the immersed Thom conjecture , Turkish J. Math. 19 (1995), 145–157.Google Scholar
Fuchs, D. and Tabachnikov, S., Invariants of Legendrian and transverse knots in the standard contact space , Topology 36 (1997), 1025–1053.Google Scholar
Golla, M., Ozsváth–Szabó invariants of contact surgeries , Geom. Topol. 19 (2015), 171–235.Google Scholar
Gompf, R. E., Handlebody construction of Stein surfaces , Ann. of Math. (2) 148 (1998), 619–693.CrossRefGoogle Scholar
Gompf, R. E. and Stipsicz, A. I., 4-manifolds and Kirby calculus, Graduate Studies in Mathematics, vol. 20 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Gonzalez-Acuna, F. and Short, H., Knot surgery and primeness , Math. Proc. Cambridge Philos. Soc. 99 (1986), 89–102.Google Scholar
Gordon, C. McA. and Luecke, J., Only integral Dehn surgeries can yield reducible manifolds , Math. Proc. Cambridge Philos. Soc. 102 (1987), 97–101.CrossRefGoogle Scholar
Greene, J. E., L-space surgeries, genus bounds, and the cabling conjecture , J. Differential Geom. 100 (2015), 491–506.Google Scholar
Kronheimer, P. and Mrowka, T., The genus of embedded surfaces in the projective plane , Math. Res. Lett. 1 (1994), 797–808.Google Scholar
Lidman, T. and Sivek, S., Contact structures and reducible surgeries , Compos. Math. 152 (2016), 152–186.CrossRefGoogle Scholar
Lisca, P. and Matić, G., Tight contact structures and Seiberg–Witten invariants , Invent. Math. 129 (1997), 509–525.Google Scholar
Lisca, P. and Matić, G., Stein 4-manifolds with boundary and contact structures , Topology Appl. 88 (1998), 55–66.Google Scholar
Morgan, J., Szabó, Z. and Taubes, C., A product formula for the Seiberg–Witten invariants and the generalized Thom conjecture , J. Differential Geom. 44 (1996), 706–788.Google Scholar
Ng, L., A Legendrian Thurston–Bennequin bound from Khovanov homology , Algebr. Geom. Topol. 5 (2005), 1637–1653.Google Scholar
Ng, L., On arc index and maximal Thurston–Bennequin number , J. Knot Theory Ramifications 21 (2012), 1250031, 11 pp.Google Scholar
Ozbagci, B. and Stipsicz, A. I., Surgery on contact 3-manifolds and Stein surfaces, Bolyai Society Mathematical Studies, vol. 13 (Springer, Berlin, 2004), Janos Bolyai Mathematical Society, Budapest.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., The symplectic Thom conjecture , Ann. of Math. (2) 151 (2000), 93–124.CrossRefGoogle Scholar
Ozsvath, P. and Szabo, Z., Knot Floer homology and the four-ball genus , Geom. Topol. 7 (2003), 615–639.Google Scholar
Plamenevskaya, O., Bounds for the Thurston–Bennequin number from Floer homology , Algebr. Geom. Topol. 4 (2004), 399–406.Google Scholar
Plamenevskaya, O., Transverse knots and Khovanov homology , Math. Res. Lett. 13 (2006), 571–586.Google Scholar
Rasmussen, J., Khovanov homology and the slice genus , Invent. Math. 182 (2010), 419–447.Google Scholar
Shumakovitch, A., Rasmussen invariant, slice-Bennequin inequality, and sliceness of knots , J. Knot Theory Ramifications 16 (2007), 1403–1412.CrossRefGoogle Scholar
Yasui, K., Nonexistence of Stein structures on 4-manifolds and maximal Thurston–Bennequin numbers, J. Symplectic Geom., to appear. Preprint (2015), arXiv:1508.01491.Google Scholar