No CrossRef data available.
Published online by Cambridge University Press: 23 June 2023
We show that all large enough positive integral surgeries on algebraic knots bound a 4-manifold with a negative definite plumbing tree, which we describe explicitly. Then we apply the lattice embedding obstruction coming from Donaldson’s Theorem to classify the ones of the form 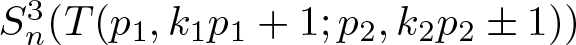 $S^3_n(T(p_1,k_1p_1+1; p_2, k_2p_2\pm 1))$ that also bound rational homology 4-balls.
$S^3_n(T(p_1,k_1p_1+1; p_2, k_2p_2\pm 1))$ that also bound rational homology 4-balls.