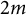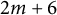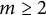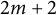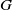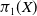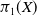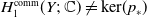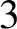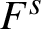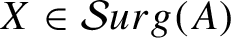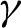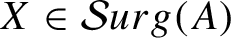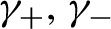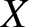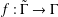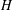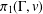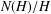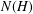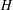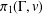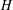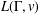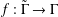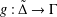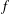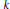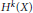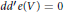10 results
Large N limit of the Yang–Mills measure on compact surfaces II: Makeenko–Migdal equations and the planar master field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 January 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poncelet’s closure theorem and the embedded topology of conic-line arrangements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 109-123
- Print publication:
- March 2025
-
- Article
- Export citation
Subrepresentations in the homology of finite covers of graphs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. 582-594
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anosov flows on
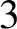 $3$
-manifolds: the surgeries and the foliations
$3$
-manifolds: the surgeries and the foliations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 27 April 2022, pp. 1129-1188
- Print publication:
- April 2023
-
- Article
- Export citation
Covering action on Conley index theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 21 February 2022, pp. 1633-1665
- Print publication:
- May 2023
-
- Article
- Export citation
GRAPH IMMERSIONS, INVERSE MONOIDS AND DECK TRANSFORMATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 02 March 2020, pp. 37-55
- Print publication:
- August 2021
-
- Article
- Export citation
Revisiting Leighton’s theorem with the Haar measure
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 615-623
- Print publication:
- May 2021
-
- Article
- Export citation
Virtual 1-domination of 3-manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 27 February 2018, pp. 621-639
- Print publication:
- March 2018
-
- Article
- Export citation
Cockcroft Properties of Thompson’s Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 3 / 01 September 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 268-281
- Print publication:
- 01 September 2000
-
- Article
-
- You have access
- Export citation
Embedding Coverings in Bundles
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 1 / 01 March 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 52-55
- Print publication:
- 01 March 1999
-
- Article
-
- You have access
- Export citation