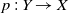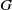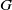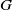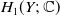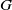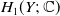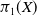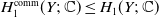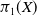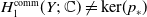1. Introduction
We study subrepresentations in the homology of finite covers of finite graphs, viewed as a representation of the deck group. The subrepresentations we consider arise from homology classes of lifts of closed curves that have interesting topological properties, for example, being primitive. One goal is to better understand the connection between topological properties of curves and representation-theoretic properties of their homology classes. For a finite, regular cover
![]() $p \;:\; Y \to X$
of finite graphs, with associated deck group
$p \;:\; Y \to X$
of finite graphs, with associated deck group
![]() $G$
, we know that
$G$
, we know that
![]() $H_1(Y;\;{\mathbb{C}}$
) is spanned by a finite set of closed loops. Let
$H_1(Y;\;{\mathbb{C}}$
) is spanned by a finite set of closed loops. Let
![]() $n$
be the rank of the free group
$n$
be the rank of the free group
![]() $\pi _1(X)$
. For a subset
$\pi _1(X)$
. For a subset
![]() $S \subseteq F_n = \pi _1(X)$
, we consider the subrepresentation:
$S \subseteq F_n = \pi _1(X)$
, we consider the subrepresentation:
where
![]() $\tilde{s}$
, called the preferred elevation of
$\tilde{s}$
, called the preferred elevation of
![]() $s$
, is the lift of the smallest power of
$s$
, is the lift of the smallest power of
![]() $s$
such that
$s$
such that
![]() $\tilde{s}$
is a closed loop in
$\tilde{s}$
is a closed loop in
![]() $Y$
, and
$Y$
, and
![]() $\left [ \tilde{s} \right ]$
its homology class. If
$\left [ \tilde{s} \right ]$
its homology class. If
![]() $S$
is the set of primitive elements in
$S$
is the set of primitive elements in
![]() $F_n$
, that is, loops in
$F_n$
, that is, loops in
![]() $X$
that are part of a basis of
$X$
that are part of a basis of
![]() $\pi _1(X)$
, we write
$\pi _1(X)$
, we write
![]() $H_1^{\textrm{prim}}(Y;\;{\mathbb{C}})$
for
$H_1^{\textrm{prim}}(Y;\;{\mathbb{C}})$
for
![]() $H_1^S(Y;\;{\mathbb{C}})$
and call this subrepresentation the primitive homology of
$H_1^S(Y;\;{\mathbb{C}})$
and call this subrepresentation the primitive homology of
![]() $Y$
, following Farb and Hensel [Reference Farb and Hensel3]. In this paper, the authors asked whether
$Y$
, following Farb and Hensel [Reference Farb and Hensel3]. In this paper, the authors asked whether
![]() $H_1^{\textrm{prim}}(Y;\;{\mathbb{C}})=H_1(Y;\;{\mathbb{C}})$
. This question was presumably first asked by Marché for the homology of surfaces with
$H_1^{\textrm{prim}}(Y;\;{\mathbb{C}})=H_1(Y;\;{\mathbb{C}})$
. This question was presumably first asked by Marché for the homology of surfaces with
![]() $\mathbb{Z}$
-coefficients, see [Reference Marché8], and later by Looijenga in [Reference Looijenga7]. Partial results were obtained by Farb and Hensel in [Reference Farb and Hensel3], where they showed that in fact equality holds for finite Abelian and
$\mathbb{Z}$
-coefficients, see [Reference Marché8], and later by Looijenga in [Reference Looijenga7]. Partial results were obtained by Farb and Hensel in [Reference Farb and Hensel3], where they showed that in fact equality holds for finite Abelian and
![]() $2$
-step nilpotent groups, the latter only when
$2$
-step nilpotent groups, the latter only when
![]() $n \geq 3$
; see [Reference Farb and Hensel3, Propositions 3.2 and 3.3]. Malestein and Putman gave a complete answer to this question in [Reference Malestein and Putman9, Theorem C, Example 1.3]. For every
$n \geq 3$
; see [Reference Farb and Hensel3, Propositions 3.2 and 3.3]. Malestein and Putman gave a complete answer to this question in [Reference Malestein and Putman9, Theorem C, Example 1.3]. For every
![]() $n \geq 2$
, they constructed a finite group which answers the question in the negative.
$n \geq 2$
, they constructed a finite group which answers the question in the negative.
A central role is played by the theorem of Gaschütz, see [Reference Chevalley, Weil and Hecke2] or [Reference Grunewald, Larsen, Lubotzky and Malestein5, Theorem 2.1], which identifies the first homology of
![]() $Y$
as a representation of
$Y$
as a representation of
![]() $G$
; namely, we have an isomorphism of
$G$
; namely, we have an isomorphism of
![]() $G$
-representations:
$G$
-representations:
where we denote by
![]() ${\mathbb{C}}_{\textrm{triv}}$
the trivial one-dimensional representation of
${\mathbb{C}}_{\textrm{triv}}$
the trivial one-dimensional representation of
![]() $G$
and by
$G$
and by
![]() ${\mathbb{C}}[G]$
the regular representation of
${\mathbb{C}}[G]$
the regular representation of
![]() $G$
.
$G$
.
To obstruct primitive homology from being all of homology, Farb and Hensel used the theorem of Gaschütz together with the following representation-theoretic property: if
![]() $l$
is a primitive loop in
$l$
is a primitive loop in
![]() $X$
, then the
$X$
, then the
![]() $G$
-orbit of the homology class of its preferred elevation is linearly independent, in other words
$G$
-orbit of the homology class of its preferred elevation is linearly independent, in other words
where
![]() $\phi \;:\; \pi _1(X) \to G$
is the epimorphism associated with the cover
$\phi \;:\; \pi _1(X) \to G$
is the epimorphism associated with the cover
![]() $p \;:\; Y \to X$
, compare [Reference Farb and Hensel3, Proposition 2.1]. From this, we obtain a necessary representation-theoretic condition for a homology class to be the homology class of a lift of a primitive element. Recall that a homology class in
$p \;:\; Y \to X$
, compare [Reference Farb and Hensel3, Proposition 2.1]. From this, we obtain a necessary representation-theoretic condition for a homology class to be the homology class of a lift of a primitive element. Recall that a homology class in
![]() $H_1(X;\;\mathbb{Z})$
can be represented by a primitive loop in
$H_1(X;\;\mathbb{Z})$
can be represented by a primitive loop in
![]() $X$
if and only if it is indivisible. The question arises whether there is a similar characterization for homology classes of lifts of primitive elements. Our first result shows that the necessary representation-theoretic property of Farb and Hensel is never sufficient for regular, Abelian covers.
$X$
if and only if it is indivisible. The question arises whether there is a similar characterization for homology classes of lifts of primitive elements. Our first result shows that the necessary representation-theoretic property of Farb and Hensel is never sufficient for regular, Abelian covers.
Theorem 1.1.
Let
![]() $G$
be the deck group of a finite, regular cover
$G$
be the deck group of a finite, regular cover
![]() $Y \to X$
of finite graphs with rank of
$Y \to X$
of finite graphs with rank of
![]() $\pi _1(X)$
at least 2. If
$\pi _1(X)$
at least 2. If
![]() $G$
is nontrivial Abelian, then there exists
$G$
is nontrivial Abelian, then there exists
![]() $z \in H_1(Y;\;\mathbb{Z})$
indivisible such that
$z \in H_1(Y;\;\mathbb{Z})$
indivisible such that
-
(i)
 $\textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}^G_{\langle g \rangle } ({\mathbb{C}}_{\textrm{triv}})$
for some
$\textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}^G_{\langle g \rangle } ({\mathbb{C}}_{\textrm{triv}})$
for some
 $g \in G$
, and
$g \in G$
, and
-
(ii)
 $z$
is not represented by an elevation of a primitive loop in
$z$
is not represented by an elevation of a primitive loop in
 $X$
.
$X$
.
We ask whether Theorem 1.1 also holds for non-Abelian groups.
We extend some of the above questions to other subsets
![]() $S \subseteq F_n$
. We consider the subset of primitive commutators, by which we mean a commutator of the form
$S \subseteq F_n$
. We consider the subset of primitive commutators, by which we mean a commutator of the form
![]() $[w, w']$
for
$[w, w']$
for
![]() $w, w'$
elements in a common basis of
$w, w'$
elements in a common basis of
![]() $F_n$
. Homology classes of elevations of primitive commutators satisfy the following representation-theoretic property, in analogy to [Reference Farb and Hensel3, Proposition 2.1] for primitive elements.
$F_n$
. Homology classes of elevations of primitive commutators satisfy the following representation-theoretic property, in analogy to [Reference Farb and Hensel3, Proposition 2.1] for primitive elements.
Proposition 1.2.
Let
![]() $G$
be the deck group of a finite, regular cover
$G$
be the deck group of a finite, regular cover
![]() $Y \to X$
of finite graphs with associated epimorphism
$Y \to X$
of finite graphs with associated epimorphism
![]() $\phi \;:\; \pi _1(X) \to G$
. Let
$\phi \;:\; \pi _1(X) \to G$
. Let
![]() $x_1$
,
$x_1$
,
![]() $x_2 \in F_n$
be two primitive elements that extend to a free basis of
$x_2 \in F_n$
be two primitive elements that extend to a free basis of
![]() $F_n$
. Set
$F_n$
. Set
![]() $x\;:\!=\; [x_1,x_2]$
, and let
$x\;:\!=\; [x_1,x_2]$
, and let
![]() $K \;:\!=\; \langle \phi (x) \rangle \leq \langle \phi (x_1), \phi (x_2) \rangle \;=\!:\; H \leq G$
be the subgroups of
$K \;:\!=\; \langle \phi (x) \rangle \leq \langle \phi (x_1), \phi (x_2) \rangle \;=\!:\; H \leq G$
be the subgroups of
![]() $G$
generated by
$G$
generated by
![]() $\phi (x)$
, respectively,
$\phi (x)$
, respectively,
![]() $\phi (x_1)$
and
$\phi (x_1)$
and
![]() $\phi (x_2)$
. Then we have the following isomorphism of
$\phi (x_2)$
. Then we have the following isomorphism of
![]() $G$
-representations:
$G$
-representations:
Note that if
![]() $K \leq H\leq G$
are subgroups, then
$K \leq H\leq G$
are subgroups, then
![]() $\textrm{Ind}_H^G({\mathbb{C}}_{\textrm{triv}})$
is a
$\textrm{Ind}_H^G({\mathbb{C}}_{\textrm{triv}})$
is a
![]() $G$
-subrepresentation of
$G$
-subrepresentation of
![]() $\textrm{Ind}_K^G({\mathbb{C}}_{\textrm{triv}})$
. Indeed, by transitivity of induction it suffices to realize that
$\textrm{Ind}_K^G({\mathbb{C}}_{\textrm{triv}})$
. Indeed, by transitivity of induction it suffices to realize that
![]() ${\mathbb{C}}_{\textrm{triv}}$
is an
${\mathbb{C}}_{\textrm{triv}}$
is an
![]() $H$
-subrepresentation of
$H$
-subrepresentation of
![]() $\textrm{Ind}_K^H({\mathbb{C}}_{\textrm{triv}})$
using for example Frobenius reciprocity; compare [Reference Serre10, Chapters 7.1–7.2].
$\textrm{Ind}_K^H({\mathbb{C}}_{\textrm{triv}})$
using for example Frobenius reciprocity; compare [Reference Serre10, Chapters 7.1–7.2].
Our next result shows that this representation-theoretic property is not sufficient in the case
![]() $n=2$
.
$n=2$
.
Proposition 1.3.
For
![]() $n=2$
there exists a finite, regular cover
$n=2$
there exists a finite, regular cover
![]() $p \;:\; Y \to X$
and
$p \;:\; Y \to X$
and
![]() $z \in H_1(Y;\;\mathbb{Z}) \cap \ker\!(p_*)$
indivisible, where
$z \in H_1(Y;\;\mathbb{Z}) \cap \ker\!(p_*)$
indivisible, where
![]() $p_*$
is the induced map on the associated homology groups, such that
$p_*$
is the induced map on the associated homology groups, such that
-
(i)
 $\textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}_{\langle g \rangle }^G({\mathbb{C}}_{\textrm{triv}})/{\mathbb{C}}_{\textrm{triv}}$
for some
$\textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}_{\langle g \rangle }^G({\mathbb{C}}_{\textrm{triv}})/{\mathbb{C}}_{\textrm{triv}}$
for some
 $g \in G$
, where
$g \in G$
, where
 $G$
is the deck group associated with the cover
$G$
is the deck group associated with the cover
 $p$
, and
$p$
, and
-
(ii)
 $z$
cannot be represented by an elevation of a primitive commutator in
$z$
cannot be represented by an elevation of a primitive commutator in
 $X$
.
$X$
.
We turn to the space
![]() $H_1^S(Y;\;{\mathbb{C}})$
for
$H_1^S(Y;\;{\mathbb{C}})$
for
![]() $S$
the subset of all primitive commutators over all bases of
$S$
the subset of all primitive commutators over all bases of
![]() $F_n$
(not just some fixed one) and write
$F_n$
(not just some fixed one) and write
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \leq H_1(Y;\;{\mathbb{C}})$
for this subrepresentation, the primitive commutator homology of
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \leq H_1(Y;\;{\mathbb{C}})$
for this subrepresentation, the primitive commutator homology of
![]() $Y$
. It is clear that
$Y$
. It is clear that
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \leq \ker\!(p_*) \neq H_1(Y;\;{\mathbb{C}})$
. One can ask whether
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \leq \ker\!(p_*) \neq H_1(Y;\;{\mathbb{C}})$
. One can ask whether
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) = \ker\!(p_*)$
holds.
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) = \ker\!(p_*)$
holds.
To obstruct primitive commutator homology to constitute all of
![]() $\ker\!(p_*)$
, we introduce the following notation as in [Reference Farb and Hensel3, Definition 1.3]. Let
$\ker\!(p_*)$
, we introduce the following notation as in [Reference Farb and Hensel3, Definition 1.3]. Let
![]() $\textrm{Irr}(G)$
be the set of representatives of the pairwise nonisomorphic irreducible
$\textrm{Irr}(G)$
be the set of representatives of the pairwise nonisomorphic irreducible
![]() $G$
-representations, and for
$G$
-representations, and for
![]() $S \subseteq F_n$
, let
$S \subseteq F_n$
, let
be the subset of those irreducible representations
![]() $V$
of
$V$
of
![]() $G$
that have the property that there is an element in
$G$
that have the property that there is an element in
![]() $S$
whose image has a nonzero fixed point. More precisely,
$S$
whose image has a nonzero fixed point. More precisely,
![]() $V \in \textrm{Irr}^S(\phi,G)$
if and only if there exists an element
$V \in \textrm{Irr}^S(\phi,G)$
if and only if there exists an element
![]() $s \in S$
and
$s \in S$
and
![]() $0 \neq v \in V$
such that
$0 \neq v \in V$
such that
![]() $\phi (s)(v)=v$
. If
$\phi (s)(v)=v$
. If
![]() $S$
is the set of primitive elements or primitive commutators, we write
$S$
is the set of primitive elements or primitive commutators, we write
![]() $\textrm{Irr}^{\textrm{prim}}(\phi,G)$
or
$\textrm{Irr}^{\textrm{prim}}(\phi,G)$
or
![]() $\textrm{Irr}^{\textrm{comm}}(\phi,G)$
, respectively. For a
$\textrm{Irr}^{\textrm{comm}}(\phi,G)$
, respectively. For a
![]() $G$
-representation
$G$
-representation
![]() $M$
and
$M$
and
![]() $V \in \textrm{Irr}(G)$
, we write
$V \in \textrm{Irr}(G)$
, we write
![]() $M(V)$
for the sum of all subrepresentations of
$M(V)$
for the sum of all subrepresentations of
![]() $M$
isomorphic to
$M$
isomorphic to
![]() $V$
and call them the homogeneous components of
$V$
and call them the homogeneous components of
![]() $M$
.
$M$
.
Theorem 1.4.
Let
![]() $G$
be the deck group of a finite, regular cover
$G$
be the deck group of a finite, regular cover
![]() $p \;:\; Y \to X$
of finite graphs with associated epimorphism
$p \;:\; Y \to X$
of finite graphs with associated epimorphism
![]() $\phi \;:\; \pi _1(X) \to G$
. Then,
$\phi \;:\; \pi _1(X) \to G$
. Then,
for
![]() $M=H_1(Y;\;{\mathbb{C}})$
.
$M=H_1(Y;\;{\mathbb{C}})$
.
The argument follows closely the one of [Reference Farb and Hensel3, Theorem 1.4]. The main ingredient of the proof of this theorem is Proposition 1.2. The theorem implies that whenever a group
![]() $G$
together with an epimorphism
$G$
together with an epimorphism
![]() $\phi \;:\; F_n \to G$
satisfies
$\phi \;:\; F_n \to G$
satisfies
![]() $\textrm{Irr}^{\textrm{comm}}(\phi,G) \neq \textrm{Irr}(G)$
, we conclude by the theorem of Gaschütz that
$\textrm{Irr}^{\textrm{comm}}(\phi,G) \neq \textrm{Irr}(G)$
, we conclude by the theorem of Gaschütz that
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \neq \ker\!(p_*)$
. We will give an example of a group with this property in the case
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \neq \ker\!(p_*)$
. We will give an example of a group with this property in the case
![]() $n=2$
. In fact, even more is true.
$n=2$
. In fact, even more is true.
Theorem 1.5.
For every
![]() $n \geq 2$
there exists a finite, regular cover
$n \geq 2$
there exists a finite, regular cover
![]() $p \;:\; Z \to X$
such that
$p \;:\; Z \to X$
such that
![]() $H_1^{\textrm{comm}}(Z;\;{\mathbb{C}}) \neq \ker\!(p_*)$
.
$H_1^{\textrm{comm}}(Z;\;{\mathbb{C}}) \neq \ker\!(p_*)$
.
The proof of this theorem relies on the result of Malestein and Putman on primitive homology; see [Reference Malestein and Putman9, Theorem C, Example 1.3].
Organization
The paper is organized as follows. Section 2 is solely concerned with homology classes of elevations of primitive elements. We will introduce the important results and finish by giving a proof of Theorem 1.1. In Section 3, we will prove a necessary representation-theoretic property of homology classes of elevations of primitive commutators (Proposition 1.2), but which is not sufficient to characterize those homology classes; see Proposition 1.3. In Section 4, we study the primitive commutator homology, and we will prove Theorem 1.4. We will discuss how primitive homology and primitive commutator homology relate, which will be essential in the proof of Theorem 1.5.
2. Homology classes of elevations of primitive elements
Let
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
![]() $n \geq 2$
, a finite group
$n \geq 2$
, a finite group
![]() $G$
and a surjective homomorphism
$G$
and a surjective homomorphism
![]() $\phi \;:\; F_n \to G$
, where
$\phi \;:\; F_n \to G$
, where
![]() $F_n = F \langle x_1, \ldots, x_n \rangle$
is the free group on
$F_n = F \langle x_1, \ldots, x_n \rangle$
is the free group on
![]() $n$
generators. Let
$n$
generators. Let
![]() $X$
be the wedge of
$X$
be the wedge of
![]() $n$
copies of
$n$
copies of
![]() $S^1$
with vertex
$S^1$
with vertex
![]() $x_0$
. Then we can associate with
$x_0$
. Then we can associate with
![]() $\phi$
a finite regular path-connected cover
$\phi$
a finite regular path-connected cover
![]() $p \;:\; Y \to X$
with base point
$p \;:\; Y \to X$
with base point
![]() $y_0 \in p^{-1}(x_0)$
and
$y_0 \in p^{-1}(x_0)$
and
![]() $p_*(\pi _1(Y,y_0))=\ker\!(\phi )$
. Under these assumptions, we have
$p_*(\pi _1(Y,y_0))=\ker\!(\phi )$
. Under these assumptions, we have
![]() $G \cong F_n/ \ker\!(\phi ) \cong \pi _1(X,x_0)/p_*(\pi _1(Y,y_0))$
and
$G \cong F_n/ \ker\!(\phi ) \cong \pi _1(X,x_0)/p_*(\pi _1(Y,y_0))$
and
![]() $G$
acts on
$G$
acts on
![]() $Y$
by graph automorphisms. This action extends to a linear action of
$Y$
by graph automorphisms. This action extends to a linear action of
![]() $G$
on the finite-dimensional
$G$
on the finite-dimensional
![]() $\mathbb{C}$
-vector space
$\mathbb{C}$
-vector space
![]() $H_1(Y;\;{\mathbb{C}})$
.
$H_1(Y;\;{\mathbb{C}})$
.
Recall that we call an element of a free (Abelian) group primitive if it is part of a free basis. An element of a free Abelian group is primitive if and only if it is indivisible, that means it cannot be written as a nontrivial multiple of some other element. Being indivisible is equivalent to the coefficient vector with respect to a basis having greatest common divisor one. A primitive element in
![]() $F_n$
has a primitive image under the quotient map to
$F_n$
has a primitive image under the quotient map to
![]() $\mathbb{Z}^n$
. On the other hand, every primitive element in
$\mathbb{Z}^n$
. On the other hand, every primitive element in
![]() $\mathbb{Z}^n$
has a primitive preimage in
$\mathbb{Z}^n$
has a primitive preimage in
![]() $F_n$
.
$F_n$
.
Definition 2.1.
For an element
![]() $l \in F_n$
, let
$l \in F_n$
, let
![]() $k(l)$
be the minimal number such that
$k(l)$
be the minimal number such that
![]() $l^{k(l)} \in \ker\!(\phi )$
. The preferred elevation
$l^{k(l)} \in \ker\!(\phi )$
. The preferred elevation
![]() $\tilde{l}$
of
$\tilde{l}$
of
![]() $l$
is the lift of
$l$
is the lift of
![]() $l^{k(l)}$
to
$l^{k(l)}$
to
![]() $Y$
at the base point
$Y$
at the base point
![]() $y_0$
. Lifts of
$y_0$
. Lifts of
![]() $l^{k(l)}$
at other preimages of
$l^{k(l)}$
at other preimages of
![]() $x_0$
are just called elevations. Unless clear from context we write
$x_0$
are just called elevations. Unless clear from context we write
![]() $\tilde{l}_p$
, where
$\tilde{l}_p$
, where
![]() $p \;:\; Y \to X$
is the covering map, to specify which cover we are lifting to.
$p \;:\; Y \to X$
is the covering map, to specify which cover we are lifting to.
Note that
![]() $k(l)$
is finite for all
$k(l)$
is finite for all
![]() $l \in F_n$
, since
$l \in F_n$
, since
![]() $G$
is finite. By the regularity of the cover, we obtain all elevations of
$G$
is finite. By the regularity of the cover, we obtain all elevations of
![]() $l$
by applying the elements of
$l$
by applying the elements of
![]() $G$
to the preferred elevation
$G$
to the preferred elevation
![]() $\tilde{l}$
. We can view
$\tilde{l}$
. We can view
![]() $\tilde{l}$
as an element in
$\tilde{l}$
as an element in
![]() $\pi _1(Y,y_0)$
, where it will also be called
$\pi _1(Y,y_0)$
, where it will also be called
![]() $\tilde{l}$
. Its homology class is denoted by square brackets
$\tilde{l}$
. Its homology class is denoted by square brackets
![]() $[\tilde{l}]$
. It is straightforward to verify that elevations of primitive elements are primitive.
$[\tilde{l}]$
. It is straightforward to verify that elevations of primitive elements are primitive.
For a cover
![]() $p \;:\; Y \to X$
we denote by
$p \;:\; Y \to X$
we denote by
![]() $p_*$
the induced morphisms on the level of fundamental groups and homology groups. Since
$p_*$
the induced morphisms on the level of fundamental groups and homology groups. Since
![]() $Y$
is finite, we have the transfer map
$Y$
is finite, we have the transfer map
![]() $p_{\#} \;:\; C_\bullet (X) \to C_\bullet (Y), \; x \mapsto \sum _{\tilde{x} \textrm{ lift of } x} \tilde{x}.$
The map
$p_{\#} \;:\; C_\bullet (X) \to C_\bullet (Y), \; x \mapsto \sum _{\tilde{x} \textrm{ lift of } x} \tilde{x}.$
The map
![]() $p_{\#}$
commutes with the differential operators and thus induces a map on homology, which will also be denoted by
$p_{\#}$
commutes with the differential operators and thus induces a map on homology, which will also be denoted by
![]() $p_{\#}$
. We have
$p_{\#}$
. We have
![]() $p_* \circ p_{\#} = |G| \cdot \textrm{id}$
, which in particular implies that
$p_* \circ p_{\#} = |G| \cdot \textrm{id}$
, which in particular implies that
![]() $p_* \;:\; H_1(Y;\;{\mathbb{C}})\to H_1(X;\;{\mathbb{C}})$
is surjective and
$p_* \;:\; H_1(Y;\;{\mathbb{C}})\to H_1(X;\;{\mathbb{C}})$
is surjective and
![]() $p_{\#} \;:\; H_1(X;\;{\mathbb{C}})\to H_1(Y;\;{\mathbb{C}})$
is injective.
$p_{\#} \;:\; H_1(X;\;{\mathbb{C}})\to H_1(Y;\;{\mathbb{C}})$
is injective.
For
![]() $l\in F_n$
, we observe that
$l\in F_n$
, we observe that
![]() $p_*([\tilde{l}]) = | \phi (l) | \cdot [ l ] \in H_1(X;\;\mathbb{Z})$
, since
$p_*([\tilde{l}]) = | \phi (l) | \cdot [ l ] \in H_1(X;\;\mathbb{Z})$
, since
![]() $k(l) = | \phi (l) |$
. If
$k(l) = | \phi (l) |$
. If
![]() $G$
is Abelian, and
$G$
is Abelian, and
![]() $\tilde{\phi } \;:\; \mathbb{Z}^n \to G$
denotes the homomorphism obtained from
$\tilde{\phi } \;:\; \mathbb{Z}^n \to G$
denotes the homomorphism obtained from
![]() $\phi$
which factors through
$\phi$
which factors through
![]() $\mathbb{Z}^n$
then
$\mathbb{Z}^n$
then
 \begin{equation} \phi (l) = \tilde{\phi }\!\left ([l]\right ) = \tilde{\phi } \!\left ( \frac{p_*([\tilde{l}])}{| \phi (l) |} \right ). \end{equation}
\begin{equation} \phi (l) = \tilde{\phi }\!\left ([l]\right ) = \tilde{\phi } \!\left ( \frac{p_*([\tilde{l}])}{| \phi (l) |} \right ). \end{equation}
We summarize the general setup of this article in the following diagram, which can be consulted at every point.

In the rest of this section, we will show that the property given in [Reference Farb and Hensel3, Proposition 2.1] is not sufficient to characterize elevations of primitive elements. We recall the statement here.
Proposition 2.2 (Farb–Hensel). Let
![]() $G$
be the deck group of a finite, regular cover
$G$
be the deck group of a finite, regular cover
![]() $p \;:\; Y \to X$
of finite graphs with associated epimorphism
$p \;:\; Y \to X$
of finite graphs with associated epimorphism
![]() $\phi \;:\; \pi _1(X) \to G$
. Let
$\phi \;:\; \pi _1(X) \to G$
. Let
![]() $l$
be a primitive loop in
$l$
be a primitive loop in
![]() $X$
and let
$X$
and let
![]() $\tilde{l}$
be its preferred elevation in
$\tilde{l}$
be its preferred elevation in
![]() $Y$
. We set
$Y$
. We set
![]() $z \;:\!=\; [\tilde{l}]$
and
$z \;:\!=\; [\tilde{l}]$
and
![]() $g \;:\!=\; \phi (l)$
. Then there is an isomorphism of
$g \;:\!=\; \phi (l)$
. Then there is an isomorphism of
![]() $G$
-representations:
$G$
-representations:
Note that this proposition contains two statements. First, it says that the
![]() $G$
-orbit of an elevation of a primitive element is
$G$
-orbit of an elevation of a primitive element is
![]() $\mathbb{C}$
-linearly independent. Secondly, it tells us that the subgroup over which we induce is related to the primitive element
$\mathbb{C}$
-linearly independent. Secondly, it tells us that the subgroup over which we induce is related to the primitive element
![]() $l$
we started with. It is cyclic and generated by
$l$
we started with. It is cyclic and generated by
![]() $\phi (l)$
. If
$\phi (l)$
. If
![]() $G$
is Abelian, this allows us to relate
$G$
is Abelian, this allows us to relate
![]() $z$
and
$z$
and
![]() $\phi (l)$
, see equation (2.1)—a fact which will be exploited in the proof of Theorem 1.1 to verify the insufficiency of this property.
$\phi (l)$
, see equation (2.1)—a fact which will be exploited in the proof of Theorem 1.1 to verify the insufficiency of this property.
Let
![]() $V_1={\mathbb{C}}_{\textrm{triv}}, \ldots, V_{k(G)}$
be representatives of the isomorphism classes of the irreducible
$V_1={\mathbb{C}}_{\textrm{triv}}, \ldots, V_{k(G)}$
be representatives of the isomorphism classes of the irreducible
![]() $G$
-representations, where
$G$
-representations, where
![]() $k(G)$
is the number of nonisomorphic irreducible
$k(G)$
is the number of nonisomorphic irreducible
![]() $G$
-representations. If
$G$
-representations. If
![]() $M$
is a
$M$
is a
![]() $G$
-representation, we write
$G$
-representation, we write
![]() $M(V_i)$
for the sum of all subrepresentations of
$M(V_i)$
for the sum of all subrepresentations of
![]() $M$
isomorphic to
$M$
isomorphic to
![]() $V_i$
and call them the homogeneous components of
$V_i$
and call them the homogeneous components of
![]() $M$
. Recall that if
$M$
. Recall that if
![]() $M={\mathbb{C}}[G]$
, then
$M={\mathbb{C}}[G]$
, then
![]() $M(V_i) \cong V_i^{\oplus \dim (V_i)}$
for all
$M(V_i) \cong V_i^{\oplus \dim (V_i)}$
for all
![]() $ 1 \leq i \leq k(G)$
, compare for example [Reference Isaacs6, Chapter 2]. The following lemma follows directly from the theorem of Gaschütz.
$ 1 \leq i \leq k(G)$
, compare for example [Reference Isaacs6, Chapter 2]. The following lemma follows directly from the theorem of Gaschütz.
Lemma 2.3.
Let
![]() $M=H_1(Y;\;{\mathbb{C}})$
. In the above setting, the following properties hold:
$M=H_1(Y;\;{\mathbb{C}})$
. In the above setting, the following properties hold:
-
(a)
 $p_{\#}(H_1(X;\;{\mathbb{C}})) \cong M(V_1)$
.
$p_{\#}(H_1(X;\;{\mathbb{C}})) \cong M(V_1)$
. -
(b)
 $\ker\!(p_*) \cong \bigoplus _{i=2}^{k(G)} M(V_i)$
.
$\ker\!(p_*) \cong \bigoplus _{i=2}^{k(G)} M(V_i)$
.
Together we obtain
![]() $H_1(Y;\;{\mathbb{C}}) = p_{\#}(H_1(X;\;{\mathbb{C}})) \oplus \ker\!(p_*)$
.
$H_1(Y;\;{\mathbb{C}}) = p_{\#}(H_1(X;\;{\mathbb{C}})) \oplus \ker\!(p_*)$
.
Proof.
-
(i) The group
 $G$
acts trivially on
$G$
acts trivially on
 $p_\#(H_1(X;\;{\mathbb{C}}))$
, since an element of the deck group permutes lifts. Hence,
$p_\#(H_1(X;\;{\mathbb{C}}))$
, since an element of the deck group permutes lifts. Hence,
 $p_{\#}(H_1(X;\;{\mathbb{C}})) \leq M(V_1)$
. Since
$p_{\#}(H_1(X;\;{\mathbb{C}})) \leq M(V_1)$
. Since
 $p_\#$
is injective as a map on homology, we obtain equality by the theorem of Gaschütz and dimensionality reasons.
$p_\#$
is injective as a map on homology, we obtain equality by the theorem of Gaschütz and dimensionality reasons. -
(ii) This follows from the theorem of Gaschütz and the fact that the map
 $p_* \;:\; H_1(Y;\;{\mathbb{C}}) \to H_1(X;\;{\mathbb{C}})$
is surjective. Indeed, we haveas
$p_* \;:\; H_1(Y;\;{\mathbb{C}}) \to H_1(X;\;{\mathbb{C}})$
is surjective. Indeed, we haveas \begin{equation*}M(V_1) \cong {\mathbb {C}}^n \cong H_1(X;\;{\mathbb {C}}) = \textrm {im}(p_*) \cong M/ \ker\!(p_*),\end{equation*}
\begin{equation*}M(V_1) \cong {\mathbb {C}}^n \cong H_1(X;\;{\mathbb {C}}) = \textrm {im}(p_*) \cong M/ \ker\!(p_*),\end{equation*}
 ${\mathbb{C}} [G]$
-modules, where
${\mathbb{C}} [G]$
-modules, where
 $G$
acts trivially on
$G$
acts trivially on
 $H_1(X;\;{\mathbb{C}})$
, so
$H_1(X;\;{\mathbb{C}})$
, so
 $\ker\!(p_*)$
does not have simple submodules isomorphic to
$\ker\!(p_*)$
does not have simple submodules isomorphic to
 $V_1$
. For dimensionality reasons, we obtain
$V_1$
. For dimensionality reasons, we obtain
 $\ker\!(p_*) \cong \bigoplus _{i=2}^{k(G)} M(V_i)$
.
$\ker\!(p_*) \cong \bigoplus _{i=2}^{k(G)} M(V_i)$
.
Let
![]() $x\in H_1(X;\;{\mathbb{C}})$
with
$x\in H_1(X;\;{\mathbb{C}})$
with
![]() $p_\#(x) \in \ker\!(p_*)$
. Then
$p_\#(x) \in \ker\!(p_*)$
. Then
![]() $p_*(p_\#(x))= |G|x =0$
, and hence
$p_*(p_\#(x))= |G|x =0$
, and hence
![]() $x=0$
. Thus,
$x=0$
. Thus,
![]() $\ker\!(p_*) \cap \textrm{im}( p_{\#}) = \{0\}$
.
$\ker\!(p_*) \cap \textrm{im}( p_{\#}) = \{0\}$
.
Before we prove our first result, we state the following lemma about induced representations.
Lemma 2.4.
Let
![]() $G$
be a finite group and
$G$
be a finite group and
![]() $M$
a representation of
$M$
a representation of
![]() $G$
over
$G$
over
![]() $\mathbb{C}$
. Assume there exists
$\mathbb{C}$
. Assume there exists
![]() $0 \neq m \in M$
such that
$0 \neq m \in M$
such that
![]() $Gm$
is linearly independent. Let
$Gm$
is linearly independent. Let
![]() $H \;:\!=\; \textrm{Stab}_G(m)$
. Then,
$H \;:\!=\; \textrm{Stab}_G(m)$
. Then,
Proof. Choose representatives
![]() $g_1 = 1, g_2, \ldots, g_{[G:H]}$
for the left cosets of
$g_1 = 1, g_2, \ldots, g_{[G:H]}$
for the left cosets of
![]() $H$
in
$H$
in
![]() $G$
. For all
$G$
. For all
![]() $g \in G$
,
$g \in G$
,
![]() $g$
can be uniquely written as
$g$
can be uniquely written as
![]() $g = g_i h$
for some
$g = g_i h$
for some
![]() $1 \leq i \leq [G \;:\; H]$
and
$1 \leq i \leq [G \;:\; H]$
and
![]() $h \in H$
. We then have
$h \in H$
. We then have
![]() $gm = g_i h m = g_i m$
, since
$gm = g_i h m = g_i m$
, since
![]() $h \in \textrm{Stab}_G(m)$
. Also note that if
$h \in \textrm{Stab}_G(m)$
. Also note that if
![]() $g_i m = g_j m$
, then
$g_i m = g_j m$
, then
![]() $g_j^{-1}g_i \in H$
, so
$g_j^{-1}g_i \in H$
, so
![]() $g_i \in g_jH$
which implies
$g_i \in g_jH$
which implies
![]() $i = j$
. Thus,
$i = j$
. Thus,
![]() $g_1 m, \ldots, g_{[G:H]}m$
is a basis for
$g_1 m, \ldots, g_{[G:H]}m$
is a basis for
![]() $\textrm{Span}_{{\mathbb{C}}[G]}\{m\}$
. By construction,
$\textrm{Span}_{{\mathbb{C}}[G]}\{m\}$
. By construction,
![]() $\textrm{Ind}^G_H({\mathbb{C}}_{\textrm{triv}}) = U_1 \oplus \ldots \oplus U_{[G:H]}$
as
$\textrm{Ind}^G_H({\mathbb{C}}_{\textrm{triv}}) = U_1 \oplus \ldots \oplus U_{[G:H]}$
as
![]() ${\mathbb{C}}[H]$
-modules with
${\mathbb{C}}[H]$
-modules with
![]() $U_1 ={\mathbb{C}}_{\textrm{triv}}$
as
$U_1 ={\mathbb{C}}_{\textrm{triv}}$
as
![]() ${\mathbb{C}}[H]$
-module, and
${\mathbb{C}}[H]$
-module, and
![]() $U_i = g_i U_1$
. Let
$U_i = g_i U_1$
. Let
![]() $u_1 \in U_1 \setminus \{0\}$
. Then
$u_1 \in U_1 \setminus \{0\}$
. Then
![]() $U_1 = \langle u_1\rangle$
and thus
$U_1 = \langle u_1\rangle$
and thus
![]() $U_i = \langle g_iu_1 \rangle$
for all
$U_i = \langle g_iu_1 \rangle$
for all
![]() $1 \leq i \leq [G \;:\; H]$
. Define
$1 \leq i \leq [G \;:\; H]$
. Define
![]() $\varphi \;:\; \textrm{Span}_{{\mathbb{C}}[G]}\{m\} \to \textrm{Ind}^G_H({\mathbb{C}}_{\textrm{triv}})$
,
$\varphi \;:\; \textrm{Span}_{{\mathbb{C}}[G]}\{m\} \to \textrm{Ind}^G_H({\mathbb{C}}_{\textrm{triv}})$
,
![]() $g_i m \mapsto g_i u_1$
, and
$g_i m \mapsto g_i u_1$
, and
![]() $\mathbb{C}$
-linear extension. This is an isomorphism of
$\mathbb{C}$
-linear extension. This is an isomorphism of
![]() ${\mathbb{C}}[G]$
-modules.
${\mathbb{C}}[G]$
-modules.
We are now ready to prove our first result.
Proof of Theorem 1.1. Recall that we would like to prove that if
![]() $G$
is the deck group of a finite, regular cover
$G$
is the deck group of a finite, regular cover
![]() $Y \to X$
of finite graphs with rank of
$Y \to X$
of finite graphs with rank of
![]() $\pi _1(X)$
at least two, and
$\pi _1(X)$
at least two, and
![]() $G$
is nontrivial Abelian, then there exists an indivisible homology class
$G$
is nontrivial Abelian, then there exists an indivisible homology class
![]() $z \in H_1(Y;\;\mathbb{Z})$
such that
$z \in H_1(Y;\;\mathbb{Z})$
such that
-
(i)
 $\textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}^G_{\langle g \rangle } ({\mathbb{C}}_{\textrm{triv}})$
for some
$\textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}^G_{\langle g \rangle } ({\mathbb{C}}_{\textrm{triv}})$
for some
 $g \in G$
, and
$g \in G$
, and -
(ii)
 $z$
is not represented by an elevation of a primitive loop in
$z$
is not represented by an elevation of a primitive loop in
 $X$
.
$X$
.
The proof has two parts: first, we construct an indivisible homology class
![]() $z \in H_1(Y;\;\mathbb{Z})$
starting from two homology classes of elevations of primitive elements. Second, we verify that
$z \in H_1(Y;\;\mathbb{Z})$
starting from two homology classes of elevations of primitive elements. Second, we verify that
![]() $z$
indeed satisfies conditions (i) and (ii).
$z$
indeed satisfies conditions (i) and (ii).
Claim. There are primitive loops
![]() $l', l''$
in
$l', l''$
in
![]() $X$
with
$X$
with
![]() $\langle \phi (l') \rangle \cap \langle \phi (l'') \rangle = \{1\}$
and
$\langle \phi (l') \rangle \cap \langle \phi (l'') \rangle = \{1\}$
and
![]() $\langle \phi (l') \rangle \neq \{1\}$
.
$\langle \phi (l') \rangle \neq \{1\}$
.
We will now prove the claim. Since
![]() $G$
is Abelian, the map
$G$
is Abelian, the map
![]() $\phi$
factors through
$\phi$
factors through
![]() $\mathbb{Z}^n$
, so we obtain a surjective homomorphism
$\mathbb{Z}^n$
, so we obtain a surjective homomorphism
![]() $\tilde{\phi } \;:\; \mathbb{Z}^n \to G$
of Abelian groups. By the invariant factor decomposition of finitely generated modules (refer e.g. to [Reference Bosch1, Chapter 2.9, Theorem 2]) the statement is clear for
$\tilde{\phi } \;:\; \mathbb{Z}^n \to G$
of Abelian groups. By the invariant factor decomposition of finitely generated modules (refer e.g. to [Reference Bosch1, Chapter 2.9, Theorem 2]) the statement is clear for
![]() $\tilde{\phi }$
because
$\tilde{\phi }$
because
![]() $G$
is nontrivial and
$G$
is nontrivial and
![]() $n\geq 2$
. Since the Abelianization
$n\geq 2$
. Since the Abelianization
![]() $F_n \to \mathbb{Z}^n$
has the property that every primitive element in
$F_n \to \mathbb{Z}^n$
has the property that every primitive element in
![]() $\mathbb{Z}^n$
has a primitive preimage, the claim is proven.
$\mathbb{Z}^n$
has a primitive preimage, the claim is proven.
Choose
![]() $l', l''$
primitive loops in
$l', l''$
primitive loops in
![]() $X$
that satisfy the above claim. To simplify notation, we set
$X$
that satisfy the above claim. To simplify notation, we set
![]() $g' \;:\!=\; \phi (l')$
and
$g' \;:\!=\; \phi (l')$
and
![]() $g'' \;:\!=\; \phi (l'') \in G$
. We consider the homology classes
$g'' \;:\!=\; \phi (l'') \in G$
. We consider the homology classes
![]() $z'=[\tilde{l'}]$
and
$z'=[\tilde{l'}]$
and
![]() $z''=[\tilde{l''}] \in H_1(Y;\;\mathbb{Z})$
of the preferred elevations
$z''=[\tilde{l''}] \in H_1(Y;\;\mathbb{Z})$
of the preferred elevations
![]() $\tilde{l'}$
and
$\tilde{l'}$
and
![]() $\tilde{l''}$
of the two primitive loops
$\tilde{l''}$
of the two primitive loops
![]() $l'$
and
$l'$
and
![]() $l''$
, respectively. The elements
$l''$
, respectively. The elements
![]() $z'$
and
$z'$
and
![]() $z''$
will be used to build our desired homology class
$z''$
will be used to build our desired homology class
![]() $z$
. Write
$z$
. Write
![]() $z' = z'_{\!\!1} + z'_{\!\!2}+ \ldots + z'_{\!\!|G|}$
and
$z' = z'_{\!\!1} + z'_{\!\!2}+ \ldots + z'_{\!\!|G|}$
and
![]() $z'' = z''_{\!\!\!1} + z''_{\!\!\!2}+ \ldots + z''_{\!\!\!|G|}$
for the decomposition into the homogeneous components, that is,
$z'' = z''_{\!\!\!1} + z''_{\!\!\!2}+ \ldots + z''_{\!\!\!|G|}$
for the decomposition into the homogeneous components, that is,
![]() $z'_{\!\!i}$
,
$z'_{\!\!i}$
,
![]() $z''_{\!\!\!i} \in M(V_i)$
for
$z''_{\!\!\!i} \in M(V_i)$
for
![]() $i \leq 1 \leq |G|$
. By the theorem of Gaschütz, we have
$i \leq 1 \leq |G|$
. By the theorem of Gaschütz, we have
![]() $z'_{\!\!1}, z''_{\!\!\!1} \in V_1^{\oplus n}$
and
$z'_{\!\!1}, z''_{\!\!\!1} \in V_1^{\oplus n}$
and
![]() $z'_{\!\!i}, z''_{\!\!\!i} \in V_i^{\oplus (n-1)}$
for
$z'_{\!\!i}, z''_{\!\!\!i} \in V_i^{\oplus (n-1)}$
for
![]() $2 \leq i \leq |G|$
.
$2 \leq i \leq |G|$
.
We claim that
![]() $z'_{\!\!1} \in H_1(Y;\;\mathbb{Q})$
. Indeed, by Lemma 2.3(a), we know that there exists
$z'_{\!\!1} \in H_1(Y;\;\mathbb{Q})$
. Indeed, by Lemma 2.3(a), we know that there exists
![]() $x \in H_1(X;\;{\mathbb{C}})$
such that
$x \in H_1(X;\;{\mathbb{C}})$
such that
![]() $z'_{\!\!1} = p_\#(x)$
, and
$z'_{\!\!1} = p_\#(x)$
, and
![]() $|G| \, x = p_* \circ p_\# (x) = p_* (z'_{\!\!1}) = p_*(z') \in H_1(X;\;\mathbb{Z})$
, using that
$|G| \, x = p_* \circ p_\# (x) = p_* (z'_{\!\!1}) = p_*(z') \in H_1(X;\;\mathbb{Z})$
, using that
![]() $z'_{\!\!2}, \ldots, z'_{\!\!|G|} \in \ker\!(p_*)$
; see (b) in the same lemma. Thus,
$z'_{\!\!2}, \ldots, z'_{\!\!|G|} \in \ker\!(p_*)$
; see (b) in the same lemma. Thus,
![]() $ |G| \, z'_{\!\!1} = p_\#( |G| \, x) \in H_1(Y;\;\mathbb{Z}).$
By the same argument
$ |G| \, z'_{\!\!1} = p_\#( |G| \, x) \in H_1(Y;\;\mathbb{Z}).$
By the same argument
![]() $z''_{\!\!\!1} \in H_1(Y;\;\mathbb{Q})$
.
$z''_{\!\!\!1} \in H_1(Y;\;\mathbb{Q})$
.
Define
![]() $b \;:\!=\; z''_{\!\!\!1} - z'_{\!\!1} \in V_1^{\oplus n}$
and set
$b \;:\!=\; z''_{\!\!\!1} - z'_{\!\!1} \in V_1^{\oplus n}$
and set
Let
![]() $q \in \mathbb{Q}$
such that
$q \in \mathbb{Q}$
such that
![]() $z \;:\!=\; q \hat{z} \in H_1(Y;\;\mathbb{Z})$
is indivisible. This will be our candidate homology class.
$z \;:\!=\; q \hat{z} \in H_1(Y;\;\mathbb{Z})$
is indivisible. This will be our candidate homology class.
We come to the second part of the proof. First, we verify that (i) holds for
![]() $z$
. For this we need to show that the projection of
$z$
. For this we need to show that the projection of
![]() $\hat{z}$
to
$\hat{z}$
to
![]() $M(V_1)$
, namely
$M(V_1)$
, namely
![]() $z''_{\!\!\!1}$
, is nontrivial. Assuming this, it is a straightforward computation that
$z''_{\!\!\!1}$
, is nontrivial. Assuming this, it is a straightforward computation that
![]() $\textrm{Stab}_G(\hat{z}) = \textrm{Stab}_G(z') = \langle g' \rangle$
, and that the
$\textrm{Stab}_G(\hat{z}) = \textrm{Stab}_G(z') = \langle g' \rangle$
, and that the
![]() $G$
-orbit of
$G$
-orbit of
![]() $\hat{z}$
is linearly independent over
$\hat{z}$
is linearly independent over
![]() $\mathbb{C}$
, since this is true for
$\mathbb{C}$
, since this is true for
![]() $z'$
. Now (i) follows from Lemma 2.4 with
$z'$
. Now (i) follows from Lemma 2.4 with
To show that
![]() $z''_{\!\!\!1} \neq 0$
, we will argue by contradiction. In fact, if
$z''_{\!\!\!1} \neq 0$
, we will argue by contradiction. In fact, if
![]() $z''_{\!\!\!1} = 0$
, Lemma 2.3(b) implies that
$z''_{\!\!\!1} = 0$
, Lemma 2.3(b) implies that
![]() $0=p_*(z''_{\!\!\!1})=p_*(z'')= |g'' | [l'']$
, where the last equality holds since
$0=p_*(z''_{\!\!\!1})=p_*(z'')= |g'' | [l'']$
, where the last equality holds since
![]() $z''$
is the homology class of the preferred elevation of
$z''$
is the homology class of the preferred elevation of
![]() $l''$
. Thus,
$l''$
. Thus,
![]() $[l'']=0$
which contradicts the fact that
$[l'']=0$
which contradicts the fact that
![]() $l''$
is primitive.
$l''$
is primitive.
To verify (ii), we clearly need that
![]() $b \neq 0$
because otherwise
$b \neq 0$
because otherwise
![]() $z=z'$
. Assume for a contradiction that
$z=z'$
. Assume for a contradiction that
![]() $b=0$
, or equivalently
$b=0$
, or equivalently
![]() $z'_{\!\!1}=z''_{\!\!\!1}$
. By Lemma 2.3(b), it follows that
$z'_{\!\!1}=z''_{\!\!\!1}$
. By Lemma 2.3(b), it follows that
![]() $p_*(z')=p_*(z'')$
, and thus
$p_*(z')=p_*(z'')$
, and thus
![]() $|g'| [l'] =| g'' | [l''] \in H_1(X;\;\mathbb{Z})$
. Since
$|g'| [l'] =| g'' | [l''] \in H_1(X;\;\mathbb{Z})$
. Since
![]() $[l']$
and
$[l']$
and
![]() $[l'']$
are indivisible integral homology classes, they are equal. As
$[l'']$
are indivisible integral homology classes, they are equal. As
![]() $G$
is Abelian, we have
$G$
is Abelian, we have
![]() $g' = \tilde{\phi }([l'])= \tilde{\phi }([l''])=g''$
by equation (2.1), which contradicts the choice of
$g' = \tilde{\phi }([l'])= \tilde{\phi }([l''])=g''$
by equation (2.1), which contradicts the choice of
![]() $l'$
and
$l'$
and
![]() $l''$
.
$l''$
.
Knowing that
![]() $b\neq 0$
, assume now toward a contradiction that
$b\neq 0$
, assume now toward a contradiction that
![]() $z$
is the homology class of an elevation of a primitive element
$z$
is the homology class of an elevation of a primitive element
![]() $l$
in
$l$
in
![]() $X$
. By Proposition 2.2, we have
$X$
. By Proposition 2.2, we have
![]() $ \textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}_{\langle \phi (l) \rangle }^G ({\mathbb{C}}_{\textrm{triv}} ).$
On the other hand, by equation (2.2), we have
$ \textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}_{\langle \phi (l) \rangle }^G ({\mathbb{C}}_{\textrm{triv}} ).$
On the other hand, by equation (2.2), we have
with
![]() $g \;:\!=\; \phi (l)$
. Now
$g \;:\!=\; \phi (l)$
. Now
![]() $G$
Abelian implies that
$G$
Abelian implies that
![]() $\langle g \rangle = \langle g' \rangle$
, since representations of finite groups over
$\langle g \rangle = \langle g' \rangle$
, since representations of finite groups over
![]() $\mathbb{C}$
are determined by their characters and there is an explicit formula for the character of an induced representation; compare [Reference Isaacs6, Chapter 5]. Further, we compute
$\mathbb{C}$
are determined by their characters and there is an explicit formula for the character of an induced representation; compare [Reference Isaacs6, Chapter 5]. Further, we compute
Again by the indivisibility of the integral homology classes
![]() $[l]$
and
$[l]$
and
![]() $[l'']$
, we conclude that they are equal. Since
$[l'']$
, we conclude that they are equal. Since
![]() $G$
is Abelian, we obtain
$G$
is Abelian, we obtain
![]() $g = g''$
again by equation (2.1). This contradicts the fact that
$g = g''$
again by equation (2.1). This contradicts the fact that
![]() $\langle g' \rangle \cap \langle g'' \rangle = \{1\}$
and
$\langle g' \rangle \cap \langle g'' \rangle = \{1\}$
and
![]() $\langle g' \rangle \neq \{1\}$
.
$\langle g' \rangle \neq \{1\}$
.
In fact, a slightly stronger result can be verified using the same techniques as in the proof of the above proposition.
Corollary 2.5.
Let
![]() $z \in H_1(Y;\;\mathbb{Z})$
be the element constructed in the proof of Theorem 1.1. Then there is no element in
$z \in H_1(Y;\;\mathbb{Z})$
be the element constructed in the proof of Theorem 1.1. Then there is no element in
![]() $\textrm{Span}_{{\mathbb{C}} [G]} \{z\}$
which is the homology class of an elevation of a primitive loop in
$\textrm{Span}_{{\mathbb{C}} [G]} \{z\}$
which is the homology class of an elevation of a primitive loop in
![]() $X$
.
$X$
.
Proof. Assume there exists
![]() $z^* \in \textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cap H_1(Y;\;\mathbb{Z})$
indivisible with
$z^* \in \textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cap H_1(Y;\;\mathbb{Z})$
indivisible with
![]() $[ \tilde{l^*} ] = z^*$
for
$[ \tilde{l^*} ] = z^*$
for
![]() $l^* \in F_n$
primitive. Then
$l^* \in F_n$
primitive. Then
![]() $\textrm{Span}_{{\mathbb{C}} [G]} \{z^*\} \cong \textrm{Ind}_{\langle g^* \rangle }^G({\mathbb{C}}_{\textrm{triv}})$
with
$\textrm{Span}_{{\mathbb{C}} [G]} \{z^*\} \cong \textrm{Ind}_{\langle g^* \rangle }^G({\mathbb{C}}_{\textrm{triv}})$
with
![]() $g^*\;:\!=\; \phi (l^*) \in G$
by Proposition 2.2. We also have there exist
$g^*\;:\!=\; \phi (l^*) \in G$
by Proposition 2.2. We also have there exist
![]() $\alpha _1, \ldots, \alpha _{|G|} \in{\mathbb{C}}$
such that
$\alpha _1, \ldots, \alpha _{|G|} \in{\mathbb{C}}$
such that
![]() $z^* = \sum _{i=1}^{|G|} \alpha _i g_i z$
for
$z^* = \sum _{i=1}^{|G|} \alpha _i g_i z$
for
![]() $g_i \in G$
. Thus,
$g_i \in G$
. Thus,
 \begin{equation*}p_*(z^*) = \sum _{i=1}^{|G|} \alpha _i p_*(g_i z) = \underbrace { \left ( \sum _{i=1}^{|G|} \alpha _i \right ) }_{:= A} p_*(z), \end{equation*}
\begin{equation*}p_*(z^*) = \sum _{i=1}^{|G|} \alpha _i p_*(g_i z) = \underbrace { \left ( \sum _{i=1}^{|G|} \alpha _i \right ) }_{:= A} p_*(z), \end{equation*}
since
![]() $G$
acts as homeomorphisms of the covering space which preserve the projection map
$G$
acts as homeomorphisms of the covering space which preserve the projection map
![]() $p$
. Then
$p$
. Then
![]() $A \in \mathbb{Q}$
since both
$A \in \mathbb{Q}$
since both
![]() $p_*(z^*)$
,
$p_*(z^*)$
,
![]() $p_*(z)$
are in
$p_*(z)$
are in
![]() $H_1(X;\;\mathbb{Z})$
. Putting everything together, we obtain
$H_1(X;\;\mathbb{Z})$
. Putting everything together, we obtain
Since both
![]() $[l^*]$
and
$[l^*]$
and
![]() $[l'']$
are integral indivisible homology classes, they are equal, and thus
$[l'']$
are integral indivisible homology classes, they are equal, and thus
![]() $g^* = g''$
again by equation (2.1). Recall that
$g^* = g''$
again by equation (2.1). Recall that
![]() $\textrm{Stab}_G(z)=\langle g' \rangle$
. We claim that
$\textrm{Stab}_G(z)=\langle g' \rangle$
. We claim that
![]() $G$
Abelian implies that
$G$
Abelian implies that
![]() $\textrm{Stab}_G(z) \leq \textrm{Stab}_G(z^*)$
and
$\textrm{Stab}_G(z) \leq \textrm{Stab}_G(z^*)$
and
![]() $\textrm{Stab}_G(z^*) = \langle g^* \rangle$
. Indeed for
$\textrm{Stab}_G(z^*) = \langle g^* \rangle$
. Indeed for
![]() $g \in \textrm{Stab}_G(z)$
, we have
$g \in \textrm{Stab}_G(z)$
, we have
which proves the first part of the claim. For the second part of the claim, we observe that if
![]() $v_1,\ldots,v_{[G:\langle g^* \rangle ]}$
is a
$v_1,\ldots,v_{[G:\langle g^* \rangle ]}$
is a
![]() $\mathbb{C}$
-basis for
$\mathbb{C}$
-basis for
![]() $\textrm{Span}_{{\mathbb{C}} [G]} \{z^*\} \cong \textrm{Ind}_{\langle g^* \rangle }^G({\mathbb{C}}_{\textrm{triv}})$
which gets permuted transitively by
$\textrm{Span}_{{\mathbb{C}} [G]} \{z^*\} \cong \textrm{Ind}_{\langle g^* \rangle }^G({\mathbb{C}}_{\textrm{triv}})$
which gets permuted transitively by
![]() $G$
and for which
$G$
and for which
![]() $\textrm{Stab}_G(v_1)=\langle g^* \rangle$
, then
$\textrm{Stab}_G(v_1)=\langle g^* \rangle$
, then
![]() $\textrm{Stab}_G(v_k) = \langle g^* \rangle$
for all
$\textrm{Stab}_G(v_k) = \langle g^* \rangle$
for all
![]() $k=2,\ldots, [G\;:\;\langle g^* \rangle ]$
, and hence
$k=2,\ldots, [G\;:\;\langle g^* \rangle ]$
, and hence
![]() $\textrm{Stab}_G(z^*) \leq \langle g^* \rangle$
. By a dimension argument, we obtain equality. Thus, we obtain that
$\textrm{Stab}_G(z^*) \leq \langle g^* \rangle$
. By a dimension argument, we obtain equality. Thus, we obtain that
![]() $\langle g' \rangle = \textrm{Stab}_G(z) \leq \textrm{Stab}_G(z^*) = \langle g^* \rangle = \langle g'' \rangle$
, which contradicts the choice of
$\langle g' \rangle = \textrm{Stab}_G(z) \leq \textrm{Stab}_G(z^*) = \langle g^* \rangle = \langle g'' \rangle$
, which contradicts the choice of
![]() $l'$
and
$l'$
and
![]() $l''$
in the proof of Theorem 1.1.
$l''$
in the proof of Theorem 1.1.
3. Homology classes of elevations of primitive commutators
We begin this section by giving a proof of Proposition 1.2, which gives a necessary representation-theoretic property of homology classes of elevations of primitive commutators.
Proof of Proposition 1.2. Recall that we would like to prove that if
![]() $x_1$
and
$x_1$
and
![]() $x_2$
extend to a free basis of
$x_2$
extend to a free basis of
![]() $F_n$
and
$F_n$
and
![]() $x_{12} \;:\!=\; [x_1, x_2]$
, then
$x_{12} \;:\!=\; [x_1, x_2]$
, then
where
![]() $K \;:\!=\; \langle \phi (x_{12}) \rangle \leq \langle \phi (x_1), \phi (x_2) \rangle \;=\!:\; H \leq G$
.
$K \;:\!=\; \langle \phi (x_{12}) \rangle \leq \langle \phi (x_1), \phi (x_2) \rangle \;=\!:\; H \leq G$
.
Choose a base point preserving homotopy equivalence from
![]() $X$
to the wedge of
$X$
to the wedge of
![]() $n$
circles that maps
$n$
circles that maps
![]() $x_1$
and
$x_1$
and
![]() $x_2$
to two of the circles. Then there exists a unique (up to base point preserving homeomorphism that commutes with the covering map) finite regular cover of the wedge of
$x_2$
to two of the circles. Then there exists a unique (up to base point preserving homeomorphism that commutes with the covering map) finite regular cover of the wedge of
![]() $n$
circles such that the homotopy equivalence lifts to a homotopy equivalence of the corresponding covers and preserves base points. Since homotopy equivalences induce isomorphisms on the level of fundamental and homology groups, we can without loss of generality assume that
$n$
circles such that the homotopy equivalence lifts to a homotopy equivalence of the corresponding covers and preserves base points. Since homotopy equivalences induce isomorphisms on the level of fundamental and homology groups, we can without loss of generality assume that
![]() $X$
is a wedge of
$X$
is a wedge of
![]() $n$
circles,
$n$
circles,
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are two of those circles and that Y is a cover of this space.
$x_2$
are two of those circles and that Y is a cover of this space.
The proof now consists of two parts. First, we reduce to the case
![]() $n=2$
, where the statement simplifies to
$n=2$
, where the statement simplifies to
since
![]() $H=G$
. Second, we use surface topology to prove the claim in this special case. We start by reducing to the case
$H=G$
. Second, we use surface topology to prove the claim in this special case. We start by reducing to the case
![]() $n=2$
.
$n=2$
.
Let
![]() $X_1$
be the union of the two circles
$X_1$
be the union of the two circles
![]() $x_1$
and
$x_1$
and
![]() $x_2$
. Define
$x_2$
. Define
![]() $Y_1$
as the component of
$Y_1$
as the component of
![]() $p^{-1}(X_1)$
that contains the base point
$p^{-1}(X_1)$
that contains the base point
![]() $y_0$
. Now choose representatives for the left cosets of
$y_0$
. Now choose representatives for the left cosets of
![]() $H$
in
$H$
in
![]() $G$
, say
$G$
, say
![]() $g_1=1, \ldots, g_{[G:H]}$
and set
$g_1=1, \ldots, g_{[G:H]}$
and set
![]() $Y_i \;:\!=\; g_i Y_1$
for
$Y_i \;:\!=\; g_i Y_1$
for
![]() $1 \leq i \leq [G\;:\;H]$
. These are pairwise disjoint subgraphs of
$1 \leq i \leq [G\;:\;H]$
. These are pairwise disjoint subgraphs of
![]() $Y$
, since the vertices of
$Y$
, since the vertices of
![]() $Y$
correspond to the group elements and every group element is contained in exactly one
$Y$
correspond to the group elements and every group element is contained in exactly one
![]() $Y_i$
. It is easy to see that
$Y_i$
. It is easy to see that
![]() $I \;:\; \bigoplus _{i=1}^{[G:H]} H_1(Y_i;\;{\mathbb{C}}) \hookrightarrow H_1(Y;\;{\mathbb{C}})$
is injective, where
$I \;:\; \bigoplus _{i=1}^{[G:H]} H_1(Y_i;\;{\mathbb{C}}) \hookrightarrow H_1(Y;\;{\mathbb{C}})$
is injective, where
![]() $I$
is induced by the inclusions of the subgraphs into
$I$
is induced by the inclusions of the subgraphs into
![]() $Y$
; see for example [Reference Farb and Hensel4, Claim 2.4]. Note that
$Y$
; see for example [Reference Farb and Hensel4, Claim 2.4]. Note that
![]() $I$
is a morphism of
$I$
is a morphism of
![]() $G$
-representations, since the action of
$G$
-representations, since the action of
![]() $G$
on the direct sum is given by permuting the summands according to the permutation of the subgraphs
$G$
on the direct sum is given by permuting the summands according to the permutation of the subgraphs
![]() $Y_i$
. Now set
$Y_i$
. Now set
![]() $v \;:\!=\; [ \tilde{x}_{12} ]$
. By definition of
$v \;:\!=\; [ \tilde{x}_{12} ]$
. By definition of
![]() $Y_1$
, we have
$Y_1$
, we have
![]() $v \in H_1(Y_1;\;{\mathbb{C}})$
and, for every
$v \in H_1(Y_1;\;{\mathbb{C}})$
and, for every
![]() $h \in H$
, we have
$h \in H$
, we have
![]() $hv \in H_1(Y_1;\;{\mathbb{C}})$
. For
$hv \in H_1(Y_1;\;{\mathbb{C}})$
. For
![]() $g \in G$
write
$g \in G$
write
![]() $g = g_j h$
for some
$g = g_j h$
for some
![]() $1\leq j \leq [G\;:\;H]$
and
$1\leq j \leq [G\;:\;H]$
and
![]() $h \in H$
. Thus,
$h \in H$
. Thus,
![]() $g v = g_j h v \in H_1(g_j Y_1;\;{\mathbb{C}}) = H_1(Y_j;\;{\mathbb{C}})$
. We know that
$g v = g_j h v \in H_1(g_j Y_1;\;{\mathbb{C}}) = H_1(Y_j;\;{\mathbb{C}})$
. We know that
![]() $ \textrm{Span}_{{\mathbb{C}} [G] } \{v\} = \sum _{i=1}^{[G:H]} g_i \, \textrm{Span}_{{\mathbb{C}} [H]}\{v\},$
and, since
$ \textrm{Span}_{{\mathbb{C}} [G] } \{v\} = \sum _{i=1}^{[G:H]} g_i \, \textrm{Span}_{{\mathbb{C}} [H]}\{v\},$
and, since
![]() $I$
is injective, we conclude that this sum is in fact direct. Hence,
$I$
is injective, we conclude that this sum is in fact direct. Hence,
Proposition 1.2 in the case
![]() $n=2$
applies to
$n=2$
applies to
![]() $H$
since it is generated by two elements, and we obtain that
$H$
since it is generated by two elements, and we obtain that
![]() $\textrm{Span}_{{\mathbb{C}} [H]}\{v\} \cong \textrm{Ind}_K^H({\mathbb{C}}_{\textrm{triv}})/{\mathbb{C}}_{\textrm{triv}}$
. By the exactness of induction (see e.g. [Reference Serre10, Chapter 7.1]), it then follows that
$\textrm{Span}_{{\mathbb{C}} [H]}\{v\} \cong \textrm{Ind}_K^H({\mathbb{C}}_{\textrm{triv}})/{\mathbb{C}}_{\textrm{triv}}$
. By the exactness of induction (see e.g. [Reference Serre10, Chapter 7.1]), it then follows that
Thus, without loss of generality, we can assume that
![]() $n=2$
and
$n=2$
and
![]() $G=H$
. To prove the proposition in this case, we use surface topology. We would like to show that
$G=H$
. To prove the proposition in this case, we use surface topology. We would like to show that
![]() $ \textrm{Span}_{{\mathbb{C}} [G]} \{[\tilde{x}_{12}] \} \cong \textrm{Ind}_K^G({\mathbb{C}}_{\textrm{triv}})/{\mathbb{C}}_{\textrm{triv}}$
. We identify
$ \textrm{Span}_{{\mathbb{C}} [G]} \{[\tilde{x}_{12}] \} \cong \textrm{Ind}_K^G({\mathbb{C}}_{\textrm{triv}})/{\mathbb{C}}_{\textrm{triv}}$
. We identify
![]() $F_2$
with the fundamental group of the torus with one boundary component
$F_2$
with the fundamental group of the torus with one boundary component
![]() $T$
and base point
$T$
and base point
![]() $t_0 \in \partial T$
, with generators
$t_0 \in \partial T$
, with generators
![]() $x_1$
and
$x_1$
and
![]() $x_2$
represented by the simple closed curves as in the image below.
$x_2$
represented by the simple closed curves as in the image below.

Then,
![]() $x \;:\!=\; x_{12} = [x_1, x_2]$
is represented by
$x \;:\!=\; x_{12} = [x_1, x_2]$
is represented by
![]() $\alpha =\partial T$
. We have a group homomorphism
$\alpha =\partial T$
. We have a group homomorphism
![]() $\phi \;:\; \pi _1(T)\cong F_2 \to G$
, and we can associate with
$\phi \;:\; \pi _1(T)\cong F_2 \to G$
, and we can associate with
![]() $\ker\!(\phi )$
a finite, regular, path-connected cover
$\ker\!(\phi )$
a finite, regular, path-connected cover
![]() $q \;:\; S \to T$
with base point
$q \;:\; S \to T$
with base point
![]() $s_0 \in q^{-1}(t_0)$
and
$s_0 \in q^{-1}(t_0)$
and
![]() $q_*(\pi _1(S,s_0))=\ker\!(\phi )$
. Note that
$q_*(\pi _1(S,s_0))=\ker\!(\phi )$
. Note that
![]() $S$
is again an orientable surface with
$S$
is again an orientable surface with
![]() $\partial S = q^{-1}(\partial T) = q^{-1}(\alpha ) = \alpha _1 \cup \ldots \cup \alpha _m$
. The surface
$\partial S = q^{-1}(\partial T) = q^{-1}(\alpha ) = \alpha _1 \cup \ldots \cup \alpha _m$
. The surface
![]() $S$
is homotopy-equivalent to
$S$
is homotopy-equivalent to
![]() $Y$
. For
$Y$
. For
![]() $i=1,\ldots,m$
let
$i=1,\ldots,m$
let
![]() $[\alpha _i] \in H_1(S;\;{\mathbb{C}})$
be the homology class represented by
$[\alpha _i] \in H_1(S;\;{\mathbb{C}})$
be the homology class represented by
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $[\partial S] \;:\!=\; \sum _{i=1}^m[\alpha _i] \in H_1(S;\;{\mathbb{C}})$
the homology class represented by
$[\partial S] \;:\!=\; \sum _{i=1}^m[\alpha _i] \in H_1(S;\;{\mathbb{C}})$
the homology class represented by
![]() $\partial S$
. Denote by
$\partial S$
. Denote by
![]() ${\mathbb{C}}[\alpha _i]$
and
${\mathbb{C}}[\alpha _i]$
and
![]() ${\mathbb{C}}[\partial S]$
their respective
${\mathbb{C}}[\partial S]$
their respective
![]() $\mathbb{C}$
-spans. Let
$\mathbb{C}$
-spans. Let
![]() $\bigoplus _{i=1}^m{\mathbb{C}} [ \alpha _i ]$
be the
$\bigoplus _{i=1}^m{\mathbb{C}} [ \alpha _i ]$
be the
![]() $m$
-dimensional
$m$
-dimensional
![]() $G$
-representation, where
$G$
-representation, where
![]() $G$
acts by permuting the homology classes
$G$
acts by permuting the homology classes
![]() $[\alpha _i]$
. We then have the following short exact sequence of
$[\alpha _i]$
. We then have the following short exact sequence of
![]() $G$
-representations:
$G$
-representations:
where the map
![]() $\psi$
is given by
$\psi$
is given by
![]() $z \mapsto (z,\ldots,z)$
, and
$z \mapsto (z,\ldots,z)$
, and
![]() $\varphi$
sends
$\varphi$
sends
![]() $(z_1, \ldots, z_m)$
to
$(z_1, \ldots, z_m)$
to
![]() $\sum _{i=1}^m z_i [\alpha _i]$
. One can verify that
$\sum _{i=1}^m z_i [\alpha _i]$
. One can verify that
![]() $\psi$
and
$\psi$
and
![]() $\varphi$
are
$\varphi$
are
![]() $G$
-equivariant. The exactness follows, for example, from the exactness of the long exact sequence of the pair
$G$
-equivariant. The exactness follows, for example, from the exactness of the long exact sequence of the pair
![]() $(S,\partial S)$
.
$(S,\partial S)$
.
Recall that we are interested in understanding
![]() $\textrm{Span}_{H_1(S;{\mathbb{C}})} \{ [\alpha _1], \ldots, [\alpha _m] \}$
. Using the short exact sequence, it is enough to understand
$\textrm{Span}_{H_1(S;{\mathbb{C}})} \{ [\alpha _1], \ldots, [\alpha _m] \}$
. Using the short exact sequence, it is enough to understand
![]() $\bigoplus _{i=1}^m{\mathbb{C}} [ \alpha _i ]$
and
$\bigoplus _{i=1}^m{\mathbb{C}} [ \alpha _i ]$
and
![]() ${\mathbb{C}} [\partial S]$
as
${\mathbb{C}} [\partial S]$
as
![]() $G$
-representations. Let us assume without loss of generality that
$G$
-representations. Let us assume without loss of generality that
![]() $\alpha _1$
contains the base point
$\alpha _1$
contains the base point
![]() $s_0 \in S$
. Then,
$s_0 \in S$
. Then,
since
![]() $\alpha$
is simple. The curves
$\alpha$
is simple. The curves
![]() $\alpha _1, \ldots, \alpha _m$
are the elevations of
$\alpha _1, \ldots, \alpha _m$
are the elevations of
![]() $\alpha$
, and
$\alpha$
, and
![]() $G$
permutes these. Hence, we can identify the curves
$G$
permutes these. Hence, we can identify the curves
![]() $\alpha _2, \ldots, \alpha _m$
with the left cosets of
$\alpha _2, \ldots, \alpha _m$
with the left cosets of
![]() $K$
in
$K$
in
![]() $G$
, because
$G$
, because
![]() $K$
is the stabilizer of
$K$
is the stabilizer of
![]() $\alpha _1$
. Choose representatives
$\alpha _1$
. Choose representatives
![]() $g_1 = 1_G, g_2, \ldots, g_m \in G$
of the left cosets of
$g_1 = 1_G, g_2, \ldots, g_m \in G$
of the left cosets of
![]() $K$
in
$K$
in
![]() $G$
. Then,
$G$
. Then,
as
![]() $G$
-representations by the defining property of the induced representation. Clearly,
$G$
-representations by the defining property of the induced representation. Clearly,
![]() $G$
acts trivially on
$G$
acts trivially on
![]() $[\partial S]$
. Thus, we have proved the proposition, since by the exactness of the short exact sequence above we have
$[\partial S]$
. Thus, we have proved the proposition, since by the exactness of the short exact sequence above we have
It turns out that the above representation-theoretic property is in general not sufficient to characterize homology classes of elevations of primitive commutators. A counterexample for
![]() $n=2$
will be given in Proposition 1.3, whose construction is based on the idea of stacking covers and the proof of Theorem 1.1. We need some preliminary considerations.
$n=2$
will be given in Proposition 1.3, whose construction is based on the idea of stacking covers and the proof of Theorem 1.1. We need some preliminary considerations.
For a group
![]() $G$
, a subgroup
$G$
, a subgroup
![]() $H \leq G$
is characteristic if it is invariant under every automorphism of
$H \leq G$
is characteristic if it is invariant under every automorphism of
![]() $G$
, that is, for all
$G$
, that is, for all
![]() $\varphi \in \textrm{Aut}(G)$
we have
$\varphi \in \textrm{Aut}(G)$
we have
![]() $\varphi (H) \subseteq H$
. If we have a sequence of subgroups of the form
$\varphi (H) \subseteq H$
. If we have a sequence of subgroups of the form
![]() $K \mathrel{\unlhd }_{\textrm{char}} H \mathrel{\unlhd } G$
with
$K \mathrel{\unlhd }_{\textrm{char}} H \mathrel{\unlhd } G$
with
![]() $K$
characteristic in
$K$
characteristic in
![]() $H$
and
$H$
and
![]() $H$
normal in
$H$
normal in
![]() $G$
, then
$G$
, then
![]() $K$
is also normal in
$K$
is also normal in
![]() $G$
.
$G$
.
Example 3.1.
For all
![]() $n,m \geq 2$
the
$n,m \geq 2$
the
![]() $\textrm{mod} \, \textrm{m}$
-homology cover is a characteristic cover of the wedge of
$\textrm{mod} \, \textrm{m}$
-homology cover is a characteristic cover of the wedge of
![]() $\textrm{n}$
circles. Recall that the
$\textrm{n}$
circles. Recall that the
![]() $\textrm{mod} \, \textrm{m}$
-homology cover is given by the surjective group homomorphism:
$\textrm{mod} \, \textrm{m}$
-homology cover is given by the surjective group homomorphism:
It suffices to verify that
![]() $\ker\!(\phi )$
is characteristic in
$\ker\!(\phi )$
is characteristic in
![]() $F_n$
. Let
$F_n$
. Let
![]() $\alpha \in \textrm{Aut}(F_n)$
. Since
$\alpha \in \textrm{Aut}(F_n)$
. Since
![]() $\ker\!(\phi ) = \langle [x,y], z^m \mid x, y, z \in F_n \rangle$
, we conclude that
$\ker\!(\phi ) = \langle [x,y], z^m \mid x, y, z \in F_n \rangle$
, we conclude that
![]() $\alpha (\!\ker\!(\phi )) \subseteq \ker\!(\phi )$
, and hence that the cover is characteristic.
$\alpha (\!\ker\!(\phi )) \subseteq \ker\!(\phi )$
, and hence that the cover is characteristic.
The
![]() $\textrm{mod} \, 2$
-homology cover has the additional property that all primitive commutators lift to primitive elements.
$\textrm{mod} \, 2$
-homology cover has the additional property that all primitive commutators lift to primitive elements.
Lemma 3.2.
Let
![]() $\phi \;:\; F_2 \to (\mathbb{Z}/ 2 \mathbb{Z})^2$
be the
$\phi \;:\; F_2 \to (\mathbb{Z}/ 2 \mathbb{Z})^2$
be the
![]() $\textrm{mod} \, 2$
-homology cover as in Example 3.1. Then for
$\textrm{mod} \, 2$
-homology cover as in Example 3.1. Then for
![]() $x \;:\!=\; [l,l']$
any primitive commutator in
$x \;:\!=\; [l,l']$
any primitive commutator in
![]() $F_2$
with
$F_2$
with
![]() $l \neq l'$
, its preferred elevation is primitive.
$l \neq l'$
, its preferred elevation is primitive.
Proof. We denote by
![]() $p \;:\; (Y, y_0) \to (X,x_0)$
the associated finite, characteristic cover, where
$p \;:\; (Y, y_0) \to (X,x_0)$
the associated finite, characteristic cover, where
![]() $(X,x_0)$
is the wedge of two circles and
$(X,x_0)$
is the wedge of two circles and
![]() $x_0$
the point of identification. Let
$x_0$
the point of identification. Let
![]() $x_1$
and
$x_1$
and
![]() $x_2$
be generators of the fundamental groups of the two circles. We will show the claim for
$x_2$
be generators of the fundamental groups of the two circles. We will show the claim for
![]() $x \;:\!=\; [x_1, x_2]$
first. Then,
$x \;:\!=\; [x_1, x_2]$
first. Then,
![]() $\phi (x)=0$
and thus
$\phi (x)=0$
and thus
![]() $x$
lifts to a closed curve on
$x$
lifts to a closed curve on
![]() $Y$
illustrated by the dotted lines.
$Y$
illustrated by the dotted lines.

We need to extend
![]() $x$
to a free basis of
$x$
to a free basis of
![]() $\pi _1(Y, y_0)$
. For example,
$\pi _1(Y, y_0)$
. For example,
is a free basis of
![]() $\pi _1(Y, y_0)$
. Namely, consider the spanning tree illustrated by the bold lines in the above figure.
$\pi _1(Y, y_0)$
. Namely, consider the spanning tree illustrated by the bold lines in the above figure.
For
![]() $x'$
any primitive commutator, we use that there exists a homotopy equivalence of
$x'$
any primitive commutator, we use that there exists a homotopy equivalence of
![]() $X$
that sends
$X$
that sends
![]() $x'$
to
$x'$
to
![]() $x$
, since the primitive elements defining
$x$
, since the primitive elements defining
![]() $x'$
form a basis of
$x'$
form a basis of
![]() $F_2$
. Since the cover is characteristic, this homotopy equivalence can be lifted to
$F_2$
. Since the cover is characteristic, this homotopy equivalence can be lifted to
![]() $Y$
, and the same argument works.
$Y$
, and the same argument works.
There is one last remark before we prove Proposition 1.3. If
![]() $p \;:\; Z \to X$
and
$p \;:\; Z \to X$
and
![]() $q \;:\; Y \to Z$
are finite, regular covers with base points
$q \;:\; Y \to Z$
are finite, regular covers with base points
![]() $z_0 \in p^{-1}(x_0)$
and
$z_0 \in p^{-1}(x_0)$
and
![]() $y_0 \in q^{-1}(z_0)$
, respectively, such that
$y_0 \in q^{-1}(z_0)$
, respectively, such that
![]() $p \circ q \;:\; Y \to X$
is a finite, regular cover, then for
$p \circ q \;:\; Y \to X$
is a finite, regular cover, then for
![]() $l$
any loop on
$l$
any loop on
![]() $X$
, we have by the uniqueness of lifts and the choice of base points that
$X$
, we have by the uniqueness of lifts and the choice of base points that
Proof of Proposition 1.3. Recall that for
![]() $n=2$
, we would like to prove the existence of a finite, regular cover
$n=2$
, we would like to prove the existence of a finite, regular cover
![]() $p \;:\; Y \to X$
, together with
$p \;:\; Y \to X$
, together with
![]() $z \in H_1(Y;\;\mathbb{Z}) \cap \ker\!(p_*)$
indivisible such that
$z \in H_1(Y;\;\mathbb{Z}) \cap \ker\!(p_*)$
indivisible such that
-
(i)
 $\textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}_{\langle g \rangle }^G({\mathbb{C}}_{\textrm{triv}})/{\mathbb{C}}_{\textrm{triv}}$
for some
$\textrm{Span}_{{\mathbb{C}} [G]} \{z\} \cong \textrm{Ind}_{\langle g \rangle }^G({\mathbb{C}}_{\textrm{triv}})/{\mathbb{C}}_{\textrm{triv}}$
for some
 $g \in G$
, where
$g \in G$
, where
 $G$
is the deck group associated with the cover
$G$
is the deck group associated with the cover
 $p$
, and
$p$
, and -
(ii)
 $z$
cannot be represented by an elevation of a primitive commutator in
$z$
cannot be represented by an elevation of a primitive commutator in
 $X$
.
$X$
.
We will construct
![]() $Y$
using iterated covers. Let
$Y$
using iterated covers. Let
![]() $\pi _1(X) \cong F_2$
be the free group on the generators
$\pi _1(X) \cong F_2$
be the free group on the generators
![]() $x_1$
and
$x_1$
and
![]() $x_2$
. Consider the primitive commutators
$x_2$
. Consider the primitive commutators
![]() $ x' \;:\!=\; [x_1,x_2], \; x'' \;:\!=\; [x_2^{-1},x_1]$
. We start with the
$ x' \;:\!=\; [x_1,x_2], \; x'' \;:\!=\; [x_2^{-1},x_1]$
. We start with the
![]() $\textrm{mod} \, 2$
-homology cover
$\textrm{mod} \, 2$
-homology cover
![]() $p_1 \;:\; Z \to X$
defined by the surjective homomorphism:
$p_1 \;:\; Z \to X$
defined by the surjective homomorphism:
Then
![]() $l' \;:\!=\; \tilde{x}'$
and
$l' \;:\!=\; \tilde{x}'$
and
![]() $l'' \;:\!=\; \tilde{x}''$
are primitive in
$l'' \;:\!=\; \tilde{x}''$
are primitive in
![]() $\pi _1(Z)$
by Lemma 3.2. We additionally have that
$\pi _1(Z)$
by Lemma 3.2. We additionally have that
![]() $l'$
and
$l'$
and
![]() $l''$
lie in one basis. For example, the elements
$l''$
lie in one basis. For example, the elements
![]() $x_1^2$
,
$x_1^2$
,
![]() $x_2^2$
and
$x_2^2$
and
![]() $x_2 x_1^2 x_2^{-1}$
complete
$x_2 x_1^2 x_2^{-1}$
complete
![]() $l'$
and
$l'$
and
![]() $l''$
to a basis of
$l''$
to a basis of
![]() $\pi _1(Z)\cong F_5$
, using the same notation as in the proof of Lemma 3.2.
$\pi _1(Z)\cong F_5$
, using the same notation as in the proof of Lemma 3.2.
Consider now the
![]() $\textrm{mod} \, 2$
-homology cover
$\textrm{mod} \, 2$
-homology cover
![]() $p_2 \;:\; Y \to Z$
defined by the surjection:
$p_2 \;:\; Y \to Z$
defined by the surjection:
and extension. Then
![]() $p \;:\!=\; p_1 \circ p_2 \;:\; Y \to X$
is a finite, regular cover because
$p \;:\!=\; p_1 \circ p_2 \;:\; Y \to X$
is a finite, regular cover because
![]() $p_2$
is characteristic, and we denote its deck group by
$p_2$
is characteristic, and we denote its deck group by
![]() $G$
. We have the following short exact sequence of groups
$G$
. We have the following short exact sequence of groups
![]() $ 1 \to N \to G \to Q \to 1$
. Since
$ 1 \to N \to G \to Q \to 1$
. Since
![]() $0=[x']=[x''] \in H_1(X;\;\mathbb{Z})$
, it follows that
$0=[x']=[x''] \in H_1(X;\;\mathbb{Z})$
, it follows that
We write
![]() $z' = z'_{\!\!1}+\ldots +z'_{\!\!2^5}$
and
$z' = z'_{\!\!1}+\ldots +z'_{\!\!2^5}$
and
![]() $z''= z''_{\!\!\!1}+\ldots +z''_{\!\!\!2^5}$
with
$z''= z''_{\!\!\!1}+\ldots +z''_{\!\!\!2^5}$
with
![]() $ z'_{\!\!i}, z''_{\!\!\!i} \in M(W_i)$
, where
$ z'_{\!\!i}, z''_{\!\!\!i} \in M(W_i)$
, where
![]() $W_1 ={\mathbb{C}}_{\textrm{triv}}, W_2, \ldots, W_{2^5}$
are representatives of the isomorphism classes of the irreducible representations of
$W_1 ={\mathbb{C}}_{\textrm{triv}}, W_2, \ldots, W_{2^5}$
are representatives of the isomorphism classes of the irreducible representations of
![]() $N$
. Define
$N$
. Define
![]() $\hat{z} \;:\!=\; z'-(z'_{\!\!1}-z''_{\!\!\!1})$
. Then,
$\hat{z} \;:\!=\; z'-(z'_{\!\!1}-z''_{\!\!\!1})$
. Then,
![]() $\hat{z}$
still lies in the kernel of
$\hat{z}$
still lies in the kernel of
![]() $p_*$
: Indeed, since
$p_*$
: Indeed, since
![]() $(p_2)_*(z')=(p_2)_*(z''_{\!\!\!1})$
we have
$(p_2)_*(z')=(p_2)_*(z''_{\!\!\!1})$
we have
and consequently,
![]() $p_*(\hat{z})= (p_1)_* ((p_2)_*(\hat{z}))= (p_1)_* ((p_2)_*(z''))=p_*(z'') = 0$
, since
$p_*(\hat{z})= (p_1)_* ((p_2)_*(\hat{z}))= (p_1)_* ((p_2)_*(z''))=p_*(z'') = 0$
, since
![]() $z'' \in \ker\!(p_*)$
.
$z'' \in \ker\!(p_*)$
.
By the same argument as in the proof of Theorem 1.1,
![]() $\hat{z} \in H_1(Y;\;\mathbb{Q})$
and we can choose
$\hat{z} \in H_1(Y;\;\mathbb{Q})$
and we can choose
![]() $q\in \mathbb{Q}$
such that
$q\in \mathbb{Q}$
such that
![]() $z \;:\!=\; q \hat{z} \in \ker\!(p_*) \leq H_1(Y;\;\mathbb{Z})$
is indivisible. Using that
$z \;:\!=\; q \hat{z} \in \ker\!(p_*) \leq H_1(Y;\;\mathbb{Z})$
is indivisible. Using that
![]() $N$
is Abelian, we can now copy the same idea as in the proof of Theorem 1.1 to obtain that
$N$
is Abelian, we can now copy the same idea as in the proof of Theorem 1.1 to obtain that
![]() $z$
is not the homology class of an elevation of a primitive element in
$z$
is not the homology class of an elevation of a primitive element in
![]() $Z$
and thus also not the homology class of an elevation of a primitive commutator in
$Z$
and thus also not the homology class of an elevation of a primitive commutator in
![]() $X$
by Lemma 3.2.
$X$
by Lemma 3.2.
4. Primitive commutator homology
The first step in attacking the question whether
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) = \ker\!(p_*)$
is the obstruction in Theorem 1.4. We adapt the ideas of the proof of [Reference Farb and Hensel3, Theorem 1.4].
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) = \ker\!(p_*)$
is the obstruction in Theorem 1.4. We adapt the ideas of the proof of [Reference Farb and Hensel3, Theorem 1.4].
Proof of Theorem 1.4. We would like to prove that if
![]() $V$
is an irreducible
$V$
is an irreducible
![]() $G$
-representation that appears in
$G$
-representation that appears in
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})$
, then
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})$
, then
![]() $V \in \textrm{Irr}^{\textrm{comm}}(\phi,G) \setminus \{{\mathbb{C}}_{\textrm{triv}}\}$
. Since
$V \in \textrm{Irr}^{\textrm{comm}}(\phi,G) \setminus \{{\mathbb{C}}_{\textrm{triv}}\}$
. Since
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \leq \ker\!(p_*) \cong \bigoplus _{i=2}^{k(G)} M(V_i)$
by Lemma 2.3(b), it is clear that
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \leq \ker\!(p_*) \cong \bigoplus _{i=2}^{k(G)} M(V_i)$
by Lemma 2.3(b), it is clear that
![]() $V\neq{\mathbb{C}}_{\textrm{triv}}$
.
$V\neq{\mathbb{C}}_{\textrm{triv}}$
.
Let
![]() $x=[l,l']$
be a primitive commutator in
$x=[l,l']$
be a primitive commutator in
![]() $F_n$
, and set
$F_n$
, and set
![]() $K \;:\!=\; \langle \phi (x) \rangle \leq \langle \phi (l), \phi (l') \rangle \;=\!:\; H \leq G$
. Let
$K \;:\!=\; \langle \phi (x) \rangle \leq \langle \phi (l), \phi (l') \rangle \;=\!:\; H \leq G$
. Let
![]() $V$
be an irreducible
$V$
be an irreducible
![]() $G$
-representation. Then writing
$G$
-representation. Then writing
![]() $V^{K} = \{v \in V \;:\; gv=v \textrm{ for all } g \in K \}$
for the space of fixed points of
$V^{K} = \{v \in V \;:\; gv=v \textrm{ for all } g \in K \}$
for the space of fixed points of
![]() $K$
, Proposition 1.2 and Frobenius reciprocity (see e.g. [Reference Isaacs6, Lemma 5.2]) imply that
$K$
, Proposition 1.2 and Frobenius reciprocity (see e.g. [Reference Isaacs6, Lemma 5.2]) imply that
where the last equality follows from the orthogonality relations.
An irreducible representation
![]() $V$
appears in
$V$
appears in
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})$
if and only if there exists a primitive commutator
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})$
if and only if there exists a primitive commutator
![]() $x=[l,l']$
in
$x=[l,l']$
in
![]() $F_n$
such that
$F_n$
such that
By the above, this implies
![]() $\dim\!(V^{K}) \neq 0$
, which is equivalent to the existence of some nonzero
$\dim\!(V^{K}) \neq 0$
, which is equivalent to the existence of some nonzero
![]() $v \in V$
with
$v \in V$
with
![]() $\phi (x)(v) = v$
. Thus, for
$\phi (x)(v) = v$
. Thus, for
![]() $V$
to appear in
$V$
to appear in
![]() $\textrm{Span}_{{\mathbb{C}} [G]} \{ [\tilde{x}] \}$
, we necessarily need
$\textrm{Span}_{{\mathbb{C}} [G]} \{ [\tilde{x}] \}$
, we necessarily need
![]() $V \in \textrm{Irr}^{\textrm{comm}}(\phi,G)$
.
$V \in \textrm{Irr}^{\textrm{comm}}(\phi,G)$
.
We will continue by studying
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})$
in some examples. If
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})$
in some examples. If
![]() $n=2$
and
$n=2$
and
![]() $G$
is Abelian, we have
$G$
is Abelian, we have
![]() $\phi (x_{12})=1_G$
and we obtain by the semisimplicity of
$\phi (x_{12})=1_G$
and we obtain by the semisimplicity of
![]() $M=H_1(Y;\;{\mathbb{C}})$
that
$M=H_1(Y;\;{\mathbb{C}})$
that
This implies that
![]() $\textrm{Span}_{{\mathbb{C}} [G]} \{ [\tilde{x}_{12}] \} \cong \ker\!(p_*)$
by Lemma 2.3(b), and therefore
$\textrm{Span}_{{\mathbb{C}} [G]} \{ [\tilde{x}_{12}] \} \cong \ker\!(p_*)$
by Lemma 2.3(b), and therefore
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})=\ker\!(p_*)$
.
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})=\ker\!(p_*)$
.
On the other hand, there are examples in rank 2 with
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})\neq \ker\!(p_*)$
, since not every irreducible representation has the property that the image of a primitive commutator has a nonzero fixed point, in other words
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}})\neq \ker\!(p_*)$
, since not every irreducible representation has the property that the image of a primitive commutator has a nonzero fixed point, in other words
![]() $\textrm{Irr}^{\textrm{comm}}(\phi, G) \neq \textrm{Irr}(G)$
.
$\textrm{Irr}^{\textrm{comm}}(\phi, G) \neq \textrm{Irr}(G)$
.
Example 4.1.
For
![]() $n=2$
any surjective homomorphism
$n=2$
any surjective homomorphism
![]() $\phi \;:\; F_2 \to S_3$
, where
$\phi \;:\; F_2 \to S_3$
, where
![]() $S_3$
denotes the symmetric group on three elements, satisfies
$S_3$
denotes the symmetric group on three elements, satisfies
![]() $\textrm{Irr}^{\textrm{comm}}(\phi, S_3) \neq \textrm{Irr}(S_3)$
. In fact, the irreducible two-dimensional representation of
$\textrm{Irr}^{\textrm{comm}}(\phi, S_3) \neq \textrm{Irr}(S_3)$
. In fact, the irreducible two-dimensional representation of
![]() $S_3$
does not lie in
$S_3$
does not lie in
![]() $\textrm{Irr}^{\textrm{comm}}(\phi, S_3)$
. It can be realized by
$\textrm{Irr}^{\textrm{comm}}(\phi, S_3)$
. It can be realized by
![]() $S_3$
acting on
$S_3$
acting on
![]() $V\;:\!=\;{\mathbb{C}}^3/\langle e_1+e_2+e_3\rangle$
by permutation of the coordinates. Since
$V\;:\!=\;{\mathbb{C}}^3/\langle e_1+e_2+e_3\rangle$
by permutation of the coordinates. Since
![]() $\phi$
is surjective, the image of a primitive commutator is either the cycle
$\phi$
is surjective, the image of a primitive commutator is either the cycle
![]() $(1 2 3)$
or
$(1 2 3)$
or
![]() $(1 3 2)$
. Computing the action of
$(1 3 2)$
. Computing the action of
![]() $(123)$
on
$(123)$
on
![]() $V$
, we see that one is not an eigenvalue, so
$V$
, we see that one is not an eigenvalue, so
![]() $(123)$
does not have a fixed vector. Similarly for
$(123)$
does not have a fixed vector. Similarly for
![]() $(132)$
. Thus,
$(132)$
. Thus,
![]() $V \notin \textrm{Irr}^{\textrm{comm}}(\phi, S_3)$
.
$V \notin \textrm{Irr}^{\textrm{comm}}(\phi, S_3)$
.
A more general answer to this question is presented in the following for every
![]() $n \geq 2$
. To see that there are examples where
$n \geq 2$
. To see that there are examples where
![]() $H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \neq \ker\!(p_*)$
for certain covers
$H_1^{\textrm{comm}}(Y;\;{\mathbb{C}}) \neq \ker\!(p_*)$
for certain covers
![]() $p \;:\; Y \to X$
, we use iterated covers to relate the question to the one for primitive homology. Note that in general the composition of two regular covers is not again regular, but every finite, regular cover is itself covered by a finite, characteristic cover. This is true by the following observation: if
$p \;:\; Y \to X$
, we use iterated covers to relate the question to the one for primitive homology. Note that in general the composition of two regular covers is not again regular, but every finite, regular cover is itself covered by a finite, characteristic cover. This is true by the following observation: if
![]() $G$
is a finitely generated group and
$G$
is a finitely generated group and
![]() $H \mathrel{\unlhd } G$
a normal subgroup of finite index
$H \mathrel{\unlhd } G$
a normal subgroup of finite index
![]() $k$
, then there is a subgroup
$k$
, then there is a subgroup
![]() $H^* \leq H$
which is of finite index in
$H^* \leq H$
which is of finite index in
![]() $G$
and characteristic in
$G$
and characteristic in
![]() $G$
. Namely, we can take
$G$
. Namely, we can take
![]() $H^* \;:\!=\; \bigcap _{H^{\prime} \mathrel{\unlhd } G \textrm{ normal}, \,[G:H^{\prime}]=k} H'$
.
$H^* \;:\!=\; \bigcap _{H^{\prime} \mathrel{\unlhd } G \textrm{ normal}, \,[G:H^{\prime}]=k} H'$
.
In order to prove that in general
![]() $H_1^{\textrm{comm}} \neq \ker\!(p_*)$
, we reduce the case of primitive commutator homology to the case of primitive homology by looking at the
$H_1^{\textrm{comm}} \neq \ker\!(p_*)$
, we reduce the case of primitive commutator homology to the case of primitive homology by looking at the
![]() $\textrm{mod} \, 2$
-homology cover. The proof of Lemma 3.2 can be generalized to show that for every
$\textrm{mod} \, 2$
-homology cover. The proof of Lemma 3.2 can be generalized to show that for every
![]() $n$
, the
$n$
, the
![]() $\textrm{mod} \, 2$
-homology cover as in Example 3.1 has the property that primitive commutators lift to primitive elements. Then, we can apply the result of Malestein and Putman in [Reference Malestein and Putman9, Example 1.3] to conclude. For this, we need to understand how primitive homology behaves in iterated covers. To avoid confusion, we introduce the following notation: if
$\textrm{mod} \, 2$
-homology cover as in Example 3.1 has the property that primitive commutators lift to primitive elements. Then, we can apply the result of Malestein and Putman in [Reference Malestein and Putman9, Example 1.3] to conclude. For this, we need to understand how primitive homology behaves in iterated covers. To avoid confusion, we introduce the following notation: if
![]() $Y \to X$
is a finite, regular cover of finite graphs, we will from now on write
$Y \to X$
is a finite, regular cover of finite graphs, we will from now on write
![]() $H_1^S(Y \to X;\;{\mathbb{C}})$
instead of
$H_1^S(Y \to X;\;{\mathbb{C}})$
instead of
![]() $H_1^S(Y;\;{\mathbb{C}})$
.
$H_1^S(Y;\;{\mathbb{C}})$
.
Lemma 4.2.
Let
![]() $q \;:\; Z \to Y$
and
$q \;:\; Z \to Y$
and
![]() $p \;:\; Y \to X$
be finite, regular covers of finite graphs such that
$p \;:\; Y \to X$
be finite, regular covers of finite graphs such that
![]() $p \circ q \;:\; Z \to X$
is a finite, regular cover. Then
$p \circ q \;:\; Z \to X$
is a finite, regular cover. Then
In other words, primitive homology gets mapped into primitive homology.
Proof. For
![]() $l$
a primitive element in
$l$
a primitive element in
![]() $\pi _1(X)$
, we have for some
$\pi _1(X)$
, we have for some
![]() $k \in \mathbb{Z}$
$k \in \mathbb{Z}$
Corollary 4.3.
Let the setup be as in Lemma 4.2 with the condition that
![]() $H_1^{\textrm{prim}}(Y \to X;\;{\mathbb{C}}) \neq H_1(Y;\;{\mathbb{C}})$
as
$H_1^{\textrm{prim}}(Y \to X;\;{\mathbb{C}}) \neq H_1(Y;\;{\mathbb{C}})$
as
![]() $K$
-representations where
$K$
-representations where
![]() $K \;:\!=\; \textrm{Deck}(Y,p)$
. Then,
$K \;:\!=\; \textrm{Deck}(Y,p)$
. Then,
as
![]() $G$
-representations with
$G$
-representations with
![]() $G \;:\!=\; \textrm{Deck}(Z,p \circ q)$
.
$G \;:\!=\; \textrm{Deck}(Z,p \circ q)$
.
Proof. This is straightforward using that
![]() $q_* \;:\; H_1(Z;\;{\mathbb{C}}) \to H_1(Y;\;{\mathbb{C}})$
is surjective.
$q_* \;:\; H_1(Z;\;{\mathbb{C}}) \to H_1(Y;\;{\mathbb{C}})$
is surjective.
The last corollary implies that we can assume without loss of generality that the cover constructed by Malestein and Putman in [Reference Malestein and Putman9, Example 1.3] is characteristic by passing to a finite, characteristic cover, which will satisfy that primitive homology is not all of homology. We bring everything together in the following proof.
Proof of Theorem 1.5. Recall that for every
![]() $n \geq 2$
we would like to construct a finite, regular cover
$n \geq 2$
we would like to construct a finite, regular cover
![]() $p \;:\; Z \to X$
such that
$p \;:\; Z \to X$
such that
![]() $H_1^{\textrm{comm}}(Z \to X;\;{\mathbb{C}}) \neq \ker\!(p_*)$
.
$H_1^{\textrm{comm}}(Z \to X;\;{\mathbb{C}}) \neq \ker\!(p_*)$
.
Let
![]() $p' \;:\; Y \to X$
be the
$p' \;:\; Y \to X$
be the
![]() $\textrm{mod} \, 2$
-homology cover with group of deck transformations
$\textrm{mod} \, 2$
-homology cover with group of deck transformations
![]() $K= (\mathbb{Z}/ 2 \mathbb{Z})^n$
. By Example 3.1, we know that this cover is characteristic. Lemma 3.2 tells us that all primitive commutators in
$K= (\mathbb{Z}/ 2 \mathbb{Z})^n$
. By Example 3.1, we know that this cover is characteristic. Lemma 3.2 tells us that all primitive commutators in
![]() $X$
lift to primitive elements in
$X$
lift to primitive elements in
![]() $Y$
. The space
$Y$
. The space
![]() $Y$
is again a connected graph with free fundamental group, so we can apply the result of Malestein and Putman, see [Reference Malestein and Putman9, Theorem C, Example 1.3], to find a finite, regular cover
$Y$
is again a connected graph with free fundamental group, so we can apply the result of Malestein and Putman, see [Reference Malestein and Putman9, Theorem C, Example 1.3], to find a finite, regular cover
![]() $q \;:\; Z \to Y$
with deck group
$q \;:\; Z \to Y$
with deck group
![]() $H$
such that
$H$
such that
as
![]() $H$
-representations. By the above considerations, we can assume that this cover is characteristic. Therefore,
$H$
-representations. By the above considerations, we can assume that this cover is characteristic. Therefore,
![]() $p \;:\!=\; p' \circ q \;:\; Z \to X$
is regular. Denote its deck group by
$p \;:\!=\; p' \circ q \;:\; Z \to X$
is regular. Denote its deck group by
![]() $G$
.
$G$
.

Let us assume for a contradiction that
![]() $H_1^{\textrm{comm}}(Z \to X;\;{\mathbb{C}}) = \ker\!(p_*)$
. Then Lemma 2.3(b) implies that
$H_1^{\textrm{comm}}(Z \to X;\;{\mathbb{C}}) = \ker\!(p_*)$
. Then Lemma 2.3(b) implies that
![]() $H_1^{\textrm{comm}}(Z \to X;\;{\mathbb{C}}) = \bigoplus _{i=2}^{k(G)} M(V_i),$
with
$H_1^{\textrm{comm}}(Z \to X;\;{\mathbb{C}}) = \bigoplus _{i=2}^{k(G)} M(V_i),$
with
![]() $M=H_1(Z;\;{\mathbb{C}})$
as
$M=H_1(Z;\;{\mathbb{C}})$
as
![]() $G$
-representations. We also know by Lemma 2.3(a) that
$G$
-representations. We also know by Lemma 2.3(a) that
By definition, we have
![]() $p_\#([l]) = \sum _{g \in G} g \, [\tilde{l}]$
. For
$p_\#([l]) = \sum _{g \in G} g \, [\tilde{l}]$
. For
![]() $l$
a primitive element, it follows that
$l$
a primitive element, it follows that
![]() $p_\#([l]) \in H_1^{\textrm{prim}}(Z;\;{\mathbb{C}})$
. Thus, we obtain
$p_\#([l]) \in H_1^{\textrm{prim}}(Z;\;{\mathbb{C}})$
. Thus, we obtain
![]() $M(V_1) \leq H_1^{\textrm{prim}}(Z \to X;\;{\mathbb{C}})$
. This implies that
$M(V_1) \leq H_1^{\textrm{prim}}(Z \to X;\;{\mathbb{C}})$
. This implies that
We would like to conclude from this equality that
![]() $H_1(Z;\;{\mathbb{C}}) \leq H_1^{\textrm{prim}}(Z \to Y;\;{\mathbb{C}})$
, which contradicts the choice of the cover
$H_1(Z;\;{\mathbb{C}}) \leq H_1^{\textrm{prim}}(Z \to Y;\;{\mathbb{C}})$
, which contradicts the choice of the cover
![]() $q \;:\; Z \to Y$
. We know that lifts of primitive elements are primitive, and by Lemma 3.2 that for the
$q \;:\; Z \to Y$
. We know that lifts of primitive elements are primitive, and by Lemma 3.2 that for the
![]() $\textrm{mod} \, 2$
-homology cover primitive commutators in
$\textrm{mod} \, 2$
-homology cover primitive commutators in
![]() $X$
also lift to primitive elements in
$X$
also lift to primitive elements in
![]() $Y$
. Set
$Y$
. Set
Then
![]() $S \subseteq \{l \in \pi _1(Y) \textrm{ primitive} \}$
. Clearly, for any two subsets
$S \subseteq \{l \in \pi _1(Y) \textrm{ primitive} \}$
. Clearly, for any two subsets
![]() $S' \subseteq S'' \subseteq F_m$
we have
$S' \subseteq S'' \subseteq F_m$
we have
![]() $H_1^{S^{\prime}}(Y;\;{\mathbb{C}}) \leq H_1^{S^{\prime\prime}}(Y;\;{\mathbb{C}})$
. By the above equation together with the last observation, we obtain
$H_1^{S^{\prime}}(Y;\;{\mathbb{C}}) \leq H_1^{S^{\prime\prime}}(Y;\;{\mathbb{C}})$
. By the above equation together with the last observation, we obtain
Competing interests
The author declares none.
Acknowledgments
I would like to thank Sebastian Hensel for introducing me to this topic and for his helpful remarks. Thanks goes as well to Bram Petri for valuable input, and Peter Feller, Gerhard Hiss and Anna Ribelles Pérez for constructive discussions and feedback. I am grateful to the referee for the detailed comments and suggestions, particularly for pointing out an error in the original argument for Corollary 2.5.