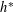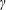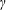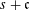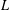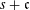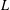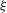We investigate arithmetic, geometric and combinatorial properties of symmetric edge polytopes. We give a complete combinatorial description of their facets. By combining Gröbner basis techniques, half-open decompositions and methods for interlacing polynomials we provide an explicit formula for the $h^{\ast }$-polynomial in case of complete bipartite graphs. In particular, we show that the $h^{\ast }$-polynomial is $\unicode[STIX]{x1D6FE}$-positive and real-rooted. This proves Gal’s conjecture for arbitrary flag unimodular triangulations in this case, and, beyond that, we prove a strengthening due to Nevo and Petersen [On $\unicode[STIX]{x1D6FE}$-vectors satisfying the Kruskal–Katona inequalities. Discrete Comput. Geom.45(3) (2011), 503–521].

We continue our study of intermediate sums over polyhedra, interpolating between integrals and discrete sums, which were introduced by Barvinok [Computing the Ehrhart quasi-polynomial of a rational simplex. Math. Comp. 75 (2006), 1449–1466]. By well-known decompositions, it is sufficient to consider the case of affine cones 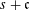$s+\mathfrak{c}$ , where $s$ is an arbitrary real vertex and $\mathfrak{c}$ is a rational polyhedral cone. For a given rational subspace 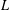 $L$ , we define the intermediate generating functions $S^{L}(s+\mathfrak{c})(\unicode[STIX]{x1D709})$ by integrating an exponential function over all lattice slices of the affine cone 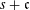 $s+\mathfrak{c}$ parallel to the subspace  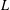$L$ and summing up the integrals. We expose the bidegree structure in parameters $s$ and 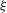$\unicode[STIX]{x1D709}$ , which was implicitly used in the algorithms in our papers [Computation of the highest coefficients of weighted Ehrhart quasi-polynomials of rational polyhedra. Found. Comput. Math.12 (2012), 435–469] and [Intermediate sums on polyhedra: computation and real Ehrhart theory. Mathematika59 (2013), 1–22]. The bidegree structure is key to a new proof for the Baldoni–Berline–Vergne approximation theorem for discrete generating functions [Local Euler–Maclaurin expansion of Barvinok valuations and Ehrhart coefficients of rational polytopes. Contemp. Math.452 (2008), 15–33], using the Fourier analysis with respect to the parameter  $s$ and a continuity argument. Our study also enables a forthcoming paper, in which we study intermediate sums over multi-parameter families of polytopes.

We study intermediate sums, interpolating between integrals and discrete sums, which were introduced by A. Barvinok in [Computing the Ehrhart quasi-polynomial of a rational simplex. Math. Comp. 75 (2006), 1449–1466]. For a given polytope 𝔭 with facets parallel to rational hyperplanes and a rational subspace L, we integrate a given polynomial function h over all lattice slices of the polytope 𝔭 parallel to the subspace L and sum up the integrals. We first develop an algorithmic theory of parametric intermediate generating functions. Then we study the Ehrhart theory of these intermediate sums, that is, the dependence of the result as a function of a dilation of the polytope. We provide an algorithm to compute the resulting Ehrhart quasi-polynomials in the form of explicit step-polynomials. These formulas are naturally valid for real (not just integer) dilations and thus provide a direct approach to real Ehrhart theory.

We realize the multiplihedron geometrically as the moduli space of stable quilted disks. This generalizes the geometric realization of the associahedron as the moduli space of stable disks. We show that this moduli space is the non-negative real part of a complex moduli space of stable scaled marked curves.

We recover the Newton diagram (modulo a natural ambiguity) from the link for any surface hypersurface singularity with non-degenerate Newton principal part whose link is a rational homology sphere. As a corollary, we show that the link determines the embedded topological type, the Milnor fibration, and the multiplicity of such a germ. This proves (an even stronger version of) Zariski's conjecture about the multiplicity for such a singularity.

Using multigraded Castelnuovo–Mumford regularity, we study the equations defining a projective embedding of a variety $X$. Given globally generated line bundles $B_{1}, \dotsc, B_{\ell}$ on $X$ and $m_{1}, \dotsc, m_{\ell} \in \mathbb{N}$, consider the line bundle $L := B_{1}^{m_{1}} \otimes \dotsb \otimes B_{\ell}^{m_{\ell}}$. We give conditions on the $m_{i}$ which guarantee that the ideal of $X$ in $\mathbb{P}(H^{0}(X,L)^{*})$ is generated by quadrics and that the first $p$ syzygies are linear. This yields new results on the syzygies of toric varieties and the normality of polytopes.

We introduce a new approach to the study of a system of algebraic equations in $(\mathbb{C}^\times)^n$ whose Newton polytopes have sufficiently general relative positions. Our method is based on the theory of Parshin's residues and tame symbols on toroidal varieties. It provides a uniform algebraic explanation of the recent result of Khovanskii on the product of the roots of such systems and the Gel'fond–Khovanskii result on the sum of the values of a Laurent polynomial over the roots of such systems, and extends them to the case of an algebraically closed field of arbitrary characteristic.