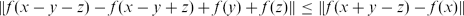1 results
ADDITIVE FUNCTIONAL INEQUALITIES AND DERIVATIONS ON HILBERT C*-MODULES
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 05 March 2013, pp. 341-348
- Print publication:
- May 2013
-
- Article
-
- You have access
- Export citation