Let
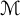 \mathcal {M}
be a semifinite von Nemann algebra equipped with an increasing filtration
\mathcal {M}
be a semifinite von Nemann algebra equipped with an increasing filtration
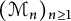 (\mathcal {M}_n)_{n\geq 1}
of (semifinite) von Neumann subalgebras of
(\mathcal {M}_n)_{n\geq 1}
of (semifinite) von Neumann subalgebras of
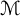 \mathcal {M}
. For
\mathcal {M}
. For
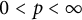 0<p <\infty
, let
0<p <\infty
, let
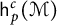 \mathsf {h}_p^c(\mathcal {M})
denote the noncommutative column conditioned martingale Hardy space and
\mathsf {h}_p^c(\mathcal {M})
denote the noncommutative column conditioned martingale Hardy space and
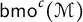 \mathsf {bmo}^c(\mathcal {M})
denote the column “little” martingale BMO space associated with the filtration
\mathsf {bmo}^c(\mathcal {M})
denote the column “little” martingale BMO space associated with the filtration
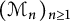 (\mathcal {M}_n)_{n\geq 1}
.
(\mathcal {M}_n)_{n\geq 1}
.
We prove the following real interpolation identity: if
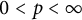 0<p <\infty
and
0<p <\infty
and
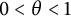 0<\theta <1
, then for
0<\theta <1
, then for
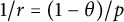 1/r=(1-\theta )/p
,
1/r=(1-\theta )/p
,
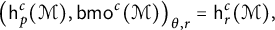 \begin{align*} \big(\mathsf{h}_p^c(\mathcal{M}), \mathsf{bmo}^c(\mathcal{M})\big)_{\theta, r}=\mathsf{h}_{r}^c(\mathcal{M}), \end{align*}
\begin{align*} \big(\mathsf{h}_p^c(\mathcal{M}), \mathsf{bmo}^c(\mathcal{M})\big)_{\theta, r}=\mathsf{h}_{r}^c(\mathcal{M}), \end{align*}
with equivalent quasi norms.
For the case of complex interpolation, we obtain that if
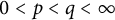 0<p<q<\infty
and
0<p<q<\infty
and
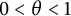 0<\theta <1
, then for
0<\theta <1
, then for
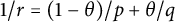 1/r =(1-\theta )/p +\theta /q
,
1/r =(1-\theta )/p +\theta /q
,
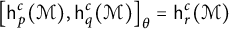 \begin{align*} \big[\mathsf{h}_p^c(\mathcal{M}), \mathsf{h}_q^c(\mathcal{M})\big]_{\theta}=\mathsf{h}_{r}^c(\mathcal{M}) \end{align*}
\begin{align*} \big[\mathsf{h}_p^c(\mathcal{M}), \mathsf{h}_q^c(\mathcal{M})\big]_{\theta}=\mathsf{h}_{r}^c(\mathcal{M}) \end{align*}
with equivalent quasi norms.
These extend previously known results from
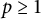 p\geq 1
to the full range
p\geq 1
to the full range
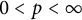 0<p<\infty
. Other related spaces such as spaces of adapted sequences and Junge’s noncommutative conditioned
0<p<\infty
. Other related spaces such as spaces of adapted sequences and Junge’s noncommutative conditioned
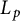 L_p
-spaces are also shown to form interpolation scale for the full range
L_p
-spaces are also shown to form interpolation scale for the full range
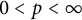 0<p<\infty
when either the real method or the complex method is used. Our method of proof is based on a new algebraic atomic decomposition for Orlicz space version of Junge’s noncommutative conditioned
0<p<\infty
when either the real method or the complex method is used. Our method of proof is based on a new algebraic atomic decomposition for Orlicz space version of Junge’s noncommutative conditioned
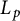 L_p
-spaces.
L_p
-spaces.
We apply these results to derive various inequalities for martingales in noncommutative symmetric quasi-Banach spaces.